TensorFlow实战——学习笔记（一）去噪自编码器实现

导入模块和数据

import numpy as np
import sklearn.preprocessing as prep
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

这里的自编码器采用Xavier initialization方法初始化参数，需要先定义好它。Xavier初始化器的特点是会根据某一层网络的输入、输出节点数量自动整合最合适的分布。使得初始化的权重不大不小，正好合适。从数学的角度分析，Xavier就是让权重满足0均值，同时方差为 2/(n[input] + n[output]),其中n为节点数，分布可以用均匀分布或高斯分布。
下面定义一个去噪自编码器的类，这个类包含构建函数init()和一些常用的成员函数。先看看构建函数init()。

init函数这样几个输入：n_input（输入变量数）、n_hidden（隐含层节点数）、transfer_function（隐含层激活函数，默认为softplus）、optimizer（优化器，默认为Adam）、scale（高斯噪音系数，默认为0.1）。其中，class中的scale参数做成了一个placeholder，参数初始化使用接下来定义的_initialize_weights函数。只使用一个隐含层。

class AdditiveGaussianNoiseAutoencoder(object):
    def __init__(self, n_input, n_hidden, transfer_function=tf.nn.softplus,
                 optimizer=tf.train.AdamOptimizer(), scale=0.1):
        self.n_input = n_input
        self.n_hidden = n_hidden
        self.transfer = transfer_function
        self.scale = tf.placeholder(tf.float32)
        self.training_scale = scale
        network_weights = self._initialize_weights()
        self.weights = network_weights

接下里开始定义网络结构，我们为输入x创建一个维度为n_input的placeholder。然后建立一个能提取特征的隐含层，先将x加上噪音，即 self.x+scale*tf.random_normal((n_input,)),然后用tf.mutmul将加了噪音的输入和隐含层的权重相乘，加上bias，最后使用transfer进行激活处理。经过隐含层后，我们要在输出层进行数据复原，重建操作（建立reconstruction层），这里不需要激活函数，直接将隐含层的s输出self.hidden乘以输出层的权重w2，加上bias2就好

        self.x = tf.placeholder(tf.float32, [None, self.n_input])
        self.hidden = self.transfer(tf.add(tf.matmul(self.x + scale * tf.random_normal((n_input,)),
                                                     self.weights["w1"]), self.weights["b1"]))
        self.reconstruction = tf.add(tf.matmul(self.hidden, self.weights["w2"]),
                                     self.weights["b2"])

接下来定义自编码器的损失函数，直接使用平方误差tf.subtract作为cost，计算输出self.reconstruction和输入self.x之间的差，再用tf.pow求差的平方，最后用tf.reduce_sum求和即可得到平方误差。在定义self.optimizer作为优化器对self.cost进行优化。最后创建Session，初始化自编码器全部模型参数

        self.cost = 0.5 * tf.reduce_sum(tf.pow(tf.subtract(self.reconstruction, self.x), 2.0))
        self.optimizer = optimizer.minimize(self.cost)

        init = tf.global_variables_initializer()
        self.sess = tf.Session()
        self.sess.run(init)

接下来看一下初始化权重的函数_initialize_weights先创建一个all_weights的字典，把w1，w2，b1,b2全部放进去，最后返回all_weights其中w1需要使用前面提到的xavier__init函数初始化，直接传入输入层节点数和隐含层节点数然后Xavier即可返回一个比较适合softplus扥激活函数的权重初始分布，b1直接用tf.zeros全部初始化为0。输出能self.reconstruction没有使用激活函数，直接w2和b2初始化为0即可。

    def _initialize_weights(self):
        all_weights = dict()
        all_weights["w1"] = tf.Variable(xavier_init(self.n_input, self.n_hidden))
        all_weights["b1"] = tf.Variable(tf.zeros([self.n_hidden], dtype=tf.float32))
        all_weights["w2"] = tf.Variable(tf.zeros([self.n_hidden, self.n_input], dtype=tf.float32))
        all_weights["b2"] = tf.Variable(tf.zeros([self.n_input], dtype=tf.float32))
        return all_weights

定义计算损失cost以及执行一步训练的函数partial_fit。函数里只需要让Session执行两个计算图的节点cost和optimizer，输入的feed_dict字典包括输出数据x和噪音系数scale。函数partial_fit做的就是用一个batch数据进行训练并返回当前的损失cost

    def partial_fit(self, X):
        cost, opt = self.sess.run((self.cost, self.optimizer),
                                  feed_dict={self.x: X,
                                             self.scale: self.training_scale})
        return cost

还需要定义一个只求损失cost的函数calc_total_cost，这里就只让Session执行一个计算图节点self.cost，传入的参数和前面的partial_fit一样。这个函数是自编码器训练完成后，在测试集上对模型性能进行评测的时候会用到的，不会像partial_fit触发训练操作

    def calc_total_cost(self, X):
        return self.sess.run(self.cost,
                             feed_dict={self.x: X, self.scale: self.training_scale})

定义transform函数，返回自编码器隐含层的输出结果。目的是提供一个借口来获取抽象后的特征，自编码器的隐含层的最主要功能就是学习数据中的高阶特征

    def transform(self, X):
        return self.sess.run(self.hidden,
                             feed_dict={self.x: X, self.scale: self.training_scale})

再定义generate函数。它将隐含层的输出结果作为输入，通过之后的重建层将提取到的高阶特征复原为原始数据。这个接口和前面的transform刚好将整个自编码器拆分为两部分，这里的generate为后部分，把高阶特征复原为原始数据的部分

    def generate(self, hidden=None):
        if hidden is None:
            hidden = np.random.normal(size=self.weights["w1"])
        return self.sess.run(self.reconstruction, feed_dict={self.hidden: hidden})

接下来定义reconstruct函数，它整体运行一遍复原过程

    def reconstruct(self, X):
        return self.sess.run(self.reconstruction,
                             feed_dict={self.x: X, self.scale: self.training_scale})

定义一个获取隐含层的权重w1的函数

    def get_weights(self):
        return self.sess.run(self.weights['w1'])

定义一个获取隐含层权重b1的函数

    def get_biases(self):
        return self.sess.run(self.weights["b1"])

定义一个对训练，测试数据进行标准化处理的函数。即让数据变成0均值，且标准差为1的分布方法就是先减去均值，再除以标准差。直接使用sklearn.preprocessing的StandardScaler这个类现在训练集上进行fit，在将这个Scaler用到训练数据和测试数据上。这里要注意的是，必须要保证训练集和测试集都使用相同的Scaler，这样才能保证后面处理数据的一致性。这也是为什么先在训练数据上fit出一个共用的Scaler的原因

def standard_scale(X_train, X_test):
    preprocessor = prep.StandardScaler().fit(X_train)
    X_train = preprocessor.transform(X_train)
    X_test = preprocessor.transform(X_test)
    return X_train, X_test

在定义一个随机获取block数据的函数：取一个0到batch_size之间的随机整数，再以这个整数作为block的起始位置，然后顺序得到一个batch_size数据。不放回抽样，提高数据的利用效率和随机性

def get_random_block_from_data(data, batch_size):
    start_index = np.random.randint(0, len(data) - batch_size)
    return data[start_index: (start_index + batch_size)]

def xavier_init(fan_in, fan_out, constant=1):
    low = -constant * np.sqrt(6.0 / (fan_in + fan_out))
    high = constant * np.sqrt(6.0 / (fan_in + fan_out))
    return tf.random_uniform((fan_in, fan_out),
                             minval=low, maxval=high,
                             dtype=tf.float32)

if __name__ == '__main__':
    # 加载数据
    mnist = input_data.read_data_sets('../datas/MNIST_data/', one_hot=True)
    # 对数据进行标准化变换
    X_train, X_test = standard_scale(mnist.train.images, mnist.test.images)
    # 定义几个常用参数：总训练样本数，最大训练轮数（epochs），batch_size，设置每隔一轮就显示一次损失cost
    n_samples = int(mnist.train.num_examples)
    training_epochs = 20
    batch_size = 128
    display_step = 1

    # 创建一个自编码器的实例，定义模型的输入节点n_input为784，自编码器的隐含层节点数n_hidden为200，隐含层激活函数为softplus，优化器为Adam且学习率为0.001，噪音系数scale设为0.01
    autoencoder = AdditiveGaussianNoiseAutoencoder(
        n_input=784,
        n_hidden=200,
        transfer_function=tf.nn.softplus,
        optimizer=tf.train.AdamOptimizer(learning_rate=0.001),
        scale=0.01
    )

    for epoch in range(training_epochs):
        avg_cost = 0.
        total_batch = int(n_samples / batch_size)
        for i in range(total_batch):
            batch_xs = get_random_block_from_data(X_train, batch_size)

            cost = autoencoder.partial_fit(batch_xs)
            avg_cost += cost / n_samples * batch_size

        if epoch % display_step == 0:
            print("Epoch: %04d" % (epoch + 1), "cost={:.9f}".format(avg_cost))

    print("Total cost:" + str(autoencoder.calc_total_cost(X_test)))

至此，去噪自编码器的TensorFlow实现就结束了。事实上，实现一个自编码器和实现一个单隐含层的神经网络差不多，只不过在数据输入的时候做了标准化，并加上了一个高斯噪音。同时我们的结果不是数字分类结果，而是复原的数据，因此不需要用标注过的数据进行监督学习。自编码器作为一种无监督学习，与其他无监督学习的区别是，它不对数据进行聚类，而是提取其中最有用，最频繁的特征，根据这些高阶特征重构数据。
这种思想可以先对数据进行预处理，提取到一些有用的特征，将神经网络权重初始化到一个较好的分布，然后再用有标注的数据进行监督学习，即对权重进行fine-tune。

实现过程中遇到的几个问题：

1、为什么要初始化参数？

2、tf.subtract函数的原理，还有tf.pow()

subtract(x ，y ，name=None)，向量减法
pow(x ，y ，name=None),计算x的y次方（mi）

3、为什么对训练，测试数据进行标准化处理

数据的标准化(normalization)是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值。
对原始数据进行标准化，使得每个变量有相同的范围或者方差

什么时候对数据中心化呢

1、在聚类过程中，标准化显得尤为重要。这是因为聚类操作依赖于对类间距离和类内聚类之间的衡量。如果一个变量的衡量标准高于其他变量，那么我们使用的任何衡量标准都将受到该变量的过度影响。

2、在PCA降维操作之前。在主成分PCA分析之前，对变量进行标准化至关重要。 这是因为PCA给那些方差较高的变量比那些方差非常小的变量赋予更多的权重。而 标准化原始数据会产生相同的方差，因此高权重不会分配给具有较高方差的变量

3、KNN操作，原因类似于kmeans聚类。由于KNN需要用欧式距离去度量。标准化会让变量之间起着相同的作用。

4、在SVM中，使用所有跟距离计算相关的的kernel都需要对数据进行标准化。

5、在选择岭回归和Lasso时候，标准化是必须的。原因是正则化是有偏估计，会对权重进行惩罚。在量纲不同的情况，正则化会带来更大的偏差。

4、上面的代码是怎么实现不放回抽样的

不明，待补充

5、tf.random_uniform的原理

random_uniform(
shape,
minval=0,
maxval=None,
dtype=tf.float32,
seed=None,
name=None
)
可以获取minval和maxval范围内的均匀分布随机值

6、为什么使用softplus

该解释来自引用https://www.zhihu.com/question/29021768
ReLu函数的全称为Rectified Linear Units，函数表达式为y=max(0,x)，softplus函数的数学表达式为y=log(1+e^x)，它们的函数表达式如下:

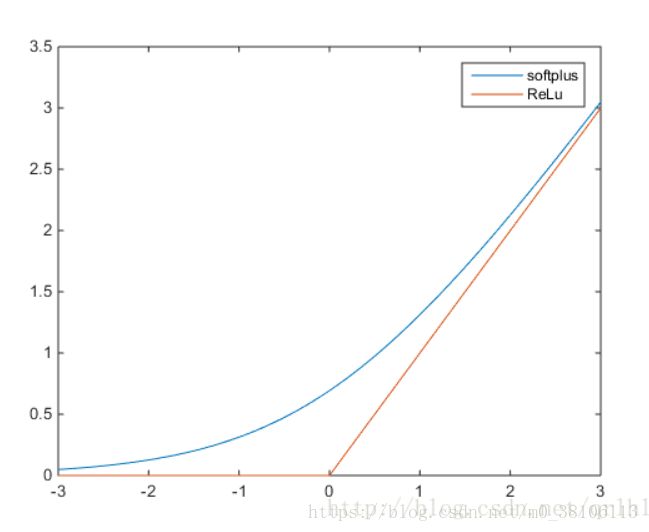
可以看到，softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，softplus和ReLu更加接近脑神经元的激活模型，而神经网络正是基于脑神经科学发展而来，这两个激活函数的应用促成了神经网络研究的新浪潮。
那么softplus和ReLu相比于Sigmoid的优点在哪里呢?
第一，采用sigmoid等函数，算激活函数时（指数运算），计算量大，反向传播求误差梯度时，求导涉及除法，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。
第二，对于深层网络，sigmoid函数反向传播时，很容易就会出现梯度消失的情况（在sigmoid接近饱和区时，变换太缓慢，导数趋于0，这种情况会造成信息丢失），从而无法完成深层网络的训练。
第三，Relu会使一部分神经元的输出为0，这样就造成了网络的稀疏性，并且减少了参数的相互依存关系，缓解了过拟合问题的发生（以及一些人的生物解释balabala）。