CS231N Assignment1 KNN

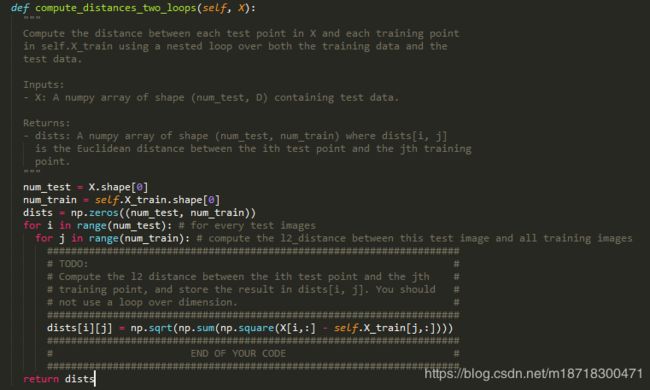
compute_distances_two_loops()

在上图的compute_distances_two_loops() 函数中，我们需要实现计算每张测试图像（如500张）与每张训练图像（如5000张）之间的L2距离，并返回一个500*5000的二维数组dists，dists[i,j]是第i张测试图像与第j张训练图像之间的L2距离

我们有L2距离的计算公式如下：

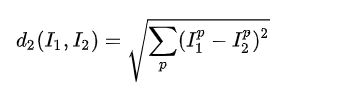
即两张图像的L2距离等于他们每个对应像素值之差的平方的累加值开根号

dists[i][j] = np.sqrt(np.sum(np.square(X[i,:] - self.X_train[j,:])))

对上图的计算语句，我们已知X是一个500 * 3072的数组，存储了500张32 * 32 * 3的测试图像
self.X_train是一个5000 * 3072的数组，存储了5000张32 * 32 * 3的训练图像
上述语句是在内层循环中，即已经由i指明了一张测试图像，以及j指明了一张训练图像，我们用这个语句计算测试图像i与训练图像j之间的L2距离并将计算结果存储在dists[i,j]中

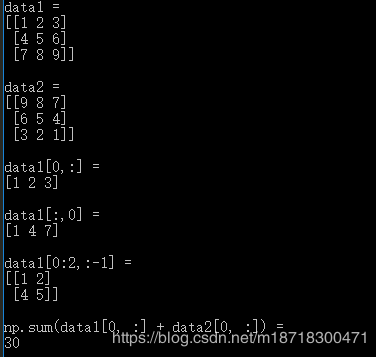
ArraySlicing

要理解这个语句，我们首先要知道python中的数组切分Array Slicing，符号为 冒号 ：

一维数组中的切分
data[:] 输出data中所有元素
data[start:end] 输出data中下标【start，end-1】的元素
若冒号的左边/右边没有指明数字下标，则取各自的界限值，即左边补0/右边补（数组长度-1）
又python中的负数下标-x理解为（长度-x），故有
data[:-1] 为输出data中下标【0,（长度 - 1）- 1】的元素

二维数组中的切分
可由一维数组中的切分拓展而得

上图中

np.sum(data1[0, :] + data2[0, :]) 

所做的事情是（（1+9） + （2+8） + （3+7））
由此可见，只要公式中出现了求和符号∑，就可以调用np.sum()函数进行计算

---

predict_labels()

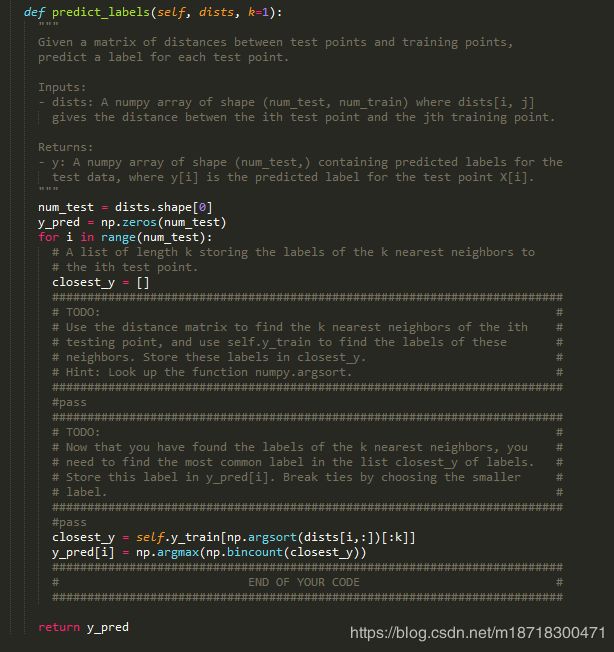
predict_labels() 函数中我们需要实现由测试图像与训练图像间的距离来预测测试图像的标签
该函数的输入是二维数组dists 其中dist[i, j]是我们之前计算出的测试图像i与训练图像j的L2距离
当k=1时，我们取与测试图像i距离最近的训练图像j的标签作为测试图像i的标签；
当k=N时，我们取最近的N个训练图像，并取这N个最近的训练图像中的最多的标签作为测试图像的标签

closest_y 是训练图像标签数组y_train的一个子数组，对每个测试图像i，根据以下语句获得这个子数组

closest_y = self.y_train[np.argsort(dists[i,:])[:k]] 

其中np.argsort() 函数完成的功能是以某种算法对数组进行从小到大排序，并返回一个存储有排序结果的下标的数组
例如：

返回的下标数组是[2 3 1 0]，说明下标2的元素（0.0）最小，下标3的元素（0.1）次小，下标0的元素（1.48）最大

故原语句实现的是对dists[i,:] 这个数组进行排序，返回了下标数组，截取这个下标数组的前k个值，用来获得y_train的子数组
将这一语句扩展写开以便更好理解

subscripts = np.argsort(dists[i,:]) # 对dists[i,:]排序获得下标数组
FirstKs = subscripts[:k] # 切分下标数组，获取其前K个元素
closest_y = self.y_train[FirstKs] # 将前K个最小下标所对应的训练图像标签存储到closets_y中

最后，我们通过下面这个语句预测测试图像i的标签

y_pred[i] = np.argmax(np.bincount(closest_y))

np.bincount() 的返回值是一个长度为（数组中最大值+1）的数组，所做的事情是对数组做一个类似桶排序的处理，即数组中的元素每出现一次，其对应索引位置的值就加1
如

数组中最大值为7，故返回一个长度为8的数组，
数组中元素0出现了1次，故返回的数组中索引0的值是1，
数组中元素1出现了3次，故返回的数组中索引1的值是3，
数组中元素7出现了1次，故返回的数组中索引7的值是1

np.argmax() 返回数组中最大元素的下标

故原语句所做的事情是：

1. 通过np.bincount(closest_y)统计closest_y中每个标签出现的次数
2. 找出出现次数最多的标签并赋给y_pred[i]作为我们对测试图像i的预测标签

---

compute_distances_one_loop()

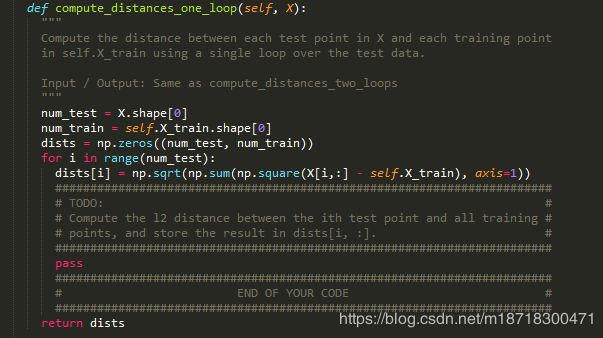
在这个函数中我们需要实现只使用一个循环就完成图像间的L2距离计算，这就涉及到了numpy的广播机制
（广播机制的规则详见 https://zhuanlan.zhihu.com/p/33318510）

这里我们具体来理解一下上述语句中的广播机制是如何运行的

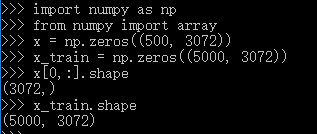
上述代码中，我们初始化了500 * 3072的数组x与5000 * 3072的数组x_train，并可见x[0,:]是长3072的一维数组

X[i,:] - self.X_train

因为x[0,:]是长3072的一维数组，而x_train是5000 * 3072的数组，我们知道上述计算语句是应用了广播才能正确计算出来的
根据广播机制的规则，我们知道其处理过程如下：

1. 如果两个数组维数不相等，维数较低的数组的shape会从左开始填充1，直到和高维数组的维数匹配
   X[i,:] 与self.X_train 的维数不相等，故维数较低者X[i,:] 会从左开始填充1，填充后变为(1, 3072)
2. 如果两个数组维数相同，但某些维度的长度不同，那么长度为1的维度会被扩展，和另一数组的同维度的长度匹配
   现在两数组维数相同，但维度长度不同，故长度为1的维度被拓展，X[i,:] 拓展为(5000, 3072)
3. 如果两个数组维数相同，但有任一维度的长度不同且不为1，则报错
   此处无此情况发生

经过上述广播后，X[i,:] 最终成为了5000*3072的数组，与self.X_train完全匹配，可以进行对应位的相减后平方运算
通俗来说就是将X[i,:] 这个长3072的数组使用了5000次去与5000张不同的测试图像进行距离计算，因为利用了广播机制而不是双重循环，算法得到了优化

---

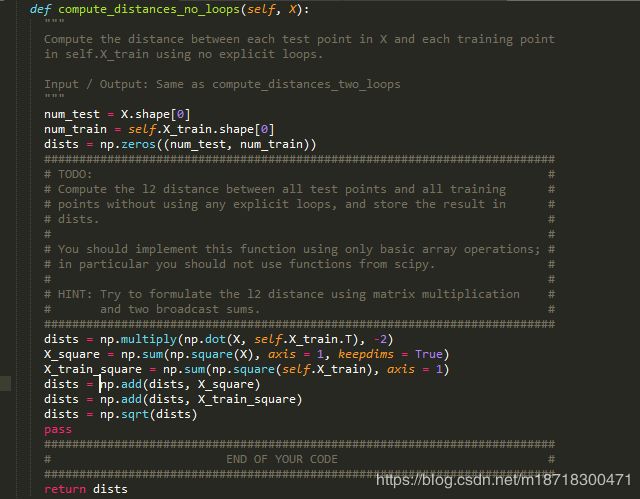
compute_distances_no_loops(）

将L2计算公式开平方并分配求和符号
$$\begin{gathered} L2=\sqrt{\sum _{i=0}^{3071}(p1[i]-p2[i]{)}^2} \\ =\sqrt{\sum _{i=0}^{3071}((p1[i]{)}^2+(p2[i]{)}^2-2\ast p1[i]\ast p2[i])} \\ =\sqrt{\sum _{i=0}^{3071}(p1[i]{)}^2+\sum _{i=0}^{3071}(p2[i]{)}^2-\sum _{i=0}^{3071}(2\ast p1[i]\ast p2[i])} \end{gathered}$$

在计算之前再理顺一下各个变量的意义
X ： 500*3072的数组，存储了500张测试图像，X[i]是一个长3072的数组（一个行向量），是第i张图像的全3072个像素
self.X_train ： 5000 * 3072的数组，存储了5000张测试图像，self.X_train[i]同理
dists ： 500 * 5000的数组，dists[i]是长5000的数组，是第i张测试图像与所有5000张训练图像的L2距离，dsts[i][j]是第i张训练图像与第j张测试图像的距离

${\sum }_{i=0}^{3071}(p1[i]{)}^2$的计算：

X_square = np.sum(np.square(X), axis = 1, keepdims = True) # X_square.shape = (500, 1)

上述语句的执行过程分析如下：

1. np.square(X)将X按元素平方，得到500 * 3072的数组，数组中元素值为原来的平方
2. X_square = np.sum(np.square(X), axis = 1, keepdims = True) 将np.square(X)这个500 * 3072的数组在axis = 1的前提下进行累加并因为 keepdims 参数为True而保持维度，得到一个长500 * 1的数组（一个列向量），该数组元素 X_square[i][0] 就是${\sum }_{i=0}^{3071}(p1[i]{)}^2$

同理，由以下语句求得${\sum }_{i=0}^{3071}(p2[i]{)}^2$

X_train_square = np.sum(np.square(X_train), axis = 1) # X_train_square.shape = (5000, )

此处我们没有将 keepdims 参数设为真，故得到一个长5000的一维数组，且 X_train_square[i] 就是${\sum }_{i=0}^{3071}(p2[i]{)}^2$

最后我们需要计算${\sum }_{i=0}^{3071}(2\ast p1[i]\ast p2[i])$,可见该运算完成了[0…3071]对应元素相乘的二倍的累加

dists = np.multiply(np.dot(X, self.X_train.T), -2) #dists.shape = (500, 5000)

上述语句执行过程如下：

1. self.X_train.T是self.X_train的转置，self.X_train是5000 * 3072的数组，故转置后为3072 * 5000
2. np.dot(X, self.X_train.T)完成X（500 * 3072）与self.X_train.T（3072 * 5000）的矩阵乘法，结果为500 * 5000的数组，据矩阵相乘，结果为对应像素相乘后累加，即${\sum }_{i=0}^{3071}(p1[i]\ast p2[i])$
3. 最后乘以-2得到结果

综上得如下代码段

其中广播机制在两个np.add()时发挥了作用

dists = np.add(dists, X_square)

X_square.shape = (500, 1)，计算时因广播机制而扩展为(500, 5000)，即复制了5000列X_square加到dists中，其意义是将500张测试图像算出的${\sum }_{i=0}^{3071}(p1[i]{)}^2$加到5000张测试图像中

dists = np.add(dists, X_train_square)

X_train_square.shape = (5000, )，计算时因广播机制扩展为(1,5000)后再扩展为(500,5000)，即复制了500行X_train_square，其意义是将5000张训练图像算出的${\sum }_{i=0}^{3071}(p2[i]{)}^2$加到500张测试图像中

---

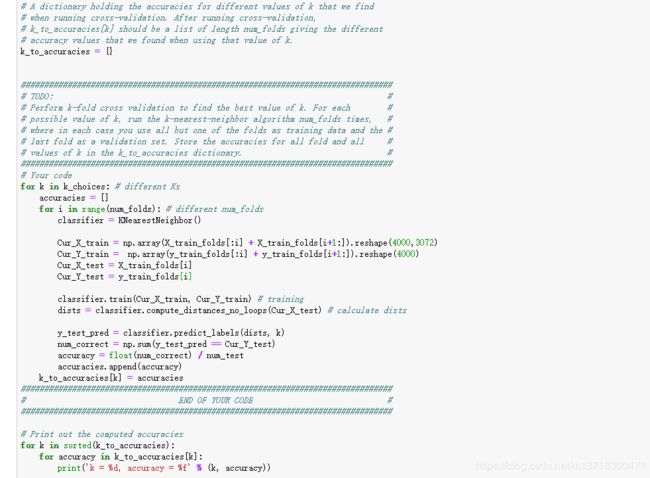
交叉验证

将训练集（包括训练图像X_train与对应的标签y_train）分成num_folds等分，利用np.array_split()

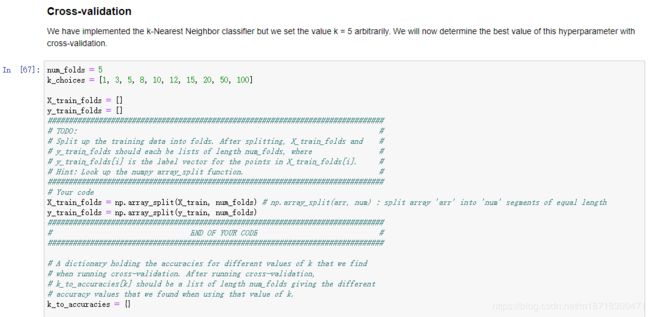
对不同的K值进行交叉验证，在之前分好的num_folds等分的训练集中，选取一等分作为验证集，其余四等分作为训练集，训练分类器并进行预测后统计预测的准确度

---

关于axis的扩展阅读：https://zhuanlan.zhihu.com/p/30960190