线性回归 (linear regression model) 原理与代码实现
这篇博文是在总结网易公开课上ng的机器学习第二讲和周志华老师书上线性回归的个人总结。准备做一个系列笔记,希望能坚持。
代码放在文后
什么是线性模型
通俗一点来讲,就是我们希望用一个线性组合,来拟合我们的数据,实质上是求解输入到输出的一个线性函数的映射。当然非线性映射也是有的,比如对数线性回归。线性模型一半是监督学习。本文中讲的线性回归模型就是的。
线性模型可以干什么呢?线性模型有常见的线性回归,对数回归等等,他们可以用在数据的预测上,逻辑回归可以用在分类上。
线性模型的一般表达式:
线性回归模型
首先解释一下“回归”二字的意思,周志华老师在其书《机器学习》(下文用“书中”代指)中讲到:若预测的值是离散的,例如好人,坏人;得病,不得病,这种称为分类(classification);如预测的是连续值,我们称之为回归(regression)。显然线性问题是一个连续的,所以我们称之为线性回归(正误可以勘正)。
线性回归假定给定数据集D = {(x1,y1),(x2,y2)...,(xn,yn)},线性回归试图学习一个线性模型尽可能的预测实际值的输出。我们用h表示模型的预测输出值。那么h的表达式如下:

用向量表示就是我们常见的形式:
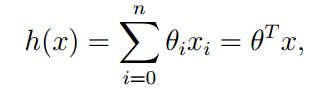
其中x1,x2…xn是我们的样本数据,x1表示x1这个特征,h(x)表示预测函数(hypotheses h)theta表示每一个特征的权重,注意theta0是线性函数的纵截距,x0 = 1. n表示输入特征的个数.
在这个模型中。w是未知的,我们称之为参数。线性回归的模型求解就是计算出theta。
回想一下,我们的h是一个假设值,真是的函数值是y,我们的目标是想用假设的y来代替y,所以我们的目标其实是如何让h最大限度的趋近与y。为了达到这个目的,我们定义了个一个称之为损失函数的函数(cost function)定于如下:
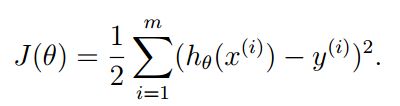
此时,我们的目标是如何让j最小。以达到全局最优的解。让我们好好看看这个cost function,它的sigma里面其实是一个最小二乘(least squares)。所以,线性回归模型中求解最优值的过程中,使用到了最小二乘算法来进行参数估计。在线性回归中,最小二乘就是试图找到一条直线,是的所有样本到直线上的欧氏距离之和最小。下面我们来看看如何求的在J取得最小值的时候h的取值,间接的也就求出了theta的值。
为了求解,我们采用梯度下降算法来描述这个过程。选定初始的w,然后不断的进行学习更新w,达到最优的解
更新规则如下:

这里的alpha 称为学习率。
我们推导偏导数考虑值只对一个样本,偏导数如下:

将其带入到公式()中,得到一次更新规则如下:
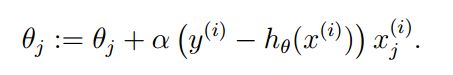
那么对于所有的样本,有如下算法:
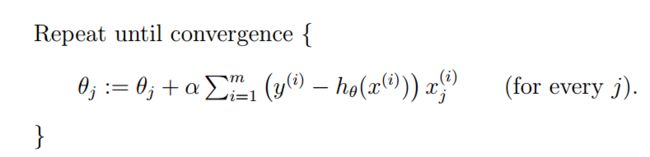
上面这个方法被称为batch gradent descent的线性回归问题求解。我们看到其每次循环需要对所有的样本进行计算(sigma)如果样本很大的时候,那么计算的次数将会很大,所以这个算法并不适合大样本的学习。
为了使其能在大样本下依旧完美工作,将算法进行改进:

这个算法的称之为stochastic gradient descent(incremental gradient descent).
还有一个用矩阵来求解的过程,具体就不写了,直接给出结果
声明:公式来自NG的讲义
实现
笔者用java实现了三种geadient descent 算法, 代码如下:
package com.dmml.linear;
/**
* Created by macan on 2016/10/12.
*/
import java.util.ArrayList;
/**
* 梯度下降算法求解线性回归模型
* 1. batch gradient descent
* 2. stochastic gradient descent
* 3. gradient descent by matrix
*
* 假设: 特殊是N维的, 结果是一维的
*
*/
public class GradientDescent {
public final static int maxIterator = 1000;
/**
* 学习data set
*/
private ArrayList<int[]> trainData;
/**
*
*/
private ArrayList targetData;
/**
* learning rate
*/
private static double alpha = 0.00001;
/**
* 特征的维度
*/
private int N;
/**
* 样本的个数
*/
private int M;
/**
* theta 参数
* double
*/
private double[] theta;
/**
* 构造方法
* @param trainData 训练数据集
* @param testData 测试数据集
*/
public GradientDescent(ArrayList<int[]> trainData, ArrayList testData){
this.trainData = trainData;
this.targetData = testData;
M = trainData.size();
N = trainData.get(1).length;
//初始化theta
theta = new double[N];
}
/**
* batch gradient descent algorithm
*/
public void batchGradientDescent(){
//计算
//迭代,设置最大的迭代次数为1000
for (int n = 0; n < maxIterator; ++n) {
for (int i = 0; i < N; ++i){
double temp = batchOndGradient(i);
if (temp <0.001){
break;
}
theta[i] += temp;
}
}
}
/**
* stochastic gradient descent
*/
public void stochasticGradientDescent(){
//计算
//迭代,设置最大的迭代次数为1000
for (int n = 0; n < maxIterator; ++n) {
//for each feature
for (int i = 0; i < N; ++i){
//for each row data
for (int m = 0; m < M; ++m) {
theta[i] += stochasticOneGradient(m,i);
}
}
}
}
/**
* 利用矩阵的思路,来解决gradient descent
*/
public void matrixInGradientDescet(){
double[][] train = toArray(trainData);
double[][] target = toArray2(targetData);
double[][] x1 = Matrix.trans(train);
//计算
double[][] res = Matrix.times(Matrix.times(Matrix.inv(Matrix.times(x1, train)), x1), target);
for (int i = 0; i < res.length; ++i){
for (int j = 0; j /**
* 计算sigma(y - h(x))x(i,j)
* @param f 特征index
* @return 返回计算的结果
*/
public double batchOndGradient(int f) {
double result = 0.0;
double temp = 0.0;
for (int m = 0; m < M; ++m) {
//计算h(x)
double hx = 0.0;
int[] X = trainData.get(m);
for (int i = 0; i < N; ++i) {
hx += theta[i] * X[i];
}
//计算(h - hx) * x
temp += (targetData.get(m) - hx) * X[f];
}
return alpha * temp;
}
public double stochasticOneGradient(int m, int f){
double result = 0.0;
double temp = 0.0;
//计算h(x)
double hx = 0.0;
int[] X = trainData.get(m);
for (int i = 0; i < N; ++i) {
hx += theta[i] * X[i];
}
//计算(h - hx) * x
return alpha * ((targetData.get(m) - hx) * X[f]);
}
public static double[][] toArray(ArrayList<int[]> data){
double[][] res = new double[data.size()][data.get(1).length];
for (int i = 0;i < data.size(); ++i){
for (int j = 0; j < data.get(i).length; ++j){
res[i][j] = (double)data.get(i)[j];
}
}
return res;
}
public static double[][] toArray2(ArrayList data){
double[][] res = new double[data.size()][1];
for (int i = 0;i < data.size(); ++i){
res[i][0] = data.get(i).doubleValue();
}
return res;
}
public void print(){
for (int i = 0; i < theta.length; ++i){
System.out.print("theta" + i + " = " + theta[i]);
}
System.out.println();
}
public void initTheta(){
for (int i = 0; i < N; ++i){
theta[i] = 0.0;
}
}
public double[] getTheta(){
return theta;
}
}
测试代码:
@Test
public void testGradientDescent(){
int N = 4;
int M = 300;
ArrayList<int[]> data = createDataSet(N, M);
ArrayList<int[]> train = new ArrayList<int[]>();
ArrayList test = new ArrayList();
for (int[] sub : data){
int[] t = new int[N];
for (int i = 0; i < N; ++i){
t[i] = sub[i];
}
train.add(t);
test.add(new Integer(sub[N]));
}
//System.out.println(data);
GradientDescent gradientDescent = new GradientDescent(train, test);
System.out.println("batch Gradient descent...");
gradientDescent.batchGradientDescent();
gradientDescent.print();
double[] th1 = gradientDescent.getTheta();
System.out.println("stochastic Gradient Descent");
GradientDescent sgd = new GradientDescent(train, test);
sgd.stochasticGradientDescent();
sgd.print();
double th2[] = sgd.getTheta();
System.out.println("matrix In Gradient Descet");
GradientDescent mgd = new GradientDescent(train, test);
mgd.matrixInGradientDescet();
mgd.print();
double[] th3 = mgd.getTheta();
saveData(data, th1, th2, th3);
}
public void saveData(ArrayList<int[]> data, double[] th1, double[] th2, double[] th3)
{
String path = "data.txt";
try {
BufferedWriter writer = new BufferedWriter(new FileWriter(new File(path)));
for (int[] rows : data){
for (int i = 0; i< rows.length; ++i){
writer.write(rows[i] + "\t");
}
writer.write("\n");
}
for (int i = 0; i < th1.length; ++i){
writer.write("theta" + i + " = " + th1[i] + "\t");
}
writer.write("\n");
for (int i = 0; i < th2.length; ++i){
writer.write("theta" + i + " = " + th2[i] + "\t");
}
writer.write("\n");
for (int i = 0; i < th3.length; ++i){
writer.write("theta" + i + " = " + th3[i] + "\t");
}
writer.write("\n");
writer.close();
} catch (IOException e) {
e.printStackTrace();
}
} 用矩阵这种运算的时候,截距算的很大,这个原因我也不知道为啥,如果用童鞋看出来,请指教。

