ResNeXt-2017
- 论文链接:https://arxiv.org/pdf/1611.05431.pdf
- 论文题目:Aggregated Residual Transformations for Deep Neural Networks
ResNeXt
Abstract
我们提出一种用于图像分类的简单的,高度结构化的网络结构。我们的结构是通过重复一个构建单元来完成的,这个构建单元是一系列拥有同样拓扑结构的变换的聚合。我们这个简单的设计最终会形成一个均匀的同分支结构,这个结构只需要设定很少的超参数。这个策略开发了除了深度和广度的一个新的维度,我们叫做 cardinality(变换集合的大小)。在 ImageNet-1K 数据集上,在保证复杂度的条件下,我们提高 cardinality,分类准确率会提高。而且,当我们想要增加容量的时候,增加 cardinality 会比加深网络或者加宽网络来得更高效。我们的模型叫做 ResNeXt。
1. Introduction
关于视觉识别的研究正在经历从“特征工程”到“网络工程”的转变。相比于传统的人工设计的特征(如SIFT和HOG),在训练过程中,通过神经网络从大量数据中学习到的特征会引入非常少的人工干预,这使得学习到的特征可以转移到各种各样的识别任务中去应用。这样人类的工作重心就转移了设计更好的网络结构来学习特征。
设计结果会随着超参数(广度,卷积核大小,步长等)的增加变得非常困难,尤其当有很多层的时候。VGG-nets提出一种简单且有效的构建深度网络的策略:相同大小单元的堆叠。ResNets正是继承了这样的特点,用相同结构的模块进行堆叠。这个简单的规则减少了超参数的个数,然后深度被认为是神经网络的一个非常重要的维度。并且,这个策略的简单性也降低了对于特定数据集,选择出的超参数的过拟合的风险。VGG-nets和ResNets的鲁棒性在各种各样任务上都得到了体现,它们可以应用于视觉任务以及非视觉任务,如语音和语言学习。
不像VGG-nets,Inceptions模块族证明了精心设计的结构会在理论上更加低的复杂度上取得与之相匹配的效果。Inceptions模块随着时间在不断进化,但是始终保留了一个很重要的特点就是使用 split-transform-merge 的策略(也就是先拆分再变换再合并)。在一个Inception模块中,输入通过1x1的卷积被划分到一些低维的嵌入表达中,然后再通过特定的滤波器(如3x3,5x5),然后再通过拼接合并起来。Inception的这一策略被认为是构建具有强力表达能力的大且密集的层,同时计算复杂度还相对低的一种方法。
尽管取得了很好的准确率,但是Inception模块的实现还是比较复杂的,因为它涉及到很多复杂的因素,如卷积核数,还有对应每个变换的卷积核大小,还有模块结构都是需要根据每个stage来进行设计的。尽管通过精心设计,这些模块的结合会得到一个非常好的神经网络,但是对于新的任务/新的数据集,我们不一定清楚要怎么来设计Inception结构,尤其是在这么多超参数的情况下。
那么本文就提出一种简单的结构,并且以一种简单并且可延伸的方式同时采用了VGG/ResNets中的重复层的结构和Inceptions模块中的拆分变换合并的策略。我们网络的模块在每个低维嵌入上实施一系列变换然后再将输出通过相加的方式聚合。我们追求一种简单的实现这一思想的方法,也就是聚合的每个变换都是同样的结构,如图1右。这个设计允许我们延伸出任意数量的变换且不需要特别的设计。

图1. 左:ResNet的一个单元。右:ResNeXt中cardinality为32的一个单元,有着大致相同的复杂度。
有趣的是,在同样的情况下,我们的模型有两种不同的等价形式(如图三)。图三(b)的重构和Inception-ResNet模块一样是通过多路拼接,但是我们的模块不同于现在的所有的Inception模块的就是我们每一条路都享有同样的结构,因此我们可以轻松地将path的数量作为一个需要研究的因素剥离开来。更加简洁的一种重构就是图三(c),使用群卷积,这只是工程上的一种实现而已。

图3. ResNeXt的等价构建单元。(a)如图1右的聚合残差变换。(b)和(a)等价的模块,通过提前的拼接。(c)和(a,b)等价的单元,通过群卷积。图中加粗的文本表示重构。
通过实验,我们展示了我们的聚合变换比原来的ResNet模块有更好的效果,即使在同样的计算复杂度和模型大小上。如图1右就是设计来保持与图1左有着同样的FLOPs复杂度和参数个数。需要强调的是,通过增加容量来提高准确率是相对容易的,但是在保持复杂度的情况下提高准确率在现有文献中是非常少见的。
我们的方法表明 cardinality 是一个除了宽高之外的具体的可以量化的重要维度。实验表明增加 cardinality 是相比于增加广度高度更为有效的提高准确率的方法,尤其是在现有的模型下当高度广度带来回馈很小的情况下。
我们的神经网络,叫做 ResNeXt (暗示了 next 维度,也就是多一维度),在ImageNet分类数据集上性能超过ResNet-101/152,ResNet
-200,Inception-v3和Inception-ResNet-v2。尤其是,101层ResNeXt能够在仅用ResNet-200一般复杂度的情况下超过ResNet-200的准确率。而且,ResNeXt有着比所有Inception模型都有简单的设计思路。
2. Relatd Work
Multi-branch convolutional networks. Inception模型成功运用了多分支结构,每个分支都需要仔细的构建。ResNets也可以被视为是一个二分支网络,其中一个分支是恒等映射。深度神经决策树也是一个学习分割函数的树状的多分支网络。
Grouped convolutions. 群卷积的使用可以追溯到AlexNet。来源于Krizhevsky提出的将模型分布在两个GPU上。Caffe,Torch以及其他一些框架都支持群卷积,主要是为了AlexNet。据我们所知,很少人研究利用群卷积来提高准确率。一个极端的群卷积例子就是Channel-wise卷积,也就是groups的数量等于通道数。Channel-wise卷积是分离卷积的一部分。
Compressing convolutional networks. 网络结构分解(在特征图层级或者通道层级)是一种广泛被采用的减少深度网络冗余的技术,可以由此来压缩和加速网络。Ioannou等人提出的“root”-patterned网络来减少计算量,root的分支是经过群卷积的。这些方法都展示了在较低复杂度和较小的模型下取得不错的准确率。我们的方法并不是旨在压缩网络,而是一种能够展现更强特征表现力的网络结构。
Ensembling. 对多个独立的经过训练的网络取平均是一种有效的提高准确率的方法,该方法被大量运用于识别任务竞赛中。Veit等人将一个单独的ResNet解释为一个很多浅层网络的集成,这来自于ResNet网络的加法效应。我们的方法利用加法来聚合一系列的变换,但是我们认为将我们的方法理解为集成也是不准确的,因为我们所要集成的东西是一起训练的,而不是分开单独训练出来的。
3. Method
3.1. Template
我们效仿VGG/ResNets采用高度模块化的设计。我们的网络由残差模块堆叠而成。这些模块拥有同样的拓扑结构,并且服从两个简单规则:i)如果生成同样大小的特征图,模块共享超参(广度和卷积核大小),ii)每次当特征图进行了因子为2的降采样,那么模块的广度就乘2。第二个规则保证了计算复杂度,对于FLOPs(浮点数运算,包括乘加),几乎所有的模块都是相同的。
有了这两个规则,我们只需要设计一个模板模块就行了,然后网络里面的所有模块都可以根据模板来定义。所以这两条规则大大降低了需要设计的超参,并且能够让我们着眼于这些关键因素上。通过这些规则建立的网络在表1。
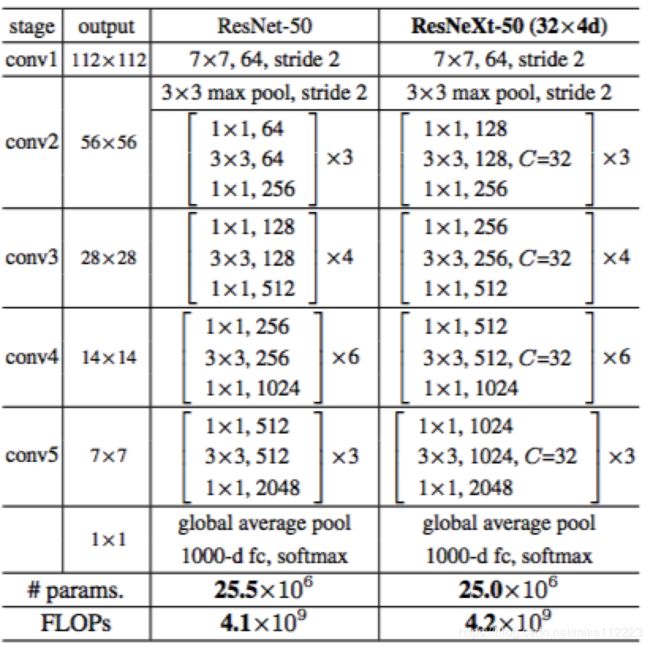
表1. (左)ResNet-50。(右)带有32x4d模板(采用图3c的结构)的ResNeXt-50。括号内是残差模块的形状,括号外是该stage上堆叠的模块个数。“C=32”表示使用group为32的群卷积。左右两个模型在参数个数和FLOPs都是相似的,也就是量级相同。
3.2. Revisiting Simple Neurons
神经网络中最简单的神经元是完成内积的(也就是加权求和),它是通过全连接层和卷积层完成的基础变换。内积可以被认为是集成变换的一种形式:
(1) ∑ i = 1 D w i x i \sum_{i=1}^Dw_ix_i \tag1 i=1∑Dwixi(1)
这里 x = [ x 1 , x 2 , . . . , x D ] \mathbf{x} = [x_1,x_2,...,x_D] x=[x1,x2,...,xD]是一个输入到神经元的D通道的输入向量, w i w_i wi是对应第i个通道的卷积核的权重。这个操作(通常还包括后续的一个输出的非线性)被视作为一个“神经元”,如图2。
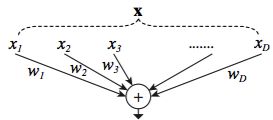
图2. 一个完成内积的简单神经元。
上述的操作可以被重塑为一个切分,变换再聚合的过程的结合。i)Splitting:将向量 x \mathbf{x} x切片为一个个低维嵌入,就像上面提到的,是一个单维子空间 x i x_i xi。ii)Transforming:每个低维特征表达都经过了变换,如上经过简单的缩放: w i x i w_ix_i wixi。iii)Aggregating:所有经过变换的嵌入最后通过相加聚合起来。
3.3. Aggregated Transformations
经过上面对于一个简单神经元的分析,我们考虑将基础变换( w i x i w_ix_i wixi)替换为一个更为一般性的方程,甚至它自己也可以是一个网络。不同于"Network-in-Network"是为了增加网络深度,我们的"Network-in-Neuron"是延伸为一个新的维度。
形式上,我们将整个变换过程表示为:
(2) F ( x ) = ∑ i = 1 C T i ( x ) , \mathcal F(\mathbf x)=\sum_{i=1}^C \mathcal T_i(\mathbf x), \tag 2 F(x)=i=1∑CTi(x),(2)
这里 T i ( x ) \mathcal T_i(\mathbf x) Ti(x)可以是任意函数。类似于一个简单神经元, T i \mathcal T_i Ti可以将 x \mathbf x x映射到嵌入(一般是低维)中然后变换它。
在方程2中, C C C是需要聚合的变换的组数。我们将 C C C定义为 cardinality 。方程2中的 C C C在位置上是与方程1中的 D D D是相似的,但是 C C C并不等于 D D D,它可以是任意数字。广度这一维度是和简单变换的数量有关的(内积),然而 cardinality 这一维度是和更为复杂的变换相联系的。我们通过实验发现 cardinality 是一个很重要的维度,而且它比深度广度更为有效。
在这篇论文中,我们考虑一种简单的方法来设计变换函数:所有的 T i \mathcal T_i Ti拥有同样的结构。这延续了VGG风格的策略,相同大小层的重复,这有助于剥离出少数超参,而且可以任意延展。我们定义 T i \mathcal T_i Ti为一个瓶颈结构,如图1右。每个 T i \mathcal T_i Ti的第一个 1 × 1 1 \times 1 1×1层是用于生成低维嵌入。
变换方程2变为下面的残差方程:
(3) y = x + ∑ i = 1 C T i ( x ) , \mathbf y=\mathbf x + \sum_{i=1}^C \mathcal T_i(\mathbf x), \tag 3 y=x+i=1∑CTi(x),(3)
这里 y \mathbf y y是输出。
Relation to Inception-ResNet. 在tensor的操作中图1右模块和图3b模块是等价的。图3b看起来和Inception-ResNet模块很相似,因为它包含了多个分支和拼接。但是和所有的Inception不同的是,我们多条分支上的模块是共享结构的。我们只需要设计一条分支就可以了。
Relation to Grouped Convolutions. 如果使用群卷积的概念的话,那么上述的模块将会更加简洁,如图3c。所有的低维嵌入层(第一层的 1 × 1 1 \times 1 1×1卷积层)可以被一个更宽的单一卷积层来代替(如图3c,128通道的 1 × 1 1 \times 1 1×1卷积)。切分是通过群卷积来完成的,它会将输入通道平均分入group中。如图3c的群卷积层就是进行32个组别的卷积,对应的输入输出分别是4通道。经过分组别卷积之后,群卷积层会将输出拼接起来再输出。图3c中的模块就和图1左的残差模块长得很相似了,只是图3c的模块是一个更广但是稀疏连接的模块。
我们注意到只有当模块的深度大于3层的时候,重构才会有意义,如果深度为2,重构只会单纯延伸出一个更广更密集的模块,如图4。

图4. (左):深度为2的Aggregated Transformations,(右)等效模块,只是单纯变宽了(通道变多)。
Discussion. 我们注意到尽管我们利用拼接,群卷积来更好的完成重构,但是这样的重构并不适用于一般性的方程3。例如,如果 T i \mathcal T_i Ti可以采用任意形式而且每个分支不同。我们选择使用同样形式是因为它更加简单且具有延展性。在这样简单的设定下,群卷积会有很大帮助。
3.3. Model Capacity
下一个部分,通过实验我们验证了在保持模型复杂度和参数个数的情况下,我们的模型提高了准确率。这不仅仅具有实际意义,更重要的是,模型的复杂度和参数个数代表了模型的固有的容量,因此这更有助于我们研究深度网络的本质特性。
当我们在评估不同 cardinality C 的时候,我们有意识的保持网络的复杂度,我们想要最小化对于其他超参数的修改。我们选择调整瓶颈结构的宽度(如图1右的4d),因为它是独立于模块输入和输出的。这个策略不会引入对于别的超参数的修改(模块的输入输出的深度和宽度),所以会有助于我们研究 cardinality 的影响。
图1左,原始的ResNet瓶颈结构大约有 256 ∗ 64 + 3 ∗ 3 ∗ 64 ∗ 64 + 256 ∗ 64 ≈ 70 k 256*64+3*3*64*64+256*64 \approx 70k 256∗64+3∗3∗64∗64+256∗64≈70k以及等比的FLOPs(对于同样的特征图大小)。对于带有广度d瓶颈结构的我们的模板,图1右拥有:
(4) C ⋅ ( 256 ⋅ d + 3 ⋅ 3 ⋅ d ⋅ d + d ⋅ 256 ) C \cdot (256\cdot d+3\cdot3\cdot d\cdot d+d\cdot 256) \tag 4 C⋅(256⋅d+3⋅3⋅d⋅d+d⋅256)(4)
的参数和等比例的FLOPs。当 C = 32 C=32 C=32并且 d = 4 d=4 d=4,方程4 ≈ 70 k \approx 70k ≈70k。表格2显示了 cardinality C C C 和瓶颈广度 d d d的关系。

表2. cardinality和广度的关系(以模板的conv2为例),粗略地维持了残差模块的复杂度。模板conv2的参数个数大约是70k。FLOPs大约是0.22b(# 参数x56x56)。
因为我们采用了3.1中提到的两个准则,那么上面提到的近似相等关系对于所有stage上的ResNet瓶颈模块和我们的ResNeXt都是成立的(除了特征图大小改变的降采样层)。表1比较了拥有相似容量的原始的ResNet-50和我们的ResNeXt-50。我们发现复杂度仅仅是大致相等,但是复杂度的不同是很小的,并不会影响我们的结果。
4. Implementation details
在ImageNet数据集上,输入图像是仿照GoogLeNet,先对图像进行大小和长宽比的resize的数据增广,然后再随机裁取224x224作为输入。捷径连接都是恒等映射除了需要变换维度的映射外。conv3,4,5的降采样都是在每个stage的第一个模块的3x3通过stride为2的卷积完成。我们使用minibatch为256的SGD在8个GPUs上训练(每个GPU上32)。使用0.9的momentum和0.0001的weight decay。我们初始lr为0.1,同样仿照GoogLeNet的策略,学习率减小三次,每次都是除以10。在所有的对照实验中,我们评估错误都是使用短边长为256的图片的中心224x224的crop来完成的。
我们的模型都是按照图3c的形式来实现的。BN是在卷积之后就执行的(也就是在跟捷径连接相加之前)。ReLU紧接着BN执行,除了连接捷径是在加了之后执行。
我们注意到只要BN和ReLU按照上面的方法来操作的话,那么图3的三种形式就是严格相等的。我们对三种形式都进行了训练得到了同样的结果。我们选择图3c,因为更加比其他两种方式更加简洁和更快。
5. Experiments
5.1. Experiments on ImageNet-1K
我们选择在ImageNet1000类分类任务上进行对比实验。仿照ResNet来构建50层和101层的残差网络,仅仅是将ResNet里的模块替换成我们的就行了。
Notations. 因为我们采用了3.1提到的两条规则,这就足够我们通过模板来构建网络。例如,表1展示了ResNeXt-50是通过一个cardinality为32和瓶颈width为4d的模板来搭建的(图3)。这个网络被记为ResNeXt-50(32 × \times ×4d)。我们注意到模板的输入输出的宽度都被固定为256维(图3),并且所有宽度维度每次特征图降采样都会翻倍(表1)。
Cardinality v s . vs. vs. Width. 我们首先按照表2在保存复杂度的情况下来评估 cardinality C 和瓶颈width。表3展示了结果,同时图5显示了错误率与epoch的关系。和ResNet-50相比,32x4d的ResNeXt-50的validation error为22.2%,比ResNet的基线23.9%要低了1.7%。随着cardinality C从1到32,在保持复杂度的情况下,error rate持续降低。32x4d的ResNeXt相比ResNet的拥有更低的training error。这意味着效果的提高并不是来自于泛化效果而是来自更好的特征表达。
同样的趋势也可以在ResNet-101中看到,32x4d的ResNeXt-101比对应的ResNet-101提高了0.8%。尽管validation error的提高比50层的要小,但是training error的提高仍然是很大的(ResNet-101的20%,ResNeXt-101的16%)。事实上,更多的训练数据会拉开validation error的差距,会在ImageNet-5K数据集上表现出来。
从表3,我们可以看出在保存复杂度的情况下,当瓶颈width很小的时候,以减少width的代价来增加cardinality得到的准确率增益已经饱和了。我们考虑到在这样的一个权衡中,继续降低width是不太值得的,所以我们就不继续采用比4d更小的瓶颈了。
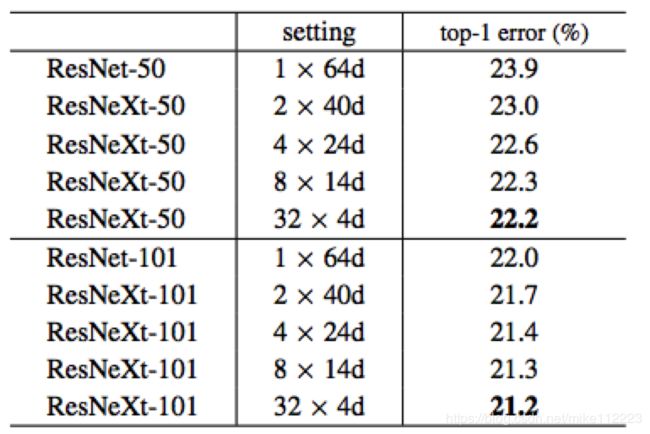
表3. 在ImageNet-1K上的对照实验。(上面)ResNet-50(保存了复杂度,~4.1B FLOPs);(下面)ResNet-101(保存复杂度,~7.8B FLOPs)。错误率都是在单一裁剪的224x224像素的图像上进行评估的。
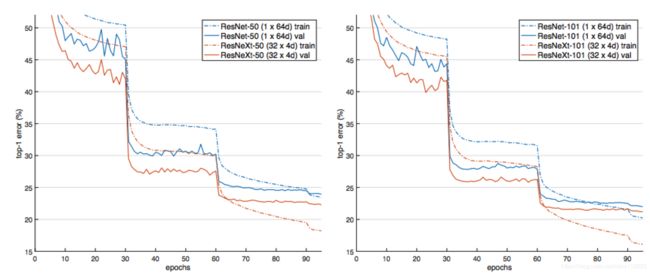
图5. ImageNet-1000上的训练error曲线。(左)ResNet/ResNeXt-50(保存复杂度,~4.1B FLOPs,25M参数);(右)ResNet/ResNeXt-101(保存复杂度,7.8B FLOPs,~44M参数)。
Increasing Cardinality v s . vs. vs. Deeper/Wider. 接下来我们探究通过增加C或者增加网络深度和宽度来增加复杂度。接下来的比较可以看做是ResNet-101基线的2倍FLOPs的网络。我们比较下面的变体(~15B的FLOPs)。i)Going deeper 到200层。ii)Going wider ,通过增加瓶颈width。iii)Increasing cardinality 翻倍cardinality。
从表4可以看出翻倍复杂度相比于ResNet-101基线(22.0%)是得到了更低的error。但是当网络深度更大或者更宽,取得的收益是小的(ResNet-200是0.3%,更宽的ResNet-101是0.7%)。
相比之下,增加cardinality C显示出了比增加深度和宽度更好的结果。 2x64d的ResNeXt-101(在1x64d ResNet-101的基线上翻倍C并且保持宽度)减小了1.3%的top1-error到20.7%。64x4d的ResNeXt-101(在32x4d ResNeXt-101的基线上翻倍C并且保持宽度)减小top1-error到20.4%。
我们也注意到32x4d ResNet-101(21.2%)比更深的ResNet-200和更宽的ResNet-101都表现得好,即使它只有将近后者~50%的复杂度。这再一次显示了C是相比于深度和宽度更有效的维度。
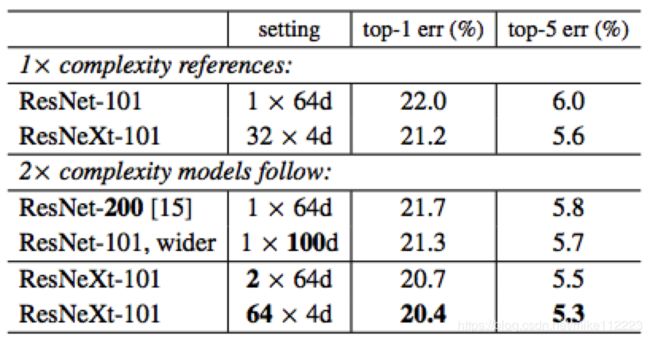
表4. 在ImageNet-1K数据集上,对ResNet-101和其两倍FLOPs的网络进行比较。错误率在单一裁剪的224x224像素的图像上进行评估。该实验要强调的是增加复杂度。
Residual connections. 接下来的表格显示了残差连接的效果:
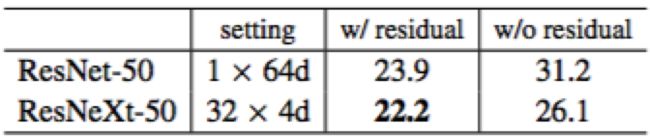
从ResNeXt-50上移除残差连接会增加error rate 3.9个点到26.1%。从ResNet-50的对应网络上移除残差连接会更差(31.2%)。这个比较显示了残差连接对于优化来说是有帮助的,并且聚合变换是有很强的表达能力的。
关于ImageNet-5K,CIFAR,COCO上的实验就不再赘述了。