自组织神经网络:自组织特征映射SOM网络
自组织神经网络
1、简介
SOM(Self-organizing feature Map)是一类“无监督学习”模型,一般的用法是将高维的input数据在低维的空间表示,因此SOM天然是一种降维方法。除了降维,SOM还可以用于数据可视化,以及聚类等应用中。
在生物神经系统中,存在着一种侧抑制现象,即一个神经细胞兴奋以后,会对周围其他神经细胞产生抑制作用。这种抑制作用会使神经细胞之间出现竞争,其结果是某些获胜,而另一些则失败。表现形式是获胜神经细胞兴奋,失败神经细胞抑制。自组织(竞争型)神经网络就是模拟上述生物神经系统功能的人工神经网络。
2、原理
SOM一共只有两层,即输入层和输出层(竞争层),在输出层中,同层的神经网络之间建立侧向连接,并可以通过权值的学习形成特定的模式。如一维线阵,二维平面和三维栅格阵等。具体节点排列为哪种模式,还需要根据之际需要去判断,比如,对于旅行路径类的问题,二维平面比较直观;对于一般的分类问题,一个输出节点即能代表一个模式类,用一维线阵就比较好。
竞争学习的步骤为:
(1)向量归一化
(2)寻找获胜神经元
(3)网络输出与权值调整
步骤(3)完成后回到步骤1继续训练,直到学习率衰减到0。学习率处于(0,1],一般随着学习的进展而减小,即调整的程度越来越小,神经元(权重)趋于聚类中心。
向量归一化
在竞争层中,如何寻找获胜神经元呢?对于输入的向量,将其与竞争层中的神经元对应的权重向量进行相似性比较,最相似的就是获胜神经元。ok,现在问题转化为了如何进行相似性比较,计算相似度的方法可以参考《距离计算方法总结》,以及《机器学习距离公式总结》,比较常见的计算距离的方法就是欧式距离和余弦相似度,此处不做过多介绍。向量归一化的意义在于:当两个向量都是模为1的单位向量时,欧式距离等价于余弦相似度(距离最小,相似度最大),而余弦相似度退化为向量内积。
权值初始化
在SOM中,有一个问题,就是竞争层中可能有些节点的权重一直不会更新,因为没有输入数据与他们距离相近,即出现了死结点,此时,为了避免出现死结点,竞争层权重的初始化就显得尤为重要,一般有以下两种方法:
- 一种简单易行的方法是从训练集中随机抽取m个输入样本作为初始权值
- 另一种可行的办法是先计算出全体样本的中心向量,在该中心向量基础上迭加小随机数作为权向量初始值,也可将权向量的初始位置确定在样本群中(找离中心近的点)。
权值调整域(优胜领域)
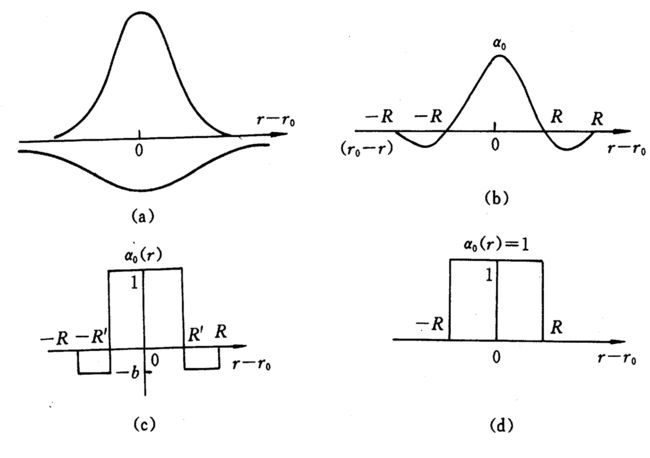
SOM网的获胜神经元对其邻近神经元的影响是由近及远,由兴奋逐渐转变为抑制,因此其学习算法中不仅获胜神经元本身要调整权向量,它周围的神经元在其影响下也要程度不同地调整权向量。这种调整可用三种函数表示,下图的bcd:
Kohonen算法:基本思想是获胜神经元对其邻近神经元的影响是由近及远,对附近神经元产生兴奋影响逐渐变为抑制。在SOM中,不仅获胜神经元要训练调整权值,它周围的神经元也要不同程度调整权向量。常见的调整方式有如下几种[2]:
- 墨西哥草帽函数:获胜节点有最大的权值调整量,临近的节点有稍小的调整量,离获胜节点距离越大,权值调整量越小,直到某一距离0d时,权值调整量为零;当距离再远一些时,权值调整量稍负,更远又回到零。如(b)所示
- 大礼帽函数:它是墨西哥草帽函数的一种简化,如(c)所示。
- 厨师帽函数:它是大礼帽函数的一种简化,如(d)所示。
以获胜神经元为中心设定一个邻域半径R,该半径圈定的范围称为优胜邻域。在SOM网学习算法中,优
胜邻域内的所有神经元均按其离开获胜神经元的距离远近不同程度地调整权值。 优胜邻域开始定得很大,但其大小随着训练次数的增加不断收缩,最终收缩到半径为零。
优胜领域设计原则是使领域不断缩小,这样输出平面上相邻神经元对应的权向量之间既有区别又有相当的相似性,从而保证当获胜节点对某一类模式产生最大响应时,其领域节点也能产生较大响应。领域的形状可以是正方形、六边形或者菱形。优势领域的大小用领域的半径表示,r(t)r(t)的设计目前没有一般化的数学方法,通常凭借经验来选择。下面是两种典型形式:
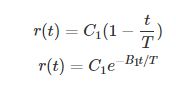
C1为于输出层节点数有关的正常数, B1为大于1的常数,T为预先选定的最大训练次数。
学习率的设计
学习率会影响收敛速度,可以定义一个动态的学习函数,随着迭代次数的增加而收敛。
Learn_rate(i)=maxLrate-((i+1.0)*(maxLrate-minLrate))/MaxIteration
其中,maxLrate为最大学习率,minLrate为最小学习率,MaxIteration为最大迭代次数,i为当前迭代次数。
SOM Kohonen 学习算法
算法总结如下:
Kohonen学习算法
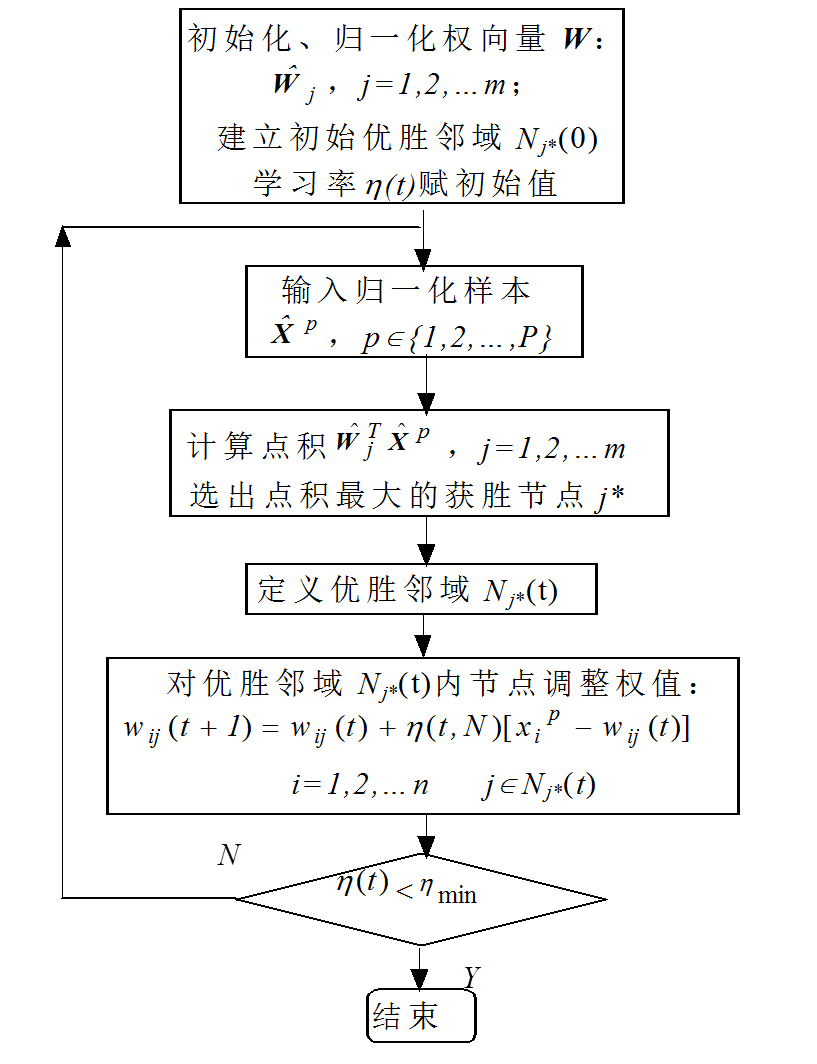
- 初始化,对竞争层(也是输出层)各神经元权重赋小随机数初值,并进行归一化处理,得到w^j,j=1,2,...mw^j,j=1,2,...m;建立初始优胜领域Nj∗(0)Nj∗(0);学习率ηη初始化;
- 对输入数据进行归一化处理,得到X^p,j=1,2,...PX^p,j=1,2,...P,总共有P个数据;
- 寻找获胜神经元:从X^pX^p与所有w^jw^j的内积中找到最大j∗j∗;
- 定义优胜邻域Nj∗(t)Nj∗(t)以j∗j∗为中心确定tt时刻的权值调整域,一般初始邻域Nj∗(0)Nj∗(0)较大,训练时Nj∗(t)Nj∗(t)随训练时间逐渐收缩;
-
调整权重,对优胜邻域Nj∗(t)Nj∗(t)内的所有神经元调整权重:
wij(t+1)=wij(t)+η(t,N)[xPi−wij(t)]i=1,2,...,nj∈Nj∗(t)wij(t+1)=wij(t)+η(t,N)[xiP−wij(t)]i=1,2,...,nj∈Nj∗(t)
其中ii是一个神经元所有输入边的序标。式中,η(t,N)η(t,N)是训练时间tt和邻域内第j个神经元与获胜神经元j∗j∗之间的拓扑距离N的函数,该函数一般有如下规律: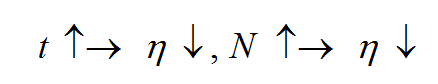
-
结束检查,查看学习率是否减小到0,或者以小于阈值。
算法流程图如下:
参考资料
1、机器学习之自组织特征映射神经网络(SOM)python实现(使用python具体实现SOM功能)
https://blog.csdn.net/qq_26645205/article/details/78285131
2、自组织神经网络介绍:自组织特征映射SOM(Self-organizing feature Map) (一篇很好的文章,很全面)
https://blog.csdn.net/xbinworld/article/details/50818803
3、机器学习之自组织特征映射神经网络(SOM)
https://blog.csdn.net/qq_26645205/article/details/78260079
4、利用ANN作图——自组织特征映射网络(SOFM)探究及实现
https://blog.csdn.net/diamonjoy_zone/article/details/65444840