PyTorch神经网络优化方法
PyTorch神经网络优化方法
- 了解不同优化器
- 书写优化器代码
- Momentum
- 二维优化,随机梯度下降法进行优化实现
- Ada自适应梯度调节法
- RMSProp
- Adam
- PyTorch种优化器选择
介绍几种优化器
参考链接:优化器比较
梯度下降法是最基本的一类优化器,目前主要分为三种梯度下降法:标准梯度下降法(GD, Gradient Descent),随机梯度下降法(SGD, Stochastic Gradient Descent)及批量梯度下降法(BGD, Batch Gradient Descent)。
SDG
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
Momentum
使用动量(Momentum)的随机梯度下降法(SGD),主要思想是引入一个积攒历史梯度信息动量来加速SGD。
从训练集中取一个大小为nn的小批量{X(1),X(2),…,X(n)}{X(1),X(2),…,X(n)}样本,对应的真实值分别为Y(i)Y(i),则Momentum优化表达式为:

动量主要解决SGD的两个问题:一是随机梯度的方法(引入的噪声);二是Hessian矩阵病态问题(可以理解为SGD在收敛过程中和正确梯度相比来回摆动比较大的问题)。
理解策略为:由于当前权值的改变会受到上一次权值改变的影响,类似于小球向下滚动的时候带上了惯性。这样可以加快小球向下滚动的速度。
Adam
Adam中动量直接并入了梯度一阶矩(指数加权)的估计。其次,相比于缺少修正因子导致二阶矩估计可能在训练初期具有很高偏置的RMSProp,Adam包括偏置修正,修正从原点初始化的一阶矩(动量项)和(非中心的)二阶矩估计。
torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
# SGD 就是随机梯度下降
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
# momentum 动量加速,在SGD函数里指定momentum的值即可
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
# RMSprop 指定参数alpha
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
# Adam 参数betas=(0.9, 0.99)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
PyTorch种优化器选择
在PyTorch深度学习框架中,实现的优化器覆盖了Adadelta、Adagrad、Adam、Adamax、RMSprop、Rprop等等。
为了直观地比较各个优化器的性能,我借助PyTorch框架用一个神经网络来解决一个二次函数的拟合问题。
import torch
from torch.autograd import Variable
import torch.nn.functional as F
import matplotlib.pyplot as plt
import torch.utils.data as Data
# super param
LR = 0.01
BATCH_SIZE=32
EPOCH=12
x = torch.unsqueeze(torch.linspace(-1,1,1000),dim = 1) #压缩为2维,因为torch 中 只会处理二维的数据
y = x.pow(2) + 0.2 * torch.rand(x.size())
print(x.numpy(),y.numpy())
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
dataset = torch_dataset,
batch_size = BATCH_SIZE,
shuffle = True,# true表示数据每次epoch是是打乱顺序抽样的
num_workers = 2, # 每次训练有两个线程进行的????? 改成 1 和 2 暂时没看出区别
)
class Net(torch.nn.Module): # 继承 torch 的 Module
def __init__(self):
super(Net, self).__init__() # 继承 __init__ 功能
# 定义每层用什么样的形式
self.hidden = torch.nn.Linear(1,20) # 隐藏层线性输出
self.predict = torch.nn.Linear(20,1) # 输出层线性输出
def forward(self, x): # 这同时也是 Module 中的 forward 功能
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net_SGD = Net()
net_Momentum = Net()
net_RMSProp = Net()
net_Adam= Net()
nets = [net_SGD,net_Momentum,net_RMSProp,net_Adam] # 一个比一个高级
opt_SGD = torch.optim.SGD(net_SGD.parameters(),lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(),lr = LR,momentum=0.8) # 是SGD的改进,加了动量效果
opt_RMSProp = torch.optim.RMSprop(net_RMSProp.parameters(),lr=LR,alpha=0.9)
opt_Adam= torch.optim.Adam(net_Adam.parameters(),lr=LR,betas=(0.9,0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSProp, opt_Adam]
# 比较这4个优化器会发现,并不一定越高级的效率越高,需要自己找适合自己数据的优化器
loss_func = torch.nn.MSELoss()
losses_his = [[],[],[],[]]
if __name__ == '__main__': # EPOCH + win10 需要if main函数才能正确运行,
for epoch in range(EPOCH):
print(epoch)
for step,(batch_x,batch_y) in enumerate(loader):
b_x = Variable(batch_x)
b_y = Variable(batch_y)
for net,opt,l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get_out for every net
loss = loss_func(output,b_y) # compute loss for every net
opt.zero_grad()
loss.backward()
opt.step() # apply gradient
l_his.append(loss.data[0]) # loss recoder
labels = ['SGD','Momentum','RMSProp','Adam']
for i,l_his in enumerate(losses_his):
plt.plot(l_his,label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim = ((0,0.2))
plt.show()
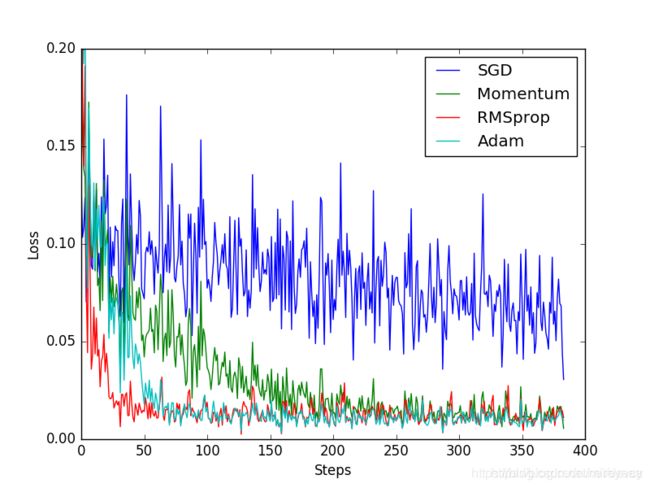
SGD 是最普通的优化器, 而 Momentum 是 SGD 的改良版, 它加入了动量原则. 后面的 RMSprop 又是 Momentum 的升级版. 而 Adam 又是 RMSprop 的升级版. 不过从这个结果中我们看到, Adam 的效果似乎比 RMSprop 要差一点. 所以说并不是越先进的优化器, 结果越佳. 我们在自己的试验中可以尝试不同的优化器, 找到那个最适合你数据/网络的优化器.
参考:
https://blog.csdn.net/devcy/article/details/89335575
https://ptorch.com/news/54.html