BD视觉算法工程师笔试题

选择题

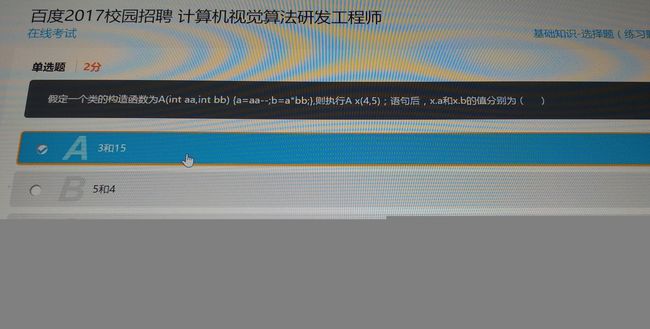
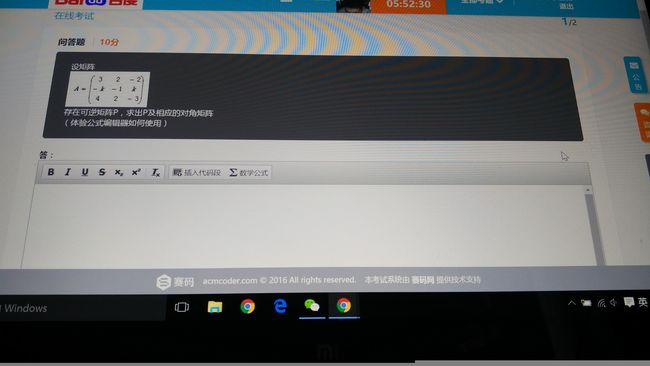
1

答案：D

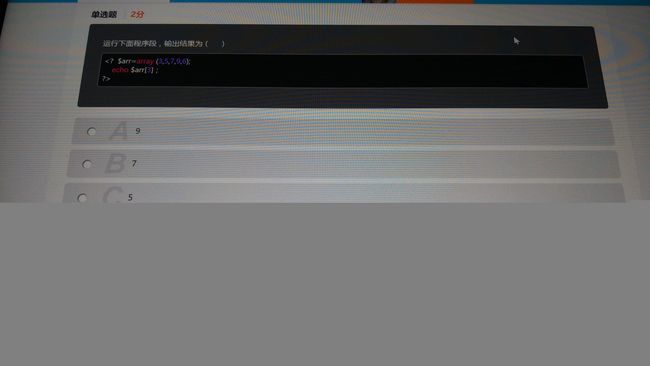
2

答案：A
此代码为PHP语言。

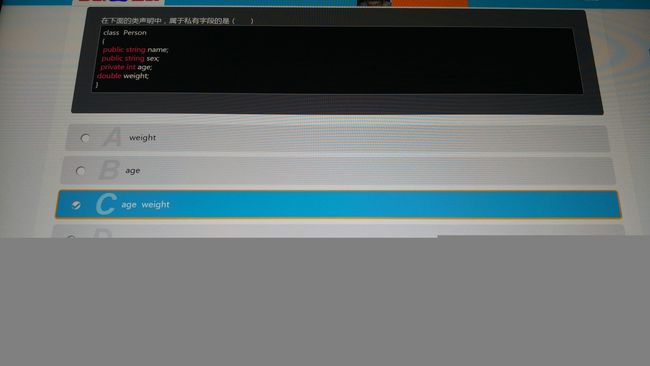
3

答案：A

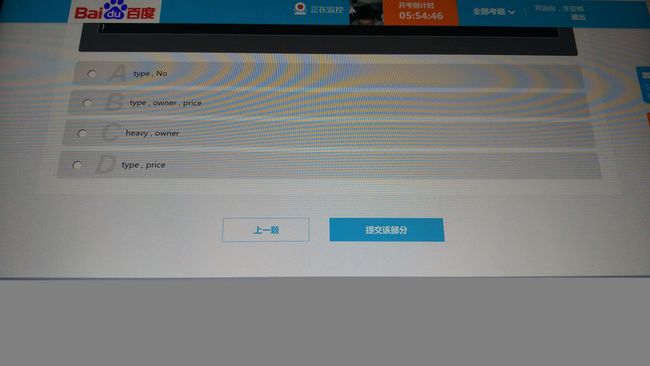
4

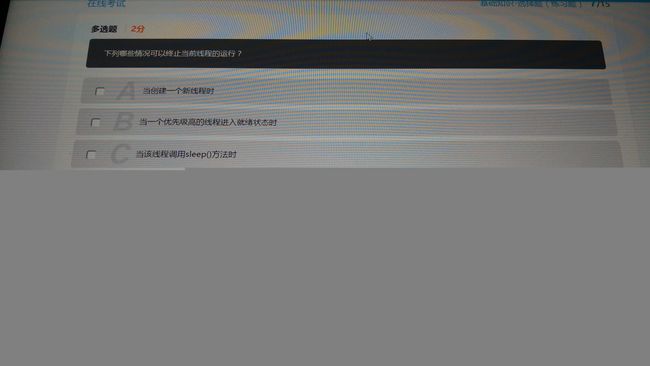
答案：D
当一个优先级高的线程进入就绪状态时，它只是有较高的概率能够抢到CPU的执行权，不是一定就能抢到执行权。
当前线程调用sleep()方法或者wait()方法时，只是暂时停止了该线程的运行，进入阻塞状态，不是终止线程。
当创建一个新的线程时，该线程也加入到了抢占cpu执行权的队伍中，但是是否能抢到，并不清楚。
线程结束的三个原因：
1、run方法执行完成，线程正常结束
2、线程抛出一个未捕获的Exception或者Error
3、直接调用该线程的Stop方法结束线程（不建议使用，容易导致死锁）
参考：下面那些情况可以终止当前线程的运行？

5

答案：CD
挂载设备使用mount，卸载设备使用umount，有三种方式，通过设备名，挂载点或者设备名和挂载点
如题目所示：
umount /dev/hdc
umount /mnt/cdrom
umount /mnt/cdrom /dev/hdc
参考：https://www.nowcoder.com/questionTerminal/85cc5714572341eba1bae15f86a98575?from=14pdf

6

答案：A
思索了很久有没有坑，原来没有

7

答案：D
find . -name “*.txt” 可以
find . -name “.txt”是找出文件名为.txt的文件
find . “.txt” 是查找”.”，”.txt”这两个目录

8

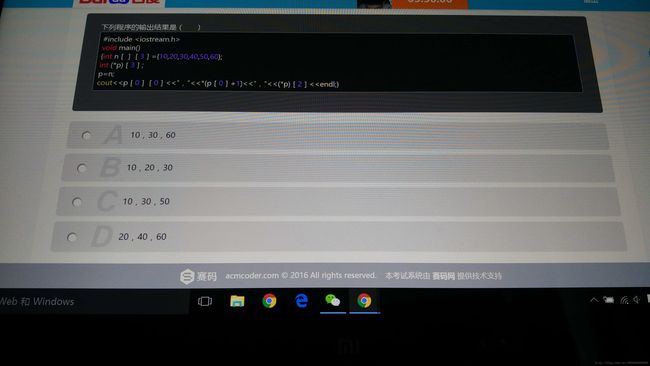
答案：B
指针数组：一个数组里装满了指针。int *a[10];
数组指针：一个指向数组的指针。 int (*a)[10]; 二维数组的数组名也是一个数组指针。
*a等价于a[0]，相当于让a下降了一级；&a表示“指向二维数组”的指针，相当于上升了一级。

9

答案：C
C#，此题不太确定啊

10

答案：C

11

答案：D

填空题

13

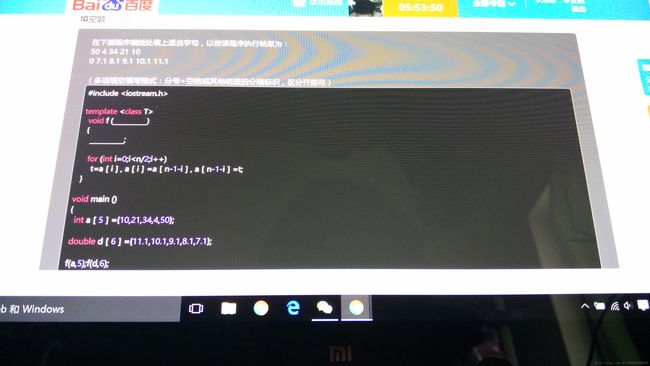
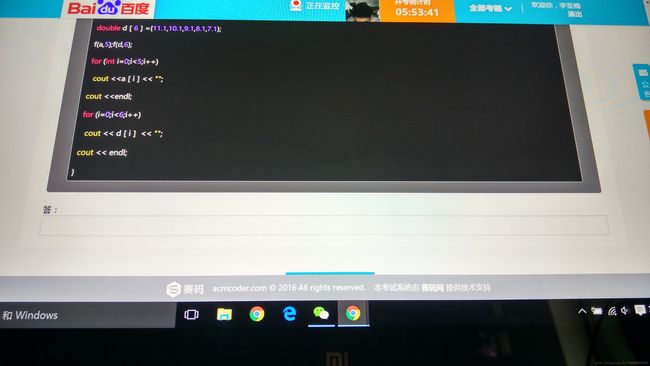
答案：(1)T a[], int n
(2)T t;
函数模板

15

答案：(1)cin >> a >> b >> c;
(2)s=pow(l*(l-a)*(l-b)*(l-c), 0.5);
考察三角形面积计算公式。

16

答案：(1)static int x;
(2)int Test::x=33;
考察类的静态成员变量。

问答题

17

18

享受咖啡，缓解压力。咖啡深受上班一族的青睐，是上班人士调节生活、聚会、缓解工作压力等的首选饮品。咖啡自动售卖机或咖啡室更是大型公司不可或缺的服务，所以此次app的应用场景定位为大型公司的服务区内。
目标人群：
大型公司里的各阶层员工
使用场景：
a)多种样式可综合比较选购或推荐；
b)单人或多人如聚会、商讨项目等时预约选购；
c)定时设置如提前提醒拿取咖啡；
d)通过评价分享心得促进交流等。
设计要点：
a.多种花式咖啡查看选择；
b.借鉴淘宝等常用购买平台设计方式符合人们的常规思维习惯
c.app应用与自售机交互方式采用常见的二维码形式；
d.用户可根据需要预定咖啡以及分享推荐等。
参考：http://yazizzy.lofter.com/post/13431a_2975457

考前测试

19

#include
#include
#include
using namespace std;

int main() {
    float a;
    int n;
    while (cin >> a >> n) {
        float sum = a;
        for (int i = 1; isqrt(a);
            sum += a;
        }
        printf("%.2f\n", sum);
    }
    return 0;
}

21

#include
#include
using namespace std;

int main() {
    int m, n;
    while (cin >> m >> n) {
        vector<int> v;
        for (int i = m; i <= n; i++) {
            if (i == pow(i / 100, 3) + pow(i % 100 / 10, 3) + pow(i % 10, 3)) {
                v.push_back(i);
            }
        }
        if (v.empty()) cout << "no" << endl;
        else {
            for (int i = 0; icout << v.at(i) << " ";
            cout << endl;
        }
    }
    return 0;
}

问答题

23

静态链接：指程序编译时直接把静态库（Static Linked Library，’.lib’）中调用的函数代码链接进目标程序，因此程序运行时不再需要它的库文件。
动态链接：指把调用函数所在的动态库（Dynamic Linked Library，’.dll’）和调用函数在文件中的位置等信息链接进目标程序，程序运行时再从DLL中寻找相应函数代码，因此需要相应DLL文件的支持。
区别：动态库是运行时才加载到内存中，程序运行时可以随意加载或移除；静态库是编译时就加载到内存中，不能手动移除。
参考：静态链接与动态链接的区别

24

冒泡排序（ O(n2) ），快速排序（ O(nlog2n) ）,堆排序（ O(nlog2n) ），归并排序（ O(nlog2n) ）,基数排序（ O(n+k) ）

25.

SIFT(Scale Invariant Feature Transform)特征对旋转、尺度缩放、亮度变化等保持不变性，是非常稳定的局部特征。
SIFT的主要思路：a)构造图像的尺度空间表示，b)在尺度空间中搜索图像的极值点，c)由极值点建立特征描述向量，d)用特征描述向量进行相似度匹配。
检测：通过图像与DOG算子卷积得到一幅二维图像在不同尺度下的尺度空间表示（即DOG图像）；然后通过每个像素点与其三维领域的临近点进行比较，找出DOG局部极值点作为初步的特征点；然后通过曲线拟合（临近信息插补）得到特征点的精确位置，同时也会舍弃那些不明显关键点和边缘响应；接下来利用特征点邻域像素的梯度分布来确定特征点的方向。每个特征点都包含三个信息 (x,y,σ,θ) ，即位置、尺度和方向。
描述：描述子将被用来作为目标匹配的依据，所以应具有较高的独特性以保证匹配率。特征描述大致包含三个步骤：1.旋转主方向，即将坐标轴旋转为关键点方向，以确保旋转不变性。2.然后在特征点对应的高斯图像上统计其 16∗16 邻域内的方向梯度，将统计向量作为该点的sift描述子。3.特征向量的常规归一化，进一步去除光照变化等影响。
匹配：RANSAC(RANdom SAmple Consensus)方法是当前常用的一种特征点对的匹配算法，在OpenCV中我们可以使用暴力匹配（BruteForceMatcher）和FLANN（Fast Library for Approximate Nearest Neighbors，快速最近邻逼近搜索函数库）实现快速高效匹配。另外由于噪声等其他因素影响，有时次优匹配点可能和最优匹配点非常接近（接近 0.8 ），实验证明舍弃这些点效果会更好。
参考：Introduction to SIFT (Scale-Invariant Feature Transform)；《数字图像处理MATLAB版（左飞著）》12.1章；《OpenCV3编程入门》第11章

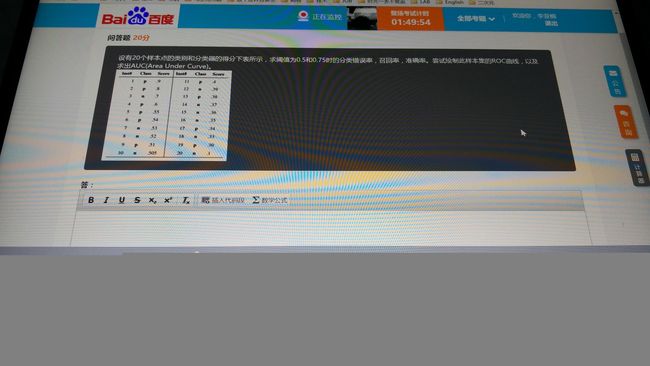
26

1.计算错误率、准确率和召回率

Inst#	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
class	P	P	N	P	P	P	N	N	P	N	P	N	P	N	N	N	P	N	P	N
Score	0.9	0.8	0.7	0.6	0.55	0.54	0.53	0.52	0.51	0.505	0.4	0.39	0.38	0.37	0.36	0.35	0.34	0.33	0.30	0.1
Result when 0.5	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN
Result when 0.75	TP	TP	TN	FN	FN	FN	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN

注：TP(真正例)，FP(假正例)，FN(假反例)，TN(真反例)

性能度量	错误率F	准确率P	召回率R
公式	F=FP+FNTP+FP+TN+FN	P=TPTP+FP	R=TPTP+FN
Result when 0.5	4+420=0.4	610=0.6	66+4=0.6
Result when 0.75	0+820=0.4	22=1.0	22+8=0.2

2.绘制此样本的ROC曲线

Inst#	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	真正例率TPR	假正例率FPR
class	P	P	N	P	P	P	N	N	P	N	P	N	P	N	N	N	P	N	P	N	True Positive Rate	False Positive Rate
Score	0.9	0.8	0.7	0.6	0.55	0.54	0.53	0.52	0.51	0.505	0.4	0.39	0.38	0.37	0.36	0.35	0.34	0.33	0.30	0.1	TPR=TPTP+FN	FPR=FPFP+TN
Result when 1.0	FN	FN	TN	FN	FN	FN	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	00+10=0	00+10=0
Result when 0.9	TP	FN	TN	FN	FN	FN	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	11+9=0.1	00+10=0
Result when 0.8	TP	TP	TN	FN	FN	FN	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	22+8=0.2	00+10=0
Result when 0.7	TP	TP	FP	FN	FN	FN	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.2	11+9=0.1
Result when 0.6	TP	TP	FP	TP	FN	FN	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	\0.3	0.1
Result when 0.55	TP	TP	FP	TP	TP	FN	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.4	0.1
Result when 0.54	TP	TP	FP	TP	TP	TP	TN	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.5	0.1
Result when 0.53	TP	TP	FP	TP	TP	TP	FP	TN	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.5	0.2
Result when 0.52	TP	TP	FP	TP	TP	TP	FP	FP	FN	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.5	0.3
Result when 0.51	TP	TP	FP	TP	TP	TP	FP	FP	TP	TN	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.6	0.3
Result when 0.505	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	FN	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.6	0.4
Result when 0.4	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	TN	FN	TN	TN	TN	FN	TN	FN	TN	0.7	0.4
Result when 0.39	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	FN	TN	TN	TN	FN	TN	FN	TN	0.7	0.5
Result when 0.38	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	TN	TN	TN	FN	TN	FN	TN	0.8	0.5
Result when 0.37	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	FP	TN	TN	FN	TN	FN	TN	0.8	0.6
Result when 0.36	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	FP	FP	TN	FN	TN	FN	TN	0.8	0.7
Result when 0.35	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	FP	FP	FP	FN	TN	FN	TN	0.8	0.8
Result when 0.34	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	FP	FP	FP	TP	TN	FN	TN	0.9	0.8
Result when 0.33	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	FP	FP	FP	TP	FP	FN	TN	0.9	0.9
Result when 0.30	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	FP	FP	FP	TP	FP	TP	TN	1.0	0.9
Result when 0.1	TP	TP	FP	TP	TP	TP	FP	FP	TP	FP	TP	FP	TP	FP	FP	FP	TP	FP	TP	FP	1.0	1.0

现实任务中通常是利用有限个测试样例来绘制ROC图，绘图过程很简单：给定 m+ 个正例和 m− 个反例，根据学习器预测结构对样例进行排序，然后把分类阈值设为最大，即把所有样例均预测为反例，此时真正例率和假正例率均为0，在坐标 (0,0) 处标记一个点。然后，将分类阈值依次设为每个样例的预测值，即依次将每个样例划为正例。设前一个标记点坐标为 (x,y) ，当前若为真正例，则对应标记点的坐标为 (x,y+1m+) ；当前若为假正例，则对应标记点的坐标为 (x+1m−,y) ，然后用线段连接相邻点即得。
画出其ROC曲线图：

可得到其 AUC=0.68
画图python代码：

import matplotlib.pyplot as plt

x = [0.0, 0.0, 0.0, 0.1, 0.1, 0.1, 0.1, 0.2, 0.3, 0.3, 0.4, 0.4, 0.5, 0.5, 0.6, 0.7, 0.8, 0.8, 0.9, 0.9, 1.0]
y = [0.0, 0.1, 0.2, 0.2, 0.3, 0.4, 0.5, 0.5, 0.5, 0.6, 0.6, 0.7, 0.7, 0.8, 0.8, 0.8, 0.8, 0.9, 0.9, 1.0, 1.0]
plt.plot(x, y, 'ro')
plt.plot(x, y)
plt.axis([0, 1, 0, 1])
plt.title(r'ROC')
# shorthand is also supported and curly's are optional
plt.xlabel(r"False positive rate", fontsize=10)
plt.ylabel(r"True positive rate", fontsize=10)
plt.show()

27

#include
#include
using namespace std;

void test(vector<int> v, int k);
int main() {
    vector<int> v1 = { 3, 4, 5, 6, 7, 8 };
    vector<int> v2 = { 3 };
    vector<int> v3 = {};
    test(v1, 3);  //常规测试
    test(v1, 5);
    test(v1, 8);
    test(v2, 3);  //边界测试
    test(v1, 0);  //负面测试
    test(v3, 3);
    return 0;
}
int deleteK(vector<int> &v, int k);
void test(vector<int> v, int k) {
    int len = deleteK(v, k);
    cout << "The array after delete k is: ";
    for(int i = 0; icout << v.at(i) << " ";
    }
    cout << endl;
}
int deleteK(vector<int> &v, int k) {
    int sizeOfV = v.size();
    int index = 0;
    for (int i = 0; iif (v.at(i) != k) {
            v.at(index) = v.at(i);
            index++;
        }
    }
    return index;
}

29

1）线性SVM的原始问题：

minw,b,ξ12∥w∥2+C∑i=1Nξis.t.yi(w∗xi+b))≥1−ξi,i=1,2,...,Nξi≥0,i=1,2,...,N

其对偶问题是：

minα12∑i=1N∑j=1Nαiαjyiyj(xi∗xj)−∑i=1Nαis.t.∑i=1Nαiyi=00≤αi≤C,i=1,2,...,N

2）

原始问题属于凸二次规划问题，具有全局最优解，有许多最优化算法可以应用于这一问题的求解。可应用拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解。当训练样本容量很大时，可使用序列最小最优化（sequential minimal optimization, SMO）算法。

3）

SVM处理多分类问题

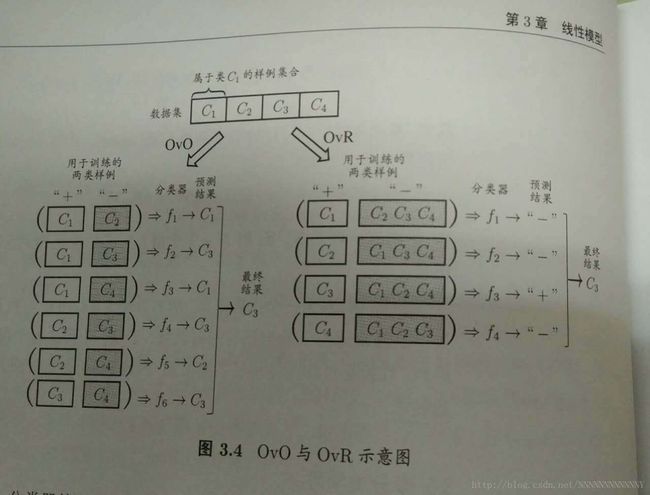
SVM是一个二分类器，处理多分类问题时，常用的策略有：“一对一”（One vs. One, 简称OvO）、“一对其余”（One vs. Rest, 简称OvR）和“多对多”（Many vs. Many，简称MvM）。
OvO：对于给定数据集 D=(xi,yi),(x2,y2),...,(xm,ym),yi∈C1,C2,...,CN 。OvO将这N个类别两两配对，从而产生 N(N−1)/2 个二分类任务。测试阶段，新样本将同时提交给所有分类器，于是我们可得到 N(N−1)/2 个分类结果，最终把被预测得最多的类别作为最终分类结果。
OvR：每次将一个类的样例作为正例，所有其他类的样例作为反例来训练N个分类器。在预测时选择置信度最大的类别作为分类结果。
MvM：每次将若干个类作为正类，若干个其他类作为反类。

4）Linear SVM与LR的异同

• Linear SVM和LR都是线性分类器
• Linear SVM不直接依赖于数据分布，分类平面不受一类点影响；LR则受所有数据点的影响，如果数据不同类别strongly unbalance一般需要先对数据做balancing。
• Linear SVM依赖数据表达的距离测量，所以需要对数据先做normalization；LR不受其影响
• Linear SVM依赖penalty的系数，实验中需要做validation
• Linear SVM和LR的performance都会受到outlier的影响，其敏感程度而言，谁更好很难下明确结论。
  参考：Linear SVM 和 LR 有什么异同？
  5）SVM与神经网络的关系
• 线性SVM的计算部分和一个单层神经网路一样，都是一个矩阵乘积。SVM的关键在于它的Hinge Loss以及maximum margin的想法，其实这个loss也可以应用在神经网络里。
• 对于处理非线性任务时，SVM和神经网络走了两条不同的路：神经网络通过多个隐层+激活函数的方法来实现非线性的函数；SVM则采用了kernel trick的方法。两者各有好坏，神经网络的好处是网络设计可以很灵活；SVM的理论很漂亮，但是kernel设计不是那么容易。
  参考：SVM（支持向量机）属于神经网络范畴吗？

30

1）发展流程
a)滑窗式区域选择+SIFT、HOG等特征提取+SVM、Adaboost分类器
b)基于Region Proposal的深度学习目标检测算法，RPN(Region Proposal Networks)
c)基于回归方法的深度学习目标检测，YOLO,SSD
参见：
现在基于CNN的方法《基于深度学习的目标检测研究进展》
也可以了解下传统的比较老的方法《图像物体分类与检测算法综述》