8种常用的排序算法
8种常用的排序算法
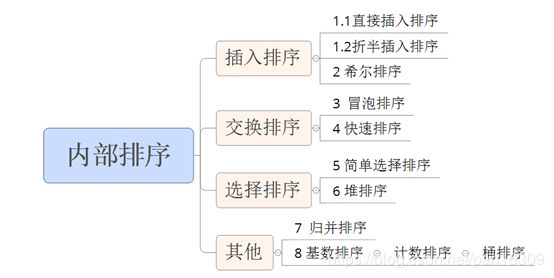
数据结构中的排序是非常重要的知识,将数据排序是处理数据的基本起手操作。从类型上分排序可以分为内部排序和外部排序,对保存在内存中的数据进行排序成为内部排序,对保存在磁盘上的数据排序称为外部排序。
本文将对内部排序常用的8中排序做一个简单介绍,作为一个程序员,需要熟练掌握这8种常用的排序,理解其排序思想,并能以代码实现。
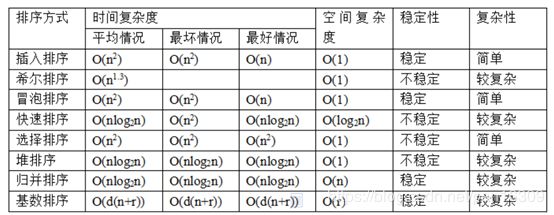
8种排序中的时间复杂度和空间复杂度一览
可以看到,所有排序中除了基数排序时间复杂度不确定之外,平均时间复杂度最好的是快排,堆排,归并;而快排需要空间复杂度o(log2n),归并需要的空间复杂度o(n),堆排需要空间复杂度为o(1),所以综合来说堆排是空间和时间合起来最理想的办法。但是堆排和快排都是不稳定的排序,所谓不稳定,就是相同的两个数据在排序前后相对位置可能会改变。当我们希望排序的结果是稳定的时,就需要牺牲一定空间选择使用归并排序。
当然数据量比较小时,可以直接采用复杂性比较低的插入和冒泡排序,其代码简单易懂,顺手就能写出来。
下面介绍各个排序的实现代码以及原理
交换数据的宏:
#define SWAP(a,b) {int temp = a;a=b;b=temp;}1.1 直接插入排序
void myInsertSort(int *arr, int len)
{
int i, j,temp;
for (i = 1; i < len; i++)
{
temp = arr[i];//从下一个元素找
for (j = i - 1; j>0 && arr[j] > temp; j--)//在已经排好序的0到i-1个元素中,找到待插入元素的位置,从后向前插入
{
arr[j + 1] = arr[j]; //把插入位置后的元素都向后挪
}
arr[j+1] = temp; //j后面就是要插入的位置
}
}直接插入排序是最简单也最直观的方法,和打扑克牌的时候理牌一样的道理,先选第一个元素作为有序元素(一个元素自然有序),再一一将后面的元素逐一与已经有序排列的元素比较,找到其插入的位置,静态数组中需要将后面所有的数据后移一个位置,链式数据则直接将新元素插入该位置。在链表的有序插入算法里,常用插入排序直接获得一个有序的链表。
1.2 折半插入排序
void myHalfInsertSort(int *arr, int len)
{
int i, j, temp,low,high,mid;
for (i = 1; i < len; i++)
{
temp = arr[i];//从下一个元素找
low = 0;
high = i - 1; //在已经排好序的序列中二分查找
while (low <= high)
{
mid = (low + high) / 2; //取中间的下标
if (arr[mid] > temp)high = mid - 1; //在左半部分
else low = mid + 1; //在右半子表
}
for (j = i - 1; j >= high + 1; j--)//在已经排好序的0到i-1个元素中,找到待插入元素的位置,从后向前插入
{
arr[j + 1] = arr[j]; //把插入位置后的元素都向后挪
}
arr[high + 1] = temp; //j后面就是要插入的位置
}
}折半插入与直接插入的区别就是在寻找插入位置时使用折半查找的方式查找,预期的查找次数是log2n,但是总体排序的次数并没有下降,所以时间复杂度是一样的。
2 希尔排序
希尔排序是牛逼的希尔大佬对直接插入排序算法做了改进的一种排序方法,首先取一个d1 3 冒泡排序 冒泡排序是开始学习C语言就会学习的一个排序算法,通过两层循环不断将符合的元素向上移动,类似冒泡因而得名,不多介绍,直接上代码 4 快速排序 快速排序是常用的几种排序中空间时间最优秀的排序,可以适用各种数据结构,在程序员面试的时候也会经常考到。快排的方法是先给定一个数,然后将待排序的数据分别于这个数比较,用两个标志记录i,k,i记录从左到右的遍历下标,k记录比给定的元素小的元素个数,比这个数大的放在右边,比这个数小的放在左边,k为当前这个数在数据表中的排序后位置,而后分别对左边和右边的数据做递归引用排序,最终就能得到有序的数据 这个算法的关键是要写对分割函数,但是由于它是递归的排序,当数据量很大时排序会占用很大的堆栈空间,因此这时候需要用非递归的算法实现。 非递归的快排 C语言中提供了快速排序的接口qsort,可以实现非递归的快速排序,在使用这个接口时,编写好对应的compare函数即可,其算法实现比较复杂很难记,可以不深入研究。函数参数列表: qsort(待处理数据入口地址,数据总个数,单个数据长度,compare函数) 对于需要排序的数据时结构体,需要根据其某个成员的值进行排序时,只需要重写相应的compare函数,将结构体成员比较的结果传入qsort接口即可 排序调用形式 5 简单选择排序 与插入排序不同,简单选择排序是对n个元素的数据遍历n次,每次选出一个最小的数据放到前面,第i次从第i到第n个数据中选出最小的数据放到位置i,从而得到有序数据 6 堆排序 堆排序是将待排序的数组在排序开始时建成大顶堆或者小顶堆,而后将堆顶元素与数组最后一个元素交换,将剩下的元素作为新的堆进行调整,反复这一过程直到所有堆中只剩一个元素。通过大顶堆的方式得到的数据序列是升序序列,而小顶堆则相反。堆本身是存在数组里的一颗完全二叉树,有关堆的概念和建堆的方法不多做叙述,可以参考王道7.4选择排序之堆排序的内容,或者百度之。堆排序的关键是堆调整的代码 大顶堆算法: 经过大顶推排序,得到的是升序序列 小顶堆算法: 经过小顶堆排序,得到的数据序列是降序序列 7 归并排序 归并排序的思想,是将有序序列分组进行排序,第一趟两两归并分成n/2(n为偶数)或者n/2+1(n为奇数)组,第二趟将分好组的数据再次两两归并排序,反复操作直到只剩下一个长度为n的有序数据表为止,每次归并的时候,小组内的成员是有序的。 不难看出,归并排序的算法和快速排序的算法一样可以使用递归的方式实现,先将两个元素排好序,然后归并。 这个算法是递归算法,因为递归是需要占用堆栈的,所以当数据量很大的时候就不能再用这个算法排序了。 接下来是归并排序的非递归算法,其思想是从长度为2的分组开始进行一趟排序,将分组长度加倍,重复执行一趟归并排序,直到长度为n 8 计数排序 计数排序的代码实现是最简单的,而在数据的变化范围不大的时候,计数排序的排序速度比快排堆排还要快,在统计学生分数,排名时常用这种排序,是一种空间换时间的排序。具体思想是开辟一个涵盖可能出现的所有值的数组,数组下标就是可能出现的值,遍历一遍待排序的数据,统计各个数据出现的次数,然后再按照下标,将排好序的数据存储到数组中,就可以得到有序数据 比较四个效率较高的排序算法排序100000000个1到1000的数的排序速度 快排45s,堆排43s,不相上下,没想到的是归并排序居然以22s的成绩遥遥领先,看来就算是相同数量级的时间复杂度,在真正执行时耗时也是有些区别的。 接下来出场的是黑马选手计数排序//希尔排序
void myShellSort(int *arr, int len)
{
int dk, i, j, temp;
for (dk = len >> 1; dk >= 1; dk = dk >> 1) //dk = n/2 ,di+1 = di/2 ,dn=1
{
for (i = dk; i < len; i++)
{
temp = arr[i];//从下一个元素找
for (j = i - dk; j>=0 && arr[j] > temp; j-=dk)//在组内进行插入排序,从后往前找
{
arr[j + dk] = arr[j]; //把插入位置后的元素都向后挪
}
arr[j + dk] = temp; //j后面就是要插入的位置
}
}
}//冒泡排序
void myBubbleSort(int *arr,int len)
{
int i, j;
int temp;
for (i = 0; i < len; i++)
{
for (j = i; j < len; j++)
{
if (arr[i]>arr[j])
{
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
}
}
//快速排序 递归形式实现
int partition(int *arr, int left, int right)
{
//传入数组与左右分割点的下标
int i, j;
for (i = j = left; i < right; i++)
{
if (arr[i] < arr[right]) //默认的起始分割点为最右元素
{
SWAP(arr[i], arr[j]);
j++;
}
}
SWAP(arr[j], arr[right]);
return j;
}
void myQucikSort(int *arr, int left,int right)
{
int pivot;
if (leftint compare(const void * a, const void * b)
{
int *pp1 = (int*)a;
int *pp2 = (int*)b;
if (*pp1 > *pp2)
{
return 1;
}
else if (*pp1 < *pp2)
{
return -1;
}
else return 0;
}typedef struct {
int mem1;
char mem2[10];
}stu_str,*pstu;
//根据成员的值比较大小返回比较结果
int compare_mem1(const void *left, const void *right)
{
pstu *pp1 = (pstu *)left;
pstu *pp2 = (pstu *)right;
if ((*pp1)->mem1 > (*pp2)->mem)
return 1;
else if ((*pp1)->mem1 < (*pp2)->mem1)return -1;
else return 0;
}qsort(stug, 5, sizeof(pstu), compare_mem1);//选择排序
void mySelectSort(int *arr, int len)
{
int i, j,min;
for (i = 0; i < len - 1; i++)
{
min = i;
for (j = i + 1; j < len; j++)
{
if (arr[min] > arr[j])
{
min = j;
}
}
if (min != i)SWAP(arr[i], arr[min]);
}
}//堆排序
//将子树调整为大根堆
//传入参数:根节点位置,堆元素个数,每次调整一个元素
void adjustMaxHeap(int *arr,int adjustPoint,int len)
{
int son = adjustPoint * 2 + 1; //传入的是数组下标,需要+1修正,son是左子树的下标
int dad = adjustPoint; //父节点下标
while (son < len)
{
if (son + 1 < len && arr[son] < arr[son+1]) //找到子节点中最大的节点
{
son++;
}
if (arr[son] > arr[dad]) //如果子节点大于父节点,交换父子节点
{
SWAP(arr[son], arr[dad]);
dad = son; //以当前节点为父节点向下调整
son = 2 * dad + 1; //获得下次检查的子节点下标
}
else{
break;
}
}
}
void myMaxHeapSort(int *arr,int len)
{
//step1 建立初始大根堆
int i;
for (i = len /2 - 1; i >= 0; i--) //从最后一个叶子节点的父亲节点开始调整
{
adjustMaxHeap(arr, i, len);
}
//step2 将堆顶元素逐一调整到列表最后(输出)
SWAP(arr[0], arr[len - 1]);
for (i = len - 1; i > 0; i--)
{
adjustMaxHeap(arr, 0, i); //将堆顶元素输出后对剩下的元素做大顶堆调整
SWAP(arr[0], arr[i - 1]);
}
}//将数据调整为小顶堆
void adjustMinHeap(int *arr,int adjpoint,int len)
{
int dad = adjpoint;
int son = dad * 2 + 1;
while (son < len)
{
if (son + 1 < len && arr[son] > arr[son + 1]) //获得较小的子节点
{
son++;
}
if (arr[son] < arr[dad])
{
SWAP(arr[son], arr[dad]);
dad = son;
son = dad * 2 + 1;
}
else
break;
}
}
//小顶堆排序
void myMinHeapSort(int *arr, int len)
{
int i;
//step 1 初始建立小顶堆
for (i = len / 2 - 1; i >= 0; i--)
{
adjustMinHeap(arr, i, len);
}
//step2 将小顶堆输出
SWAP(arr[len - 1], arr[0]);
for (i = len - 1; i > 0; i--)
{
adjustMinHeap(arr,0,i);
SWAP(arr[i-1],arr[0]);
}
}//归并排序
//归并排序需要一个空间为n的辅助数组,需要提前将辅助数组准备好并传入其地址
void Merge(int *arr, int *buff, int low, int mid, int high)
{
//*arr中low到min,min+1到high元素分别有序,将他们合并成一个有序表
int i, j, k;
//合并两个有序表的算法很简单,使用一个辅助数组将数据保存,再从中挑出较小的数据存回原数组
//当一个表数据取完时,将另一个表连接到原数组后面即可
for (k = low; k <= high; k++)
{
buff[k] = arr[k];
}
for (i = k = low, j = mid + 1; i <= mid && j <= high; k++)
{
if (buff[i] <= buff[j])
{
arr[k] = buff[i];
i++;
}
else
{
arr[k] = buff[j];
j++;
}
}
while (i <= mid)
{
arr[k] = buff[i];
k++;
i++;
}
while (j <= high)
{
arr[k] = buff[j];
k++;
j++;
}
}
//注意传入的参数high是数组下标
void myMergeSort(int *arr,int *buff,int low,int high)
{
int mid = (low + high) / 2;
if (low < high) //递归退出条件,归并组中元素只有两个时退出
{
myMergeSort(arr, buff, low, mid);
myMergeSort(arr, buff, mid+1, high);
Merge(arr, buff, low, mid,high);
}
}//进行一趟归并,gap是归并的长度除以2
void mergeOneRount(int *arr, int *buff, int len, int gap)
{
int i = 0;
//对每个组进行重复归并排序
while (i <= len - 2 * gap + 1)
{
Merge(arr, buff, i, i + gap - 1, i + 2 * gap - 1);
i = i + 2 * gap;
}
//因为最后一个组的长度可能不等于2*gap,需要单独处理
if (i + len - 1//计数排序
void myCountSort(int *arr, int len, int range)
{
int *count = (int*)calloc(range, sizeof(int));
int i,j;
//统计每个值的数据出现的次数
for (i = 0; i < len; i++)
{
count[arr[i]]++;
}
//按照值和次数将数据重新写入输出的数组中
for (i = 0; i < range; i++)
{
for (j = 0; j < count[i]; j++)
{
*arr = i;
arr++;
}
}
}