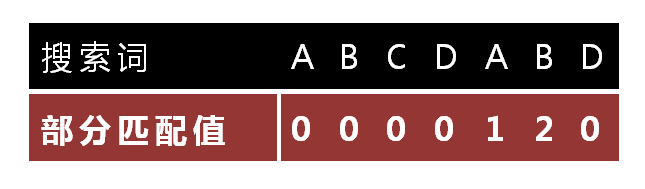在看算法基础书籍时,看到KMP算法的解释是用的DFA(有限状态自动机),看的我一脸懵逼。所以,就去网上搜索有没有更容易理解的方式去实现KMP算法。
看了很多篇,感觉下面这篇博文讲的比较清楚,但是也花了我挺长时间去看懂的。(好吧好吧,智商不足=_=)
KMP,深入讲解next数组的求解
后面经过自己的思考总结,在这里记录一下自己对KMP算法的理解和实现。
KMP算法的原理
关于KMP算法的原理,上面给出的链接里写的很详细了,这里简要的说一下。
假如在字符串 "ABCDABEFABCDABDE" 要查找 "ABCDABD" 的话,当我们遍历匹配到最后一个字符D的时候:
ABCDAB E FABCDABDE
ABCDAB D
发现不匹配的时候,按照最容易想到的暴力算法,应该是往后移一位,再重新从头开始进行比较:
A B C D A B E F ABCDABDE
A B C D A B D
显然,这些一位一位的往后移的比较是没有意义的,我们通过观察就能知道,应该直接往后移4位,让子字符串里的开头两个字符 AB 对齐原字符串,再从第三个字符 C 开始比较:
A B C D A B E F A B C DEABDE
A B C D A B D
所以重点是如何利用子字符串自己本身自带的这些信息来帮助我们跳过一些不必要的比较。下面来分析一下 "ABCDABD" 这个字符串的特点。
假如我们在原字符串查找
"ABCDABD"的第1个字符A就发现不匹配,那不用说,直接往后移1位。假如匹配到了
"ABCDABD"的第2个字符AB发现不匹配,那还是直接往后移1位。假如匹配到了 第3,4,5个字符
ABCDA发现不匹配,也没有可利用的条件,那还是直接往后移1位。当我们匹配到了
"ABCDABD"的第6个字符"ABCDAB"的时候,发现不匹配,但是,前5个字符"ABCDA"是已经匹配成功了的,并且结尾的字符A与开头的字符A重复了.显然我们可以移动4位,让开头的字符A与结尾的字符A对齐,再比较后面的字符是否和原字符串匹配。如下所示:
原字符串:ABCDA X???????
子字符串:ABCDA B //B与X不相等
结尾与开头重复字符数量:1,移动4位变成
原字符串:ABCDA X ???????
子字符串: A B CDA B //是不是发现移动后,还是比较B和X是否相等?这里是不是可以改进?(现在请忽视)
- 当我们匹配到了第7个字符
"ABCDABD"的时候,发现不匹配,而前6个字符"ABCDAB"是已经匹配成功了的,这时我们可以还是移动4位,让开头的字符AB与结尾的字符AB对齐,再比较后面的字符C是否和原字符串后面的字符相匹配。如下所示:
原字符串:ABCDAB ???????
子字符串:ABCDAB D
结尾与开头重复字符数量:2,移动4位变成:
原字符串:ABCDAB ? ??????
子字符串: AB C DABD //直接比较第3位的C是否和原字符串的?是否相等
说到这里,其实我们想要解决的问题就是:
在匹配失败的时候,怎么根据已经匹配过的字符的信息来决定往后移动多少位再重新进行匹配?
所以,我们接下来要做的事就是将上面对"ABCDABD"子字符串进行分析的过程总结出一个规律来,这也是部分匹配表的由来。如下图所示:
部分匹配值也就是结尾字符与开头字符相等的数量,比如"ABCDAB"部分匹配值就是2,"AB"是重复的。并且可以推断出
移动位数 = 已匹配的字符数 - 对应的部分匹配值
将这些部分匹配值存到数组里,则变成了next数组。
next数组的求解思路
next数组的求解的关键思想在于:
利用前面的next值去求下一个next值
举个栗子:
如果next[i-1]对应的字符串是"ABABCABAB",此时next[i-1] = 4,代表最后4个字符"ABAB"和前4个字符是重复的。
假如next[i]对应的字符串是"ABABCABABC",即最后一个字符"C"跟上一次匹配成功的字符"ABAB"的下一个字符"C"相等,则匹配值在原来的next值上+1,即
next[i] = next[i-1]+1假如next[i]对应的字符串是"ABABCABABD",即最后一个字符"D"跟上一次匹配成功的字符"ABAB"的下一个字符"C"不相等,我们可以观察出来匹配值
next[i] = 0。那是不是意味着求next[i]的值只要看A[i]与A[next[i-1]]是否相等就能得出next[i]的值是next[i-1]+1或者是0了呢?假如next[i]对应的字符串是"ABABCABABA",最后一个字符"A"跟上一次匹配成功的字符"ABAB"的下一个字符"C"也不相等,但我们能观察的出来匹配值
next[i] = 3而不是0。这里面藏着什么猫腻呢?
实际上,next[i-1]里保存的是i-1位置的最长公共前缀后缀的长度,比如字符串ABABCABAB,最长公共前缀后缀长度为4,也就是ABAB。但AB也是它的公共前缀后缀,只不过不是最长的罢了。所以,在上述的情况3中,当最后一个字符A匹配不成功时,我们还可以抢救一下它,退而求其次。既然想找理想的最长的公共前缀后缀失败,那就期望一下稍短一些的公共前缀后缀去匹配,那具体是去匹配多长的字符呢?
对于位置i-1而言,公共前缀后缀的长度依次为:next[i-1], next[next[i-1]-1], next[next[next[i-1]-1]-1]......
还是以ABABCABAB为例,next[8] = 4, 最长公共前缀后缀为ABAB;next[next[8]-1] = next[3] = 2,次长公共前缀后缀为AB;next[next[3]-1] = next[1] = 0,说明最短的公共前缀后缀就是AB了,长度为2。
代码如下:
public static int[] getNext(String pattern) {
int N = pattern.length();
int next[] = new int[N + 1];
next[1] = 0;//显然字符串的第1个字符的最大前后缀长度为0
int k =0;//最大公共前后缀长度
for (int i = 1; i < N; i++) {
while(k > 0 && pattern.charAt(i) != pattern.charAt(k))
k = next[k-1];
if(pattern.charAt(i) == pattern.charAt(k)){
k++;
}
next[i] = k;
}
return next;
}
上面代码里可能最难理解的就是for循环里的那个while循环了。其实这个while循环就是
上面所述的去匹配公共前缀后缀的过程,如果最长next[i-1]长度的没匹配到,就匹配稍短一点的next[next[i-1]-1],还没匹配到,就匹配更短一点的next[next[next[i-1]-1]-1]......直到实在是找不到公共前缀后缀了,也就是长度为0的时候,就跳出循环了。
KMP算法实现
先直接贴代码:
/**
* 在original字符串里查找子字符串find的位置
* @param original 原始字符串
* @param find 待匹配字符串
* @return 查找成功则返回匹配的首字符索引位置,否则返回-1
*/
public static int indexOf(String original, String find) {
int next[] = getNext(find);
int j = 0;
for (int i = 0; i < original.length(); i++) {
while (j > 0 && original.charAt(i) != find.charAt(j))
j = next[j-1];
if (original.charAt(i) == find.charAt(j))
j++;
if (j == find.length()) {
return i - j + 1;
}
}
return -1;
}
上面代码里可能最不容易理解的就是内部的while循环了:
while (j > 0 && original.charAt(i) != find.charAt(j))
j = next[j];
其实这个过程就是在根据部分匹配值来移动子字符串find的比较位置,跟我们最开始分析KMP原理的步骤是一样的。同样的,我们还是来举个栗子:
假如原字符串original是AACDABEAACDAADEF,待匹配的子字符串find是AACDAAD
在依次匹配字符的过程中,当i=5, j=5时,出现第一次不字符不匹配:
original.charAt(5) != find.charAt(5) //即 'B' != 'A'
AACDA B EAACDAADEF
AACDA A D
这时执行循环里的语句,j = next[j] = next[5] = 1; 这就意味着再次比较original.charAt(i) != find.charAt(j)的时候,变成了下面这样:
AACDA B EAACDAADEF
A A CDAAD // j=1,find.charAt(j) = 'A'
这就意味着将子字符串往后移动了4位,即移动位数4 = 已匹配的字符数5 - 对应的部分匹配值1
好的,KMP算法就到此结束了。~(~ ̄▽ ̄)~
更多思考
在前面移位的时候,我们举的栗子如下:
原字符串:ABCDA X???????
子字符串:ABCDA B //B与X不相等
结尾与开头重复字符数量:1,移动4位变成
原字符串:ABCDA X ???????
子字符串: A B CDA B //是不是发现移动后,还是比较B和X是否相等?
可能大家看到这个栗子的时候也有点奇怪,既然移动后,还是比较B和X,可我们在移动前就已经比较过了,是不相等的。所以这里是不是可以再往后多移2位?
也就是说这里不用匹配成功了的ABCDA的匹配值1,而是使用当前匹配失败了的ABCDAB的匹配值2?当然了,更多细节问题也需要考虑在内的,这只是我的一点个人想法,欢迎大家提出自己的看法、