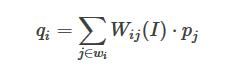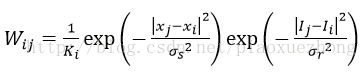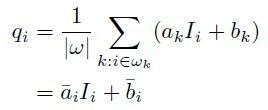guided Filter--引导滤波算法原理及实现

类似于在http://blog.csdn.net/piaoxuezhong/article/details/78302920中说的双边滤波算法，引导滤波算法也属于可以保持边缘的一种滤波算法。导向滤波之所以叫这个名字，大概是因为算法在进行滤波时需要一幅引导图像，引导图像可以是另外单独的图像，也可以是输入图像本身，当引导图为输入图像本省时，引导滤波就成为一个保持边缘的滤波操作。引导滤波可以用于降噪、细节平滑、HDR压缩、抠图、去雾以及联合采样等方面[1]。

相关算法比较：

像高斯滤波等线性滤波算法所用的核函数相对于待处理的图像是独立无关的，也就意味着，对任意图像都是采用相同的操作。但是，有时候我们是希望在滤波过程中可以加入引导图像中的信息的，例如，在上色处理过程中[2]，结果图像的色度通道需要包含跟给定亮度通道一致的连续边缘。

方式1：通过引导图像获得约束条件，转化为非齐次方程的求解问题，此方法设计到大型稀疏方程求解，所以会比较耗时。
方式2：直接利用引导图像得到滤波核函数。例如在之前说的双边滤波[3]中，在某像素点的输出为周边像素与该点相似度相关的权重和，只是双边滤波所用的引导图像是它本身；另外，在[4]中，引导图像则是另外一幅图像。
当然这些方法也有缺点：一是可能引入梯度反转伪影，二是计算量的快速优化难度。在[5]中，作者证明了双边滤波可以是一种解决高斯亲和矩阵时的雅克比插值，这就比原始优化方法在速度上要优化不少；针对这些缺点，引导滤波算法做出了改进。

引导滤波算法原理：

在通常的线性旋转变化滤波过程中，某像素点的输出为：

                               （1）

Wij为权重，在双边滤波中，其权重函数表示为：

     （2）

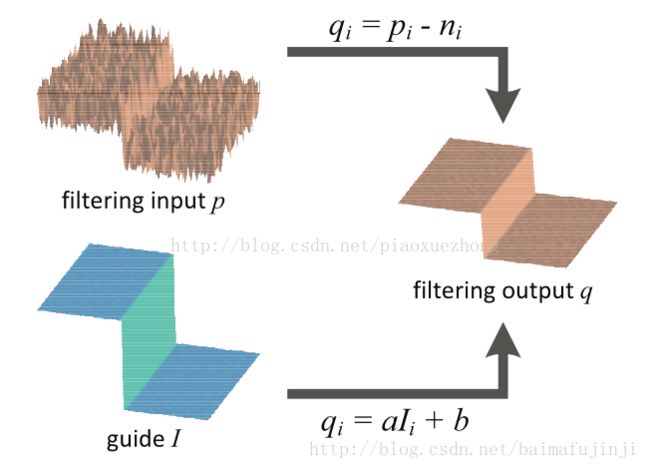
而这里要说的引导滤波，某像素点的输出结果为：

                                 （3）

其中，q 为输出图像，I 为引导图像，a 和 b 是当窗口中心位于 k 时该线性函数的不变系数。该方法的假定条件是： q 与 I 在以像素 k 为中心的窗口中存在局部线性关系。对式子（3）求导（即表示边缘）可以看出，只有当引导图像存在边缘时，输出结果才会出现边缘。为了求解（3）中的系数a和b，假设p是q滤波前的结果，并满足使得q与p的差别最小，根据无约束图像复原的方法可以转化为求最优化问题，其价值函数为(4)：

（n为噪声，p是q受到噪声n污染的退化图像）

   （4）

限制 i 在窗口 w 中，这样 a 值就不会出现太大的情况了。类似于最下二乘法求解，式（4）的解为：

其中，μ和σ^2分别表示 I 在局部窗口w 中的均值和方差。 |ω|是窗口内的像素个数。然后，在整幅图像内采取窗口操作，最后取均值可以得到式（3）的结果为：

       （5）

其中，，

总结：导引图像 I 与 q 之间存在线性关系，这样设定可以使导引图像提供的信息主要用于指示哪些是边缘。如果导引图告诉我们这里是边缘，最终的结果就设法保留这些边缘信息。所以，引导滤波的前提条件是：当I和q满足线性关系才有意义。

引导滤波算法实现：

引导滤波现在已经集成到matlab和opencv的新版本中，在matlab中函数名为：guidedfilter。opencv中的实现跟matlab应该是一样的，我在这里贴下matlab的源码：

function q = guidedfilter(I, p, r, eps)
%   GUIDEDFILTER   O(1) time implementation of guided filter.
%
%   - guidance image: I (should be a gray-scale/single channel image)
%   - filtering input image: p (should be a gray-scale/single channel image)
%   - local window radius: r
%   - regularization parameter: eps

    [hei, wid] = size(I);
    N = boxfilter(ones(hei, wid), r); % the size of each local patch; N=(2r+1)^2 except for boundary pixels.
    % imwrite(uint8(N), 'N.jpg');
    % figure,imshow(N,[]),title('N');
    mean_I = boxfilter(I, r) ./ N;
    mean_p = boxfilter(p, r) ./ N;
    mean_Ip = boxfilter(I.*p, r) ./ N;
    cov_Ip = mean_Ip - mean_I .* mean_p; % this is the covariance of (I, p) in each local patch.

    mean_II = boxfilter(I.*I, r) ./ N;
    var_I = mean_II - mean_I .* mean_I;

    a = cov_Ip ./ (var_I + eps); % Eqn. (5) in the paper;
    b = mean_p - a .* mean_I; % Eqn. (6) in the paper;

    mean_a = boxfilter(a, r) ./ N;
    mean_b = boxfilter(b, r) ./ N;

    q = mean_a .* I + mean_b; % Eqn. (8) in the paper;
end

在其实现流程中有个boxfilter函数，它是基于积分图算法实现的，boxfilter中每个元素的值是该像素邻域内的像素和（或像素平方和），在需要求某个矩形内像素和的时候，直接访问数组中对应的位置就可以了，它的复杂度是O(1)，具体可以参见【6】的讲解。或者看下boxfilter的源码：

function imDst = boxfilter(imSrc, r)

%   BOXFILTER   O(1) time box filtering using cumulative sum
%
%   - Definition imDst(x, y)=sum(sum(imSrc(x-r:x+r,y-r:y+r)));
%   - Running time independent of r; 
%   - Equivalent to the function: colfilt(imSrc, [2*r+1, 2*r+1], 'sliding', @sum);
%   - But much faster.

[hei, wid] = size(imSrc);
imDst = zeros(size(imSrc));

%cumulative sum over Y axis
imCum = cumsum(imSrc, 1);
%difference over Y axis
imDst(1:r+1, :) = imCum(1+r:2*r+1, :);
imDst(r+2:hei-r, :) = imCum(2*r+2:hei, :) - imCum(1:hei-2*r-1, :);
imDst(hei-r+1:hei, :) = repmat(imCum(hei, :), [r, 1]) - imCum(hei-2*r:hei-r-1, :);

%cumulative sum over X axis
imCum = cumsum(imDst, 2);
%difference over Y axis
imDst(:, 1:r+1) = imCum(:, 1+r:2*r+1);
imDst(:, r+2:wid-r) = imCum(:, 2*r+2:wid) - imCum(:, 1:wid-2*r-1);
imDst(:, wid-r+1:wid) = repmat(imCum(:, wid), [1, r]) - imCum(:, wid-2*r:wid-r-1);
end

引导滤波的算法伪代码：

测试函数：

%% 灰度图引导滤波
clc,clear all,close all;
I=imread('D:\fcq_proMatlab\test_image\15.jpg');
if length(size(I))>2
    I=rgb2gray(I);
end
I = double(I) / 255;
p = I;
r = 3; 
eps = 0.8^2; 
O = guidedfilter(I, p, r, eps);
figure,
subplot(1,2,1), imshow(I);
subplot(1,2,2), imshow(O);

参考：

1. 《Guided Image Filtering》[J] IEEE
2. 《Colorization using optimization》[J] In: SIGGRAPH
3. 《Bilateral filtering for gray and color images》[C] ICCV
4. 《Digital photography with flash and no-flash image pairs》[J] In: SIGGRAPH
5. 《On the origin of the bilateral filter and ways to improve it》[J] IEEE
6. http://www.cnblogs.com/easymind223/archive/2012/11/13/2768680.html
   
7. http://blog.csdn.net/zwlq1314521/article/details/51007943
8. http://blog.csdn.net/baimafujinji/article/details/74750283
9. http://blog.csdn.net/pi9nc/article/details/26592377
10. http://blog.csdn.net/lg1259156776/article/details/51815825