分类模型评估之ROC-AUC曲线和PRC曲线
http://blog.csdn.net/pipisorry/article/details/51788927
ROC曲线和AUC
ROC（Receiver Operating Characteristic，接受者工作特征曲线）曲线和AUC常被用来评价一个二值分类器（binary classifier）的优劣。博文介绍ROC和AUC的特点，讨论如何作出ROC曲线图以及计算AUC。
AUC是现在分类模型，特别是二分类模型使用的主要离线评测指标之一。相比于准确率、召回率、F1等指标，AUC有一个独特的优势，就是不关注具体得分，只关注排序结果，这使得它特别适用于排序问题的效果评估，例如推荐排序的评估。AUC这个指标有两种解释方法，一种是传统的“曲线下面积”解释，另一种是关于排序能力的解释。例如0.7的AUC，其含义可以大概理解为：给定一个正样本和一个负样本，在70%的情况下，模型对正样本的打分高于对负样本的打分。可以看出在这个解释下，我们关心的只有正负样本之间的分数高低，而具体的分值则无关紧要。
一个ROC曲线的示例
正如我们在这个ROC曲线的示例图中看到的那样，ROC曲线的横坐标为false positive rate（FPR），纵坐标为true positive rate（TPR）（也就是recall）。下图中详细说明了FPR和TPR是如何定义的。
接下来我们考虑ROC曲线图中的四个点和一条线。
第一个点，(0,1)，即FPR=0, TPR=1，这意味着FN（false negative）=0，并且FP（false positive）=0。Wow，这是一个完美的分类器，它将所有的样本都正确分类。
第二个点，(1,0)，即FPR=1，TPR=0，类似地分析可以发现这是一个最糟糕的分类器，因为它成功避开了所有的正确答案。
第三个点，(0,0)，即FPR=TPR=0，即FP（false positive）=TP（true positive）=0，可以发现该分类器预测所有的样本都为负样本（negative）。
第四个点（1,1），分类器实际上预测所有的样本都为正样本。经过以上的分析，我们可以断言，ROC曲线越接近左上角，该分类器的性能越好。
下面考虑ROC曲线图中的虚线y=x上的点。这条对角线上的点其实表示的是一个采用随机猜测策略的分类器的结果(FP = TN, TP = FN，这样FP+TP = TN + FN，即Y = N，也就是随机猜测了)，例如(0.5,0.5)，表示该分类器随机对于一半的样本猜测其为正样本，另外一半的样本为负样本。
如何画ROC曲线
通过调整模型预测的阈值可以得到不同的点，将这些点可以连成一条曲线，这条曲线叫做接受者工作特征曲线(Receiver Operating Characteristic Curve，简称ROC曲线）。
对于一个特定的分类器和测试数据集，显然只能得到一个分类结果，即一组FPR和TPR结果，而要得到一个曲线，我们实际上需要一系列FPR和TPR的值，这又是如何得到的呢？我们先来看一下Wikipedia上对ROC曲线的定义：
In signal detection theory, a receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied.
问题在于“as its discrimination threashold is varied”。如何理解这里的“discrimination threashold”呢？我们忽略了分类器的一个重要功能“概率输出”，即表示分类器认为某个样本具有多大的概率属于正样本（或负样本）。通过更深入地了解各个分类器的内部机理，我们总能想办法得到一种概率输出。通常来说，是将一个实数范围通过某个变换映射到(0,1)区间3。
假如我们已经得到了所有样本的概率输出（属于正样本的概率），现在的问题是如何改变“discrimination threashold”？我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率4。
接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：
当我们将threshold设置为1和0时，分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来，就得到了ROC曲线。当threshold取值越多，ROC曲线越平滑。
其实，我们并不一定要得到每个测试样本是正样本的概率值，只要得到这个分类器对该测试样本的“评分值”即可（评分值并不一定在(0,1)区间）。评分越高，表示分类器越肯定地认为这个测试样本是正样本，而且同时使用各个评分值作为threshold。我认为将评分值转化为概率更易于理解一些。
AUC值的计算
AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。
在了解了ROC曲线的构造过程后，编写代码实现并不是一件困难的事情。相比自己编写代码，有时候阅读其他人的代码收获更多，当然过程也更痛苦些。在此推荐scikit-learn中关于计算AUC的代码。
AUC值的高低意味着什么
那么AUC值的含义是什么呢？根据(Fawcett, 2006)，AUC的值的含义是：> The AUC value is equivalent to the probability that a randomly chosen positive example is ranked higher than a randomly chosen negative example.
这句话有些绕，我尝试解释一下：首先AUC值是一个概率值，当你随机挑选一个正样本以及一个负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然，AUC值越大，当前的分类算法越有可能将正样本排在负样本前面，即能够更好的分类。
AUC值越大的分类器，正确率越高。
从AUC判断分类器（预测模型）优劣的标准：
Concerning the AUC, a simple rule of thumb to evaluate a classifier based on this summary value is the following:
- .90-1 = very good (A)
- .80-.90 = good (B)
- .70-.80 = not so good (C)
- .60-.70 = poor (D)
- .50-.60 = fail (F)
AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测，因此不存在AUC < 0.5的情况。
图5.用AUC来衡量不同分类器的分类能力(更准确的说是排序能力)
AUC能达到多高？
对于AUC，我们只知道它是介于0和1之间的，对于一个问题，AUC具体能达到多高，好像我们从来不在乎，一般只是用一些“行业经验值”来判断自己模型的AUC够不够高。但是如果不知道理论上AUC能达到多高的话，我们就也无法准确得知当前得到的AUC究竟是高是低。就好像同样是考了90分，在100分满分的制度下和150分满分的制度下，含义是完全不同的。
理论最高AUC（Max AUC）
影响Max AUC的因素
影响这个概念的主要因素：样本的不确定性。所谓样本的不确定性，指的是对于完全相同的样本，也就是特征取值完全相同的样本，其对应的标签是否存在不确定性。
Max AUC和样本的这种样本中的不确定性，是“上帝视角分类器”也无能为力的，如果从优化问题的角度来看的话，属于不可优化的部分。
贝叶斯错误率（Bayes Error Rate，BER）
统计学中还有另外一个概念，和“不可优化”这个思想不谋而合，那就是贝叶斯错误率（Bayes Error Rate，以下简称为BER）。BER的具体定义大家可以去查看Wikipedia或者其他资料，如果用一句话来概括其思想的话，可以这么说：BER指的是任意一个分类器在一个数据集上能取得的最低的错误率。而这个错误率，则对应着数据中的不可约错误（irreducible error），也就是我们刚刚说到的“上帝视角也无法解决的错误”，“必须犯的错误”。
三种比较
| 数据集/指标 | 真实AUC |
Max AUC |
BER |
数据集1 |
0.753 |
0.971 |
0.033 |
数据集2 |
0.744 |
0.999 |
0.009 |
[多高的AUC才算高？]
为什么使用ROC曲线
一个分类模型的分类结果的好坏取决于以下两个部分：
- 分类模型的排序能力(能否把概率高的排前面，概率低的排后面)
- threshold的选择
使用AUC来衡量分类模型的好坏，可以忽略由于threshold的选择所带来的影响，因为实际应用中，这个threshold常常由先验概率或是人为决定的。
与PR曲线相比选择ROC原因见后面的对比部分。
[ROC和AUC介绍以及如何计算AUC]
[Roc曲线的两个良好特性《Beautiful Properties Of The Roc Curve》]
皮皮blog
精度-召回率曲线PRC curve
F1（计算公式略）当P和R接近就也越大，一般会画连接(0,0)和(1,1)的线，线和PRC重合的地方的F1是这条线最大的F1（光滑的情况下），此时的F1对于PRC就好象AUC对于ROC一样。一个数字比一条线更方便调模型。
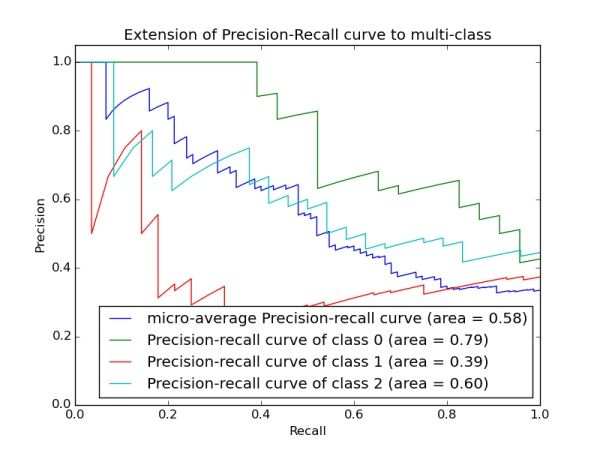以上两个指标用来
有时候模型没有单纯的谁比谁好（比如图二的蓝线和青线），选择模型还是要结合具体的使用场景。
下面是两个场景：
1. 地震的预测
对于地震的预测，我们希望的是RECALL非常高，也就是说每次地震我们都希望预测出来。这个时候我们可以牺牲PRECISION。情愿发出1000次警报，把10次地震都预测正确了；也不要预测100次对了8次漏了两次。
2. 嫌疑人定罪
基于不错怪一个好人的原则，对于嫌疑人的定罪我们希望是非常准确的。及时有时候放过了一些罪犯（recall低），但也是值得的。
对于分类器来说，本质上是给一个概率，此时，我们再选择一个CUTOFF点（阀值），高于这个点的判正，低于的判负。那么这个点的选择就需要结合你的具体场景去选择。反过来，场景会决定训练模型时的标准，比如第一个场景中，我们就只看RECALL=99.9999%（地震全中）时的PRECISION，其他指标就变得没有了意义。
如果只能选一个指标的话，肯定是选PRC了。可以把一个模型看的一清二楚。
皮皮blog
ROC曲线的PRC曲线的区别和联系
ROC曲线和PR曲线的关系
在ROC空间，ROC曲线越凸向左上方向效果越好。与ROC曲线左上凸不同的是，PR曲线是右上凸效果越好。
ROC和PR曲线都被用于评估机器学习算法对一个给定数据集的分类性能，每个数据集都包含固定数目的正样本和负样本。而ROC曲线和PR曲线之间有着很深的关系。
定理1：对于一个给定的包含正负样本的数据集，ROC空间和PR空间存在一一对应的关系，也就是说，如果recall不等于0，二者包含完全一致的混淆矩阵。我们可以将ROC曲线转化为PR曲线，反之亦然。
定理2：对于一个给定数目的正负样本数据集，一条曲线在ROC空间中比另一条曲线有优势，当且仅当第一条曲线在PR空间中也比第二条曲线有优势。（这里的“一条曲线比其他曲线有优势”是指其他曲线的所有部分与这条曲线重合或在这条曲线之下。）
证明过程见文章《The Relationship Between Precision-Recall and ROC Curves》
ROC曲线和PRC曲线的对比
ROC曲线相对的优势
既然已经这么多评价标准，为什么还要使用ROC和AUC呢？因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。下图是ROC曲线和Precision-Recall曲线的对比：
在上图中，(a)和(c)为ROC曲线，(b)和(d)为Precision-Recall曲线。(a)和(b)展示的是分类其在原始测试集（正负样本分布平衡）的结果，(c)和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而Precision-Recall曲线则变化较大。
也就是
PR曲线会面临一个问题，当需要获得更高recall时，model需要输出更多的样本，precision可能会伴随出现下降/不变/升高，得到的曲线会出现浮动差异（出现锯齿），无法像ROC一样保证单调性。
real world data经常会面临class imbalance问题，即正负样本比例失衡。根据计算公式可以推知，在testing set出现imbalance时ROC曲线能保持不变，而PR则会出现大变化。引用图(Fawcett, 2006)，(a)(c)为ROC，(b)(d)为PR，(a)(b)样本比例1:1，(c)(d)为1:10。
结论：AUC用得比较多的一个重要原因是，实际环境中正负样本极不均衡，PR曲线无法很好反映出分类器性能，而ROC受此影响小。
当正负样本差距不大的情况下，ROC和PR的趋势是差不多的，但是当负样本很多的时候，两者就截然不同了，ROC效果依然看似很好，但是PR上反映效果一般。解释起来也简单，假设就1个正例，100个负例，那么基本上TPR可能一直维持在100左右，然后突然降到0.如图，(a)(b)分别为正负样本1:1时的ROC曲线和PR曲线，二者比较接近。而(c)(d)的正负样本比例为1:1，这时ROC曲线效果依然很好，但是PR曲线则表现的比较差。这就说明PR曲线在正负样本比例悬殊较大时更能反映分类的性能。
在正负样本分布得极不均匀(highly skewed datasets)的情况下，PRC比ROC能更有效地反应分类器的好坏。
单从图a看，这两个分类器都接近完美(非常接近左上角)。图b对应着相同分类器的PR space。而从图b可以看出，这两个分类器仍有巨大的提升空间。那么原因是什么呢？ 通过看Algorithm1的点 A，可以得出一些结论。首先图a和b中的点A是相同的点，只是在不同的空间里。因为TPR=Recall=TP/(TP+FN)，换言之，真阳性率(TPR)和召回率(Recall)是同一个东西，只是有不同的名字。所以图a中TPR为0.8的点对应着图b中Recall为0.8的点。
假设数据集有100个positive instances。由图a中的点A，可以得到以下结论：TPR=TP/(TP+FN)=TP/actual positives=TP/100=0.8，所以TP=80由图b中的点A，可得：Precision=TP/(TP+FP)=80/(80+FP)=0.05，所以FP=1520再由图a中点A，可得：FPR=FP/(FP+TN)=FP/actual negatives=1520/actual negatives=0.1，所以actual negatives是15200。
由此，可以得出原数据集中只有100个positive instances，却有15200个negative instances！这就是极不均匀的数据集。直观地说，在点A处，分类器将1600 (1520+80)个instance分为positive，而其中实际上只有80个是真正的positive。 我们凭直觉来看，其实这个分类器并不好。但由于真正negative instances的数量远远大约positive，ROC的结果却“看上去很美”。所以在这种情况下，PRC更能体现本质。
结论： 在negative instances的数量远远大于positive instances的data set里， PRC更能有效衡量分类器的好坏。
References:Davis, Jesse, and Mark Goadrich. "The relationship between Precision-Recall and ROC curves." Proceedings of the 23rd International Conference on Machine Learning (ICML). ACM, 2006.
总结：
看完是不是觉得很懵逼？优势可以看成劣势。所以依lz看，如果ROC曲线面积差不多时，当然使用PRC曲线来比较两个分类算法的好坏；反之亦然。如果ROC和PRC都差不多的话那就看测试集上的PRC吧。毕竟PRC和ROC可以相互转化有很大关联的（见前面的“ROC曲线和PR曲线的关系”）。
但是lz建议在样本不均衡时最好使用ROC曲线来评估，更准确也是业内常用的。prc可能也可以，但是绝对不能只使用precision或者recall！
[精确率、召回率、F1 值、ROC、AUC 各自的优缺点是什么？]
from: http://blog.csdn.net/pipisorry/article/details/51788927
ref: [Scikit-learn：模型评估Model evaluation ]
[AUC与ROC - 衡量分类器的好坏]