经典算法（3）：动态时间规整算法（DTW）

基本DTW算法

音乐信号处理里，在同步两个音乐片段的时候，会用到动态时间规整算法。

百度了一下，语音识别里面，Dynamic Time Warping （DTW）也是必不可少的。

以下摘自百度百科。

一次正确的发音应该包含构成该发音的全部音素以及正确的音素连接次序。

其中各音素持续时间的长短与音素本身以及讲话人的状况有关。

为了提高识别率，克服发同一音而发音时间长短的不同，采用对输入语音信号进行伸长或缩短直到与标准模式的长度一致。

这个过程称为时间规整。

以下摘自一本经典书籍。

As said above, the objective of DTW is to compare two sequences of length N and Y of length M.

Going beyond the music synchronization scenario, these sequences may be discrete signals,

feature sequences, sequences of characters, or any kind of time series. Often the indices of the

sequences correspond to successive points in time that are spaced at uniform time intervals.

这里还是有一系列“特征”之间的距离度量。比如，L1距离，L2距离，cos距离……

cos距离有一个好处，消除了两个特征自身的大小（norm of the vector）。

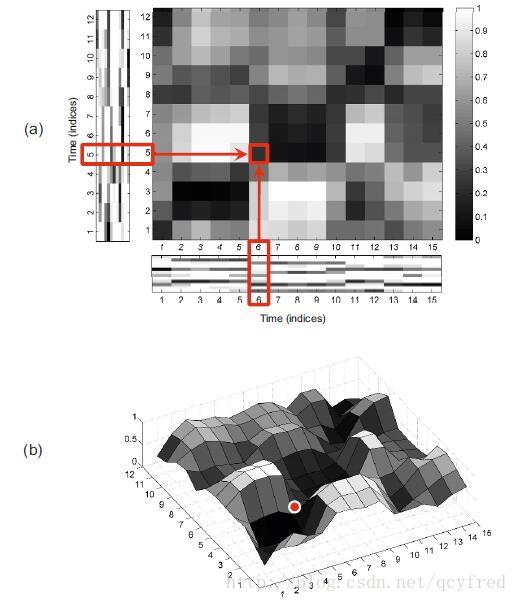
这张图画得特别形象！

In this visualization, cells of low cost are depicted in dark colors and cells of high cost in
light colors. Since the two sequences show a similar overall progression, except for 

a global difference in tempo, the cost matrix has low values along the diagonal of the matrix.

因为两个时间序列除了节拍快慢会有一些区别，总体来说还是比较相似的，所以：

总体来看，在C矩阵对角线附近值会比较低。

如果参与计算代价矩阵C的两个时间序列是同一个的话，这个矩阵就是自相似矩阵（Self Similarity Matrix）了。SSM也很有用……

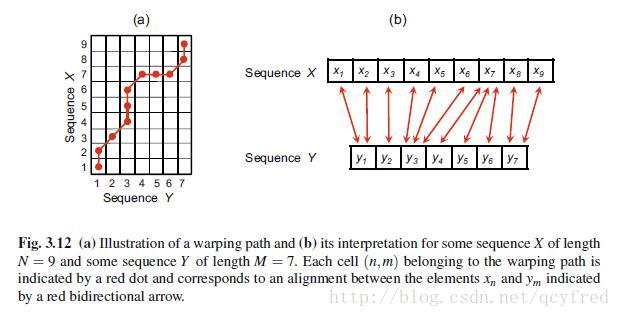
现在需要找到一条路径，让X和Y在时间上，同步（规整）一下。

规整路径，需要满足几个条件。

1. 边界条件。起点在（1，1），终点在（N，M）。因为时间序列X和Y的长度分别是N和M。

2. 单调条件。不能往回走！

3. 步长条件。这是基础DTW算法，可能的前进走法最多有3种。

The step size condition expresses a kind of continuity condition: no element in X and Y can be omitted, 

表达了一种连续性，每一个时刻的元素都得用上，不能忽略任何一个。

and there are no replications in the alignment (in the sense that all index pairs contained in a warping path P are pairwise distinct).

并且在代价矩阵中，每一次都不能停留在原来的点上。在路径P中，不能有相同的坐标点。

什么才叫DTW的最优路径？

路径是一系列坐标值，在路径中的每一个点上，有此时此刻的一个代价（二元数量值函数的自变量与函数值的关系）。

这条路径最优，等价于路径所付出的总的代价最小。意思就是，这样规整，总的差异最小。

怎么找最优路径？

这和Viterbi译码很像。

不可能蛮干，找出所有的路径。情况太多，计算量太大。（However, the number of different (N,M)-warping paths is exponential in N and M）

可以用动态规划dynamic programming，大幅度减小计算量。O（NM）。

The general idea behind dynamic programming is to break down a given problem into simpler subproblems 

and then to combine the solutions of the subproblems to reach an overall solution. 

In the case of DTW, the idea is to derive an optimal warping path for the original sequences from 

optimal warping paths for truncated subsequences. This idea can then be applied recursively.

递归实现…（凡是递归的，都可以用非递归的方式去写）

递归太难搞了…

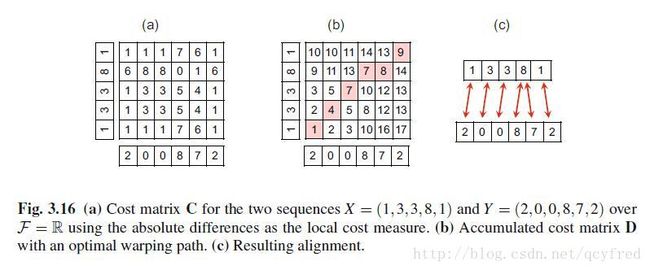
引入一个累计代价矩阵D，矩阵的（m,n）元素代表在最优路径中从（1,1）到（m,n）的累计代价。

Each value D(n,m) specifies the total (or accumulated) cost of an optimal warping path starting at cell (1,1) and ending at cell (n,m).

D是可以递归计算。

根据这个D，就可以从后（M，N）往前（1，1），找某个邻域内，最小的D所对应的元素坐标（m，n）了。

这样，就可以找到最优路径。据说，这种算法的计算复杂度是O（MN）。

backtracking！只能从后往前！从前往后找不到！

用Vertibi算法找HMM里最大概率路径，也用了类似的方法！

感觉，引入矩阵D，就是在用空间换时间，

同时，用更大的空间，让实现思路更简单……

把书本关上，如何回忆这种算法？（不要开卷了然，闭卷茫然…）

用草稿纸上，画一画，就能把C和D这两个矩阵是怎么来的，写清楚。

然后就是找路径。反着找。从D（M，N）开始，因为P（L） = （M，N），终点。

然后，一直找它相邻3个元素D(m，n-1)，D（m-1，n），D（m-1，n-1）里，最小的那个数对应的其坐标就是最优路径中的一个点。

当路径碰到D的边界的时候（m==1或n==1），下一个路径的m（或n）还是要等于1了，然后顺着边界继续走就是了。

终止条件：直到路径中出现了（1，1）起点。

注：当找最小的元素有相同的时候，按理说可以任意取一个嘛…推荐说取字典序最小的那个。

最后，反着输出最优路径，就OK。

用书上的例子。

% Basic Dynamic Time Warping
% 作者：qcy
% 时间：2016年5月18日13:49:32（此时正在上分布式计算…）
% 版本：v1.0

clear;
close all;
clc

x = [1,3,3,8,1];
y = [2,0,0,8,7,2];

[ C,D,P,DV ] = dtw3( x,y );

%% 打印输出路径
idxs = [];
idys = [];
for k = 1:length(P)
    idx = P(k).n;
    idy = P(k).m;
    
    fprintf('路径:%3d,%3d, 累计cost值:%6f\n',idx,idy,DV(k));
    idxs = [idxs,idx];
    idys = [idys,idy];
end


%% x和y对应!
for k = 1:max(length(x),length(y))
    fprintf('x:%5f, y:%5f\n',x(idxs(k)),y(idys(k)));
end

% Finised by qcy in Computing Center B325 @ 2016年5月18日15:25:39

function [ C,D,P,DV ] = dtw3( x,y )
%function [ C,D,P,DV ] = dtw3( x,y )

% 没有用递归。

% Algorithm: DTW
% Input: Cost matrix C of size N ×M
% Output: Accumulated cost matrix D,C,P正序路径,在正序路径上对应的累计代价的值 DV
% Optimal warping path P

% 说明：这里的 D 和书上的D ，行是反着的。从上往下，从下往上。
% 所以，后面是从右上角到左下角，而不是右下角到左上角。
% 但在写代码的过程中，序号应该和书上是一致的。

%% 1. 用X和Y，计算C

len_x = length(x);
len_y = length(y);
C = zeros(len_x,len_y);

for kx = 1:len_x
    for ky = 1:len_y
        x_temp = x(kx);
        y_temp = y(ky);
        delta = x_temp - y_temp;
        C(kx,ky) = abs(delta);
    end
end

%% 2 用C，计算出D
% 1. 对D的第一个数初始化
D = zeros(size(C));
D(1,1) = C(1,1);

% 2. 对D的各行初始化
for kx = 2:len_x
    D(kx,1) =  D(kx-1,1) + C(kx,1);
end

% 3. 对D的各列初始化
for ky = 2:len_y
    D(1,ky) = D(1,ky-1) + C(1,ky);
end

for kx = 2:len_x
    for ky = 2:len_y
        % 这一个格子，是从上一个格子的D再进一个格子来的
        D(kx,ky) = C(kx,ky) + min([D(kx-1,ky-1),D(kx-1,ky),D(kx,ky-1)]);
    end
end

l = 1; % 路径序号
q = []; % 最优路径（反向）
q(l).n = len_x; % 最优路径从（M,N）开始
q(l).m = len_y; % 最优路径从（M,N）开始

while q(l).m ~= 1 && q(l).n ~= 1  % 直到找到D（1,1）这个元素，才结束循环
    l = l + 1; % 路径序号+1
    n = q(l-1).n;
    m = q(l-1).m;
    
    if n == 1 % 到了D矩阵的边界了
        q(l).n = 1;
        q(l).m = m - 1;
    elseif m == 1 % 到了D矩阵的边界了
        q(l).n = n-1;
        q(l).m = 1;
    else % 还在D矩阵的中间
        D1 = D(n-1,m-1);
        D2 = D(n-1,m);
        D3 = D(n,m-1);
        DD = [D1, D2, D3];
        
        % DD中三个元素都相等，take lexicographically smallest cell.
        [~,k] = min(DD); % matlab的min，会用第一个最小元素的idx
        switch k
            case 1,
                q(l).n = n-1;
                q(l).m = m-1;
            case 2,
                q(l).n = n-1;
                q(l).m = m;
            case 3,
                q(l).n = n;
                q(l).m = m-1;
        end
    end
end


P = q(end:-1:1);
DV = zeros(length(P),1);
for k = 1:length(P)
    DV(k) = D(P(k).n,P(k).m);
end


%% 把D和C 从上往下 颠倒
T = D;
for kT = 1:size(D,1)
    temp = D(kT,:);
    T(end-kT+1,:) = temp;
end
D = T;

T = C;
for kT = 1:size(C,1)
    temp = C(kT,:);
    T(end-kT+1,:) = temp;
end
C = T;

end

路径:  1,  1, 累计cost值:1.000000
路径:  2,  2, 累计cost值:4.000000
路径:  3,  3, 累计cost值:7.000000
路径:  4,  4, 累计cost值:7.000000
路径:  4,  5, 累计cost值:8.000000
路径:  5,  6, 累计cost值:9.000000
x:1.000000, y:2.000000
x:3.000000, y:0.000000
x:3.000000, y:0.000000
x:8.000000, y:8.000000
x:8.000000, y:7.000000
x:1.000000, y:2.000000

变种DTW算法

有待进一步学习。