论文阅读，GAN 生成对抗网络 2014 Goodfellow原文阅读笔记

2014Generative Adversarial Nets(精读2017.3.2)

Goodfellow, Bengio et al.
NIPS2014
蒙特利尔大学

摘要

一种新的生成式框架，同时训练两个模型，一个称为“产出模型” G，另一个称为“检验模型” D
G用于描述数据的分布（或者说是生成尽可能拟合真实数据的分布），D用于对G各个迭代轮次产生的结果进行评估，D的目标是尽可能评估得出真实分布比G生成的“高仿分布”更加真实，而G的目标就是尽可能使生成的结果让D的辨认出现错误（注意，这里不同于某些解读说的：尽量生成出更真实的分布）

举一个拙劣的比喻就是：假设我们来到一家古玩店，G是一个学徒，D是他的师父，师父让学徒对着真迹造一个赝品出来，学徒尽可能早出赝品满足师父的要求，让师父的鉴别出错，无法辨认赝品和真迹，而师父则是尽可能从赝品找出蛛丝马迹来发现它其实不是真迹

摘要还提到，D最终收敛时给出的目标结果应该是 12 ，后文还会有定性和定量的分析和推理
ps：arbitrary（任意），demonstrate（证明，证实），potential（潜力 n，潜在的 adj）

引言

提到深度学习模型的优势和发展，能够对标签和分布有更加深入丰富的感知
提到深度生成模型中一个比较棘手的问题就是，类最大似然估计中复杂的概率计算，于是尝试找出一些方法来巧妙地规避这个问题
这个框架是一种minmax复合的博弈游戏

最大似然基本思想（来自百度百科）：当从模型总体随机抽取n组样本观测值后，最合理的参数估计量，应该使得从模型中抽取n组样本观测值的概率最大，而非如最小二乘法一样，旨在得到使得模型能最好地拟合样本数据的参数估计量
似然函数：

L(θ∣x)=P(X=x∣θ)

推广形式：

L(θ1,θ2,…θk)=∏i=1nP(x1;θ1,…,θk)

提出的框架适用于各种训练算法以及最优化算法，本文将在实验中使用MLP（多层感知机）作为GAN框架的实验对象，使用MLP去对噪音数据去噪，并使用MLP作为检验模型D

相关工作

提到 大多数深度生成模型是关于给出概率分布的参数模型，并使用最大似然估计
后人尝试用BP算法去代替复杂的近似估计算法[4]
深度波兹曼机就是典型的深度生成模型，似然计算复杂，于是催生出了“生成机”这种东西，避开对似然过程的准确描述，由期望的分布生成样本

提到一种随机生成网络，延伸成为本文的工作[18]
包括VAE（变分自编码机）[23]，这些模型中，BP规则成为主要的超参数
但是GAN和它们是有区别的，不同于VAE在隐式单元中描述差异性，GAN在显式单元中描述差异性，这也导致GAN不能对离散数据建模

还有一种“批判性训练”，利用标准，使用一个事先训练好的噪音分布作为“竞争对手”（这是一种非正式的竞争网络），需要估计并反向传播密度[13]，ps：解读这里的竞争对手是预定义的，没有和被训练的model一起经历训练过程

[26]用其他隐单元去描述当前隐单元的值，虽然和本文工作有一定可比性，但竞争并非其主要的训练标准，而是鼓励隐单元在完成某项任务后更加概率独立，另外一个区别就是学习规格不同

“对抗样例”是与GAN最为容易混淆的模型（其实也是他们团队提出来的），尝试找出分类失误的样例。但这个工作主要试图揭示神经网络的深层行为，并体现出某些神经网络分类模型过度自信，脱离了人类的认知

对抗网络

这一部分是给出对抗网络的基本概念，让读者有一个大致的认识
首先给出真实的数据分布 x ，G对它的描述是 pg ，另外还有一个预定义好的噪音变量 pz(z) ，模型G被定义为一个可微函数 G(z;θg) ， z 就是其输入， θg 就是其参数
所以 G:input(z),output:Pg

然后定义鉴别函数 D(x;θd) ， D:input(x),output:value ，D输出的就是一个标量，用于表示输入的 x 来自真实数据而非G的生成数据的概率，D的训练过程就是最大化概率：将正确的标签同时分配给训练样本和G的输出的概率
这里可能有疑惑，明明D就给G挑刺的，为什么还要这么训练呢？首先想一下，师父如果很水，不分青红皂白给学徒打低分，那么整个过程还有意义吗？首先要训练出一个经验丰富，很少犯错，铁面无私的师父来才对（个人理解）

而G的训练目标就是最小化 log(1−D(G(z))) ，综合的最优化问题 minGmaxDV(D,G) ，详见：式(1)
转化为最大化 log(D(G(z))) 的对偶问题，目的是让最终整体的复合最优化问题在理论上可收敛： min→←max

平衡G和D的学习率是训练过程的关键，否则会产生无休止地计算或者在有限的数据集上过拟合等等现象
训练时可能需要D和G训练过程 k:1 地交替（就是让G等D几步）

理论结论

理论论证部分能在非参数设置的情形下描述清楚，理论上GAN可以无限地学习优化下去
4.1证明框架有全局最优解 pg=pdata
4.2推导GAN算法通过最优化公式(1)能得到最优解（证明算法的收敛性）

观察示例图，4个小图中，上半个图显示的是真实分布 x ，生成模型G的输出分布，以及检验模型D的状态变化，下半个图显示的是生成分布 G(z) 被强制拟合真实分布 x 时的不平衡情况，ps：虚线 D，黑点线 实际的数据分布，实线 G
可以看到一开始D没有被训练好，混乱波动，经过训练之后，能够较为准确地评估G的输出对 x 的拟合程度，最终D的输出为 12 时（也就是 x 和 G(z) 一样），整个过程达到收敛

从算法1中可以看到，每 k 轮D的训练迭代后，经历一次G的训练迭代。D的优化过程同时接收两种数据：人造的噪音数据 pg(z) 的样本，真实数据 pdata(x) 的样本，使用随机梯度上升 →max ，G的优化过程通过BP接收D对G的评估，从而优化G。整个训练过程可以通过任何梯度学习的模式运转

关于全局最优解的讨论

命题1，首先设定D的理想形式（目标值）： pdata(x)pdata(x)+pg(x)
首先证明这个目标值的设定机理（同时也是推导内层 max 目标函数的最优化过程），将公式(1)改写为：

V(G,D)=∫xpdata(x)log(D(x))+pg(x)log(1−D(x))dx

我们先暂时忽略G，将 V(G,D) 看作D的函数，并且设 D(x)=y ，在样本空间中，对于真实的数据分布 pdata(x) 设为 a ， pg(x) 设为 b ，于是，内层的目标函数被简写成:

argmax(alog(y)+blog(1−y))

利用对数变换法则推导下去:

f(y)=log(ya(1−y)b)

因为 log 默认的底为 10 ，所以 logY 是单调递增的，于是我们把外面的 log 去掉得到： ya(1−y)b
首先要说明，概率分布肯定都是 0⩽P⩽1 的而且 y 的定义域也是 [0,1] 。我们将 a 和 b 都设定为 0.6 ，然后大家来看一下这个函数的图像：

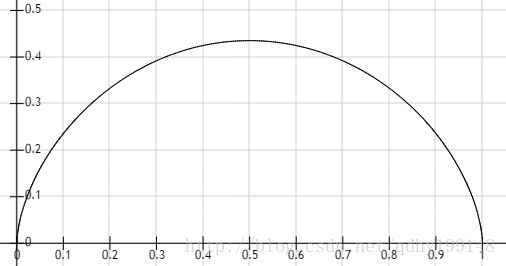
是一个下凸函数，开口向下，所以我的再对上面的公式 f(y)=ya(1−y)b 求导，并令其 =0 ：

f′(y)=[ya(1−y)b]′=aya−1(1−y)b−bya(1−y)b−1=0⟹aya−1(1−y)b=bya(1−y)b−1⟹a(1−y)=by⟹y=aa+b

到这里为止，D的最优形式就推导出来了，就是 pdata(x)pdata(x)+pg(x)
另外还有一点就是，检验函数D的优化过程可以理解为对条件概率 P(Y=y | x)的最大似然估计， y=1 时认为 x from pdata ， y=0 时，认为 x from pg
最后，内层最优化已经完成，现在我们把整体的目标函数改写成关于G的函激:

C(G)=Ex∼pdata[logpdata(x)pdata(x)+pg(x)]+Ex∼pg[logpg(x)pdata(x)+pg(x)]

然后我的开始对外层最优化过程进行推导和证明
首先给出要证明的定理1 : C(G) 在 pg=pdata 时达到最优值 −log4 ，也就是最终的 minmaxV=−log4
我们首先假定已经达到了 pg=pdata 的 平衡状态，这个时候显然 D∗G(x)=12 ，代入上面的公式，得到 C(G)=−log4
然后我们使用KL散度来衡量任意时刻 C(G) 离 平衡状态的差距：

C(G)=−log4+KL(pdata‖pdata+pg2)+KL(pg‖pdata+pg2)

KL散度又称相对摘，用于衡量两个分布之间的差异，更准确的说是某分布A去拟合另一个分布B时需要产生的损失量，所以我们知道KL散度是有指向的，也就是说，上面那条公式的第二项与第三项不一定相等
KL散度 ⩾0 ，当且仅当 KL(a‖b) 中的 a=b 时，等号成立

为了用统一的形式衡量差距，作者又进行了一次变形，这次换成了Jensen-Shannon距离:

C(G)=log4+2⋅JSD(pdata‖pg)

从JS距离的定义我们可知

JSD(a‖b)=12KL(a‖a+b2)+12KL(b‖a+b2)

所以得到了式中的 2⋅JSD(pdata‖pg)
JS.距离和KL散度一样， ⩾0 ，只有在 pdata=pg 时，等号才成立

这样就结束了证明，得到结论：只有在 pdata=pg 时， C(G) 能够达到最小值 −log4

关于算法收敛性的讨论

收敛性的证明主要是证明 pg 的优化过程能够达到全局最优解 pdata
将 V(G,D) 改写为关于 pg 的凸函数 U(pg,D) ，通过说明凸函数的次导数包含了导数，说明凸函数的优化过程最终能收敛到上面定理1已经证明的唯一全局最优解 pdata 上

实验

实验在MNIST手写数字数据集和多伦多人脸数据集，还有CIFAR-10数据集上对GAN的性能造行了检验

其他

后面还有一些关于深度生成式模型的各种优缺点什么的东西，看的论文太少，还得补补

读后思考

1. GAN里的G和D看上去互相依存，我的输出输入你，你的输出又输入给我，这显然是一个先有鸡还是先有蛋的问题，其实在Algorithm 1. 里面已经写的很清楚了，在算法的一开始，将非常粗糙的人工噪音数据 z 和真实数据 x 两次输入鉴别函数D，在最优化过程中对它们的组合计算值(算法1给出的公式里有)做最大化，这样 k 步之后（大循环内部的小循环），再开始优化G（其实没有D，G根本无法接收BP结果来优化自己，也说明了这个问题）。那么，如果没有人工噪音数据 z ，怎么解决冷启动问题？直接随机化一个 z 好了
2. 引言中还有一句很经典的话，我意译一下：BP算法和dropout机制带来了神经网络和深度学习近些年的辉煌。细想一下，确实如此

by SCUT PhD 胡杨
原文地址：https://arxiv.org/abs/1406.2661