KMP算法及其优化
先简单说一下KMP的概念:
设主串为S,匹配串为T,则
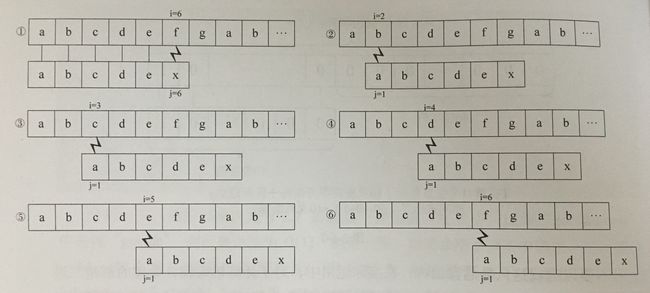
栗子Ⅰ 如图:
步骤①中 S[1~5]与T[1~5]都匹配,S[6]与T[6]不匹配
由T中可得 T[1] ≠ T[2] ≠ T[3] ≠ T[4] ≠ T[5],
然而 T[2]=S[2] , T[3]=S[3] , T[4]=S[4] , T[5]=S[5]
所以 T[1] ≠ S[1~5] ,即②③④⑤的比较都是多于的
我们只需要把 T[1] 移动到与 S[6] 匹配即刻
有人会问:要是T[1] 与后面某个字符T[j] 相等呢?
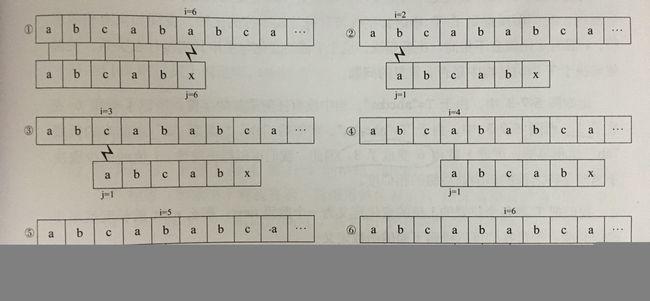
那我们就举个栗子Ⅱ
步骤①中 S[1~5]与T[1~5]都匹配,S[6]与T[6]不匹配
由T中可得 T[1] ≠ T[2] ≠ T[3] = T[4] ≠ T[5],
T[1] ≠ T[2] ≠ T[3] ≠ T[4] = T[5],
即 T[1~2] 与 T[4~5] 相等,
存在 前缀ab与后缀ab 2个字符相等。
因为 S[1~5]与T[1~5]都匹配
所以 T[1] ≠ S[2] ≠ S[3] ,即 ②③ 可以省略
又因为已经知道 T[1] = T[4] , T[2] = T[5]
所以直接拿 T[3]与S[6] 比较
所以 步骤④⑤可以省略
可以得出:
如果
字符串T中有前 j 个字符与S匹配成功, 且 T[j+1] ≠ S [i+1],
T中匹配成功的字符 T[1 ~ j ] 中,如果前后缀有 n 个字符相等,
则就从 T[n+1] 开始与 S[i+1] 比较
那么我们如何推导Next数组呢?
设T串中,
T[j]表示前缀的单个字符,
T[i]表示后缀的单个字符。
如果T[j]=T[i],则 j++ i++,next[i]=j (next记录在第i个字符匹配失败的时候,j应该回溯到哪个位置)
继续向后比较。
如果T[j]!=T[i] ,则用next数组对 j 进行回溯,回溯的原理类似 T[j]≠S[i]时候,
T[1~ i-1] 中的前缀最长有 j-1个字符 与后缀相等,
如果前缀在第 j 个位置匹配失败
则 j = next[j],对前缀进行回溯,
至于回溯的原理,j为什么等于next[j],可以对比一下上文的栗子Ⅱ
以下是 推倒next的代码,T串是从T[1]开始记录字符的
void get_next(char T,int *next){
int i,j;
i=1;
j=0;
next[1]=0;//如果第1个字符就匹配失败,则j回归0这个位置,随后和 i一起 +1,达到T串向后移动一个单位的目的。
while(i但是这样推导出的Next数组是缺陷的。
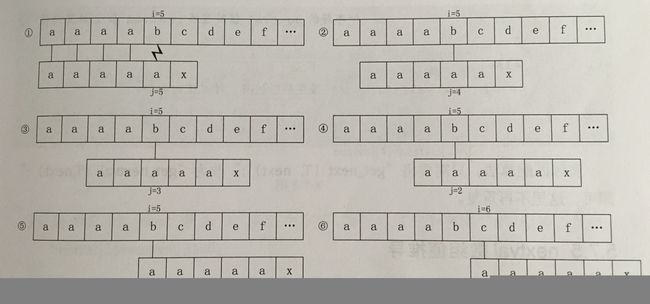
例如 S[]="aaaabcde" ,T[]="aaaaax"
按我们楼上推导next的方法,推出的next是
i= 1 2 3 4 5 6
next[i]= 0 1 2 3 4 5
所以按楼上推导出的next,匹配的时候是需要经历步骤②③④⑤的。
我们仔细观察可以发现,T[5]匹配失败的时候,即T[5]≠S[5]
可是,T[5]是等于 T[1~4]的,所以可以得出,T[1~4]≠S[5],
也就是说,我们可以省略②③④⑤。
由于T串的T[2~5]都与T[1]相等,所以我们可以用 next[1] 去取代与它相等的字符后续next[j]的值。
所以KMP是可以继续优化的
以下是优化后的代码,( T串是从T[1]开始记录字符的 )
void getNext(char T[],int next[]) {
int i, j;
j = 0;
i = 1;
next[0] = 0;
while (i < T[0]) {
if (j == 0 || T[j] == T[i]) {
j++;
i++;
if (T[i] != T[j])//若当前字符与前缀字符不同
{
next[i] = j;
}
else //若当前字符与前缀字符相同
{
next[i] = next[j];
}
}
else j = next[j];
}
}
优化后的KMP完整代码( T串是从T[0]开始记录字符的)
#include
using namespace std;
void getNext(char T[],int nt[]) {
int len, i, j;
len = strlen(T);
j = -1;
i = 0;
nt[0] = -1;
while (i < len) {
if (j == -1 || T[j] == T[i]) {
j++;
i++;
if (T[i] != T[j])nt[i] = j;
else nt[i] = nt[j];
}
else j = nt[j];
}
}
int KMP(char S[], char T[], int pos = 0) {
int slen, tlen;
slen = strlen(S);
tlen = strlen(T);
int *nt = new int[tlen];//动态创建next数组,大小为T串的大小
getNext(T, nt);
int i, j;
i = 0;
j = -1;
while (i < slen&&j < tlen) {
if (j == -1 || S[i] == T[j]) {
i++;
j++;
}
else j = nt[j];
}
if (j == tlen)return i - tlen;
return -1;
}
int main() {
char S[20], T[20];
int pos;
cin >> S >> T;
pos = KMP(S, T);
if (pos != -1)cout << pos;
else cout << "Not found !";
return 0;
}