机器学习算法——回归算法总结(一)
机器学习算法——回归算法总结(一)
回归算法与分类算法都属于监督学习算法,不同的是,分类算法中标签是一些离散值,代表不同的分类,而回归算法中,标签是一些连续值,回归算法需要训练得到样本特征到这些连续标签之间的映射。
1.线性回归
2.局部加权回归
3.岭回归
4.Lasso回归
5.CART回归树
一 线性回归:
线性回归是一类重要的回归问题,在线性回归中,目标值和特征之间存在线性相关的关系
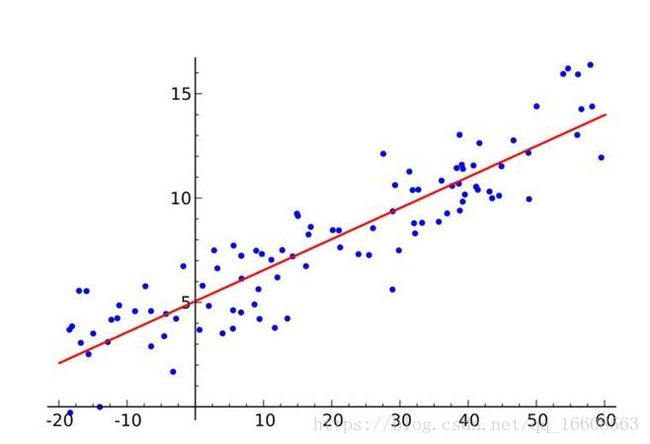
1 基本的线性回归
线性回归模型 一般有如下的线性回归方程:
y = b + ∑ i = 1 n w i x i \displaystyle\sum_{i=1}^{n}w_ix_i i=1∑nwixi 其中b为偏置 , w i w_i wi为回归系数。对于上式令 x 0 x_0 x0 =1 可以写成 y= ∑ i = 0 n w i x i \displaystyle\sum_{i=0}^{n}w_ix_i i=0∑nwixi
2 线性回归模型的损失函数
线性回归的评价是指如何度量预测值与标签之间的接近程度。线性回归模型的损失函数可以是绝对损失和平方损失
其中,绝对损失为 l = |y - y ∗ y^* y∗| 其中 y ∗ y^* y∗为预测值,且 y ∗ = ∑ i = 0 n w i x i y^*=\displaystyle\sum_{i=0}^{n}w_ix_i y∗=i=0∑nwixi
平方损失函数:l = ( y − y ∗ ) 2 (y - y^*)^2 (y−y∗)2
由于平方损失处处可导,通常使用平方误差作为线性回归模型的损失函数。
假设有m个样本,每个样本有n-1个特征,则平方误差可表示为:
l=0.5* ∑ i = 1 m ( y ( i ) − ∑ j = 0 n − 1 w j x j ( i ) ) 2 \displaystyle\sum_{i=1}^{m}(y^{(i)}-\displaystyle\sum_{j=0}^{n-1}w_jx_{j}^{(i)})^2 i=1∑m(y(i)−j=0∑n−1wjxj(i))2
对于平方误差损失函数,线性回归的求解就是希望求得平方误差的最小值。
3 线性回归的最小二乘法
预测函数可以用矩阵的方式表示:Y = WX其损失函数可以表示为:
( Y − X W ) T ( Y − X W ) (Y - XW)^T(Y -XW) (Y−XW)T(Y−XW)
对 w进行求导,得 X T ( Y − X W ) X^T(Y-XW) XT(Y−XW) 令其为零 可得 W ∗ = ( X T X ) − 1 X T Y W^*=(X^TX)^{-1}X^TY W∗=(XTX)−1XTY
利用python实现最小二乘法十分简单:
import numpy as np
def least_square(feature,label):
w = (feature.T *feature).I * feature.T * label
return w
这中方法前提是要矩阵 ( X T X ) (X^TX) (XTX)是满秩矩阵,其逆矩阵才存在
4 牛顿法求解回归系数w(重要)
牛顿法的基本思想是利用迭代点 x k x_k xk处的一介导数(梯度)和二阶导数(Hessen矩阵)对目标函数进行二次函数近似,然后把二次函数的极小值点作为新的迭代点,并不断重复这一个过程,知道求得满足精度的近似极小值。
基本牛顿法是一种基于导数的方法,它每一步的迭代方向都是沿着当前点的函数值下降方向。
对于一维的情况,对于一个需要求解的优化问题f(x),求其极值得问题,可以转换为导函数f`(x)=0.
对函数f(x)进行泰勒展开到二阶
f ( x ) = f ( x k ) + f ′ ( x k ) ( x − x k ) + 0.5 f ′ ′ ( x k ) ( x − x k ) 2 f(x)= f(x_k)+f'(x_k)(x-x_k)+0.5f''(x_k)(x-x_k)^2 f(x)=f(xk)+f′(xk)(x−xk)+0.5f′′(xk)(x−xk)2
对其求导(对x求导)得到:
f ′ ( x k ) + f ′ ′ ( x k ) ( x − x k ) f'(x_k) + f''(x_k)(x-x_k) f′(xk)+f′′(xk)(x−xk)=0 得到 x = x k − f ′ ( x k ) f ′ ′ ( x k ) x = x_k - \frac{f'(x_k)}{f''(x_k)} x=xk−f′′(xk)f′(xk)
这就是牛顿法的更新公式。
基本牛顿法流程:
1.给定终止误差值 0<ε<1 初始点 x 0 x_0 x0,令k=0;
2.计算 g k = ▽ f ( x k ) g_k= ▽f(x_k) gk=▽f(xk),若|| g k g_k gk||<= ε,则停止,输出 x ∗ = x k x^* = x_k x∗=xk
3.计算 G k = ▽ 2 f ( x k ) G_k = ▽^2f(x_k) Gk=▽2f(xk)并求解线性方程组 G k d = − g k G_kd = -g_k Gkd=−gk得解 d k d_k dk
4.令 x k + 1 = x k + d k k = k + 1 x_{k+1}=x_k + d_k k = k+1 xk+1=xk+dkk=k+1 转2
基本牛顿法的优点是收敛速度快,局部二阶收敛性,但是缺点是需要初始点需要足够靠近极小点,否则算法可能不收敛。

全局牛顿法相对于基本牛顿法其实就是引入了一个搜索步长,这个步长的确定也是通过线性搜索得到的。(具体可参考董晓辉的优化方法那本书)
牛顿法需要计算Hessen矩阵的逆矩阵,计算量太大,可以利用拟牛顿法法,拟牛顿法核心是找一个矩阵近似代替Hessen矩阵的逆矩阵
二 局部加权线性回归
当数据的全局线性回归的性质不是那么完美时,线性回归中可能出现欠拟合问题。局部加权回归可以解决这种情况。
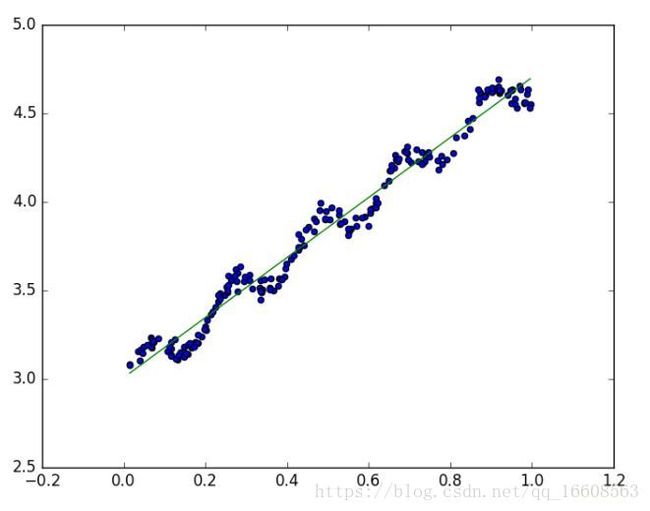
局部加权回归执行以下步骤:
1.针对给定的查询点 x x x,寻找使 ∑ i w ( i ) ( y ( i ) − θ T x ( i ) ) 2 \displaystyle\sum_{i}w(i)(y^{(i)}-\theta^Tx^{(i)})^2 i∑w(i)(y(i)−θTx(i))2取最小的 θ \theta θ
2.给出预测结果 θ T x \theta^Tx θTx
这里的 w w w称为权值,是一个非负数,直观上看,如果对于某个 i , w ( i ) i,w(i) i,w(i)取值较大,则在计算 θ \theta θ取值时,我们将尽可能的减小 ( y ( i ) − θ T x ( i ) ) 2 (y^{(i)}-\theta^Tx^{(i)})^2 (y(i)−θTx(i))2项的取值(精确拟合);反之,如果 w ( i ) w(i) w(i)取值较小,则 ( y ( i ) − θ T x ( i ) ) 2 (y^{(i)}-\theta^Tx^{(i)})^2 (y(i)−θTx(i))2所得到的误差项将足够小二忽略不计。
局部加权回归采用的是给预测点附近的每一个点赋予一定的权重,
此时的回归系数可以表示为: W = ( X T M X ) − 1 X T M Y W = (X^TMX)^{-1}X^TMY W=(XTMX)−1XTMY M是每个点的权重
LWLR使用核函数来对附近的点赋予更高的权重,常用的有高斯核,对应的权重为
M ( i , i ) = e x p ( ∣ ∣ X i − X ∣ ∣ 2 − 2 k 2 ) M(i,i)=exp(\frac{||X^i-X||^{2}}{-2k^2}) M(i,i)=exp(−2k2∣∣Xi−X∣∣2)
其中 x是查询点, x i x_i xi是第i个训练样本,k是可调参数,控制训练点到查询点的权重衰减速率。
易看出,对于给定的查询点x,权值的大小与训练样本x(i)相对于x的位置密切相关:
1)如果x(i)距离x很近,则ω(i)将取靠近1的值;
2)如果x(i)距离x很远,则ω(i)将取到0附近。
注意:尽管权值函数的样子看起来很像高斯分布的概率密度函数,但是这个函数跟高斯分布并没有直接联系,另外ω(i)并不是随机变量,也并不服从高斯分布,它只是一个样子恰好类似钟形的曲线
这样的权重矩阵只含对角元素。
def lwlr(testpoint,xArr,yArr,k=1.0):
xMat= mat(xArr)
yMat= mat(yArr)
m= shape(xMat)[0]
weights=mat(eye((m)))
for j in range(m):
diffMat = testpoint -xMat[j,:]
weights[j,j]=exp(diffMat*diffMat.T /(-2.0 *k**2)
xTx = xMat.T * (weights*xMat)
if linalg.det(xTX)==0.0:
print "This matrix is singular ,can not to inverse"
return
w = xTx.I *(xMat.T *(weights*yMat)
return testpoint * w
局部加权回归算法中,核函数的k值时唯一可调参数,当k值变小时,离测试点较远的点的权重会指数级减小,此时拟合数据的能力会变强。
局部加权线性回归算法中,我们对测试点附近的每一个点赋予一定的权重,在这个子集上基于最小均方差来进行普通的回归。
函数中的τ称作带宽(bandwidth)(或波长)参数,它控制了权值随距离下降的速率。如果τ取值较小,则会得到一个较窄的钟形曲线,这意味着离给定查询点x较远的训练样本x(i)的权值(对查询点x附近训练样本的拟合的影响)将下降的非常快;而τ较大时,则会得到一个较为平缓的曲线,于是查询点附近的训练样本的权重随距离而下降的速度就会相对比较慢。
值得注意的是,这是一个非参数算法,我们在使用这个方法时,是针对给定的查询点x进行计算,也就是每当我们对于一个给定的x做出预测时,都需要根据整个训练集重新进行拟合运算,如果训练集很大而查询很频繁的话,这个算法的代价将非常高。关于提高这个算法的效率,可以参考Andrew Moore关于KD-Tree的工作。
局部线性回归算法的问题在于,对于每一个要查询的点,都要重新依据整个数据集计算一个线性回归模型出来,这样使得计算代价极高。