【论文阅读笔记】Ristretto: Hardware-Oriented Approximation of Convolutional Neural Networks
概念
MAC:multiplication-accumulation operations
2. Convolutional Neural Networks
2.2.1 Normalization layers
正则化层(LRN、BN) 需要计算出非常多的中间数(不是参数)。以AlexNet为例,LRN层的中间数可以达到214 ,比任意层的中间数都有多。因为这个原因,这篇文章假设LRN和BN层用float point计算,而我们致力于其它层的近似。【本文只集中于近似fc层和conv层】
2.4 Computational Complexity and Memory Requirements
深度CNN的复杂性可以分为两部分:
- 卷积层是计算密集型层,包含超过90%的算术运算;
- 全连接层是资源密集处,包含超过 90 90% 90的参数。全连接层是资源密集处,包含超过 90 90% 90的参数。
2.6 Neural Networks With Limited Numerical Precision
Most deep learning frameworks use 32-bit or 64-bit floating point for CNN training and inference.(This paper is to describe the process of quantizing a full precision network to limited precision numbers).
2.6.1 Quantization
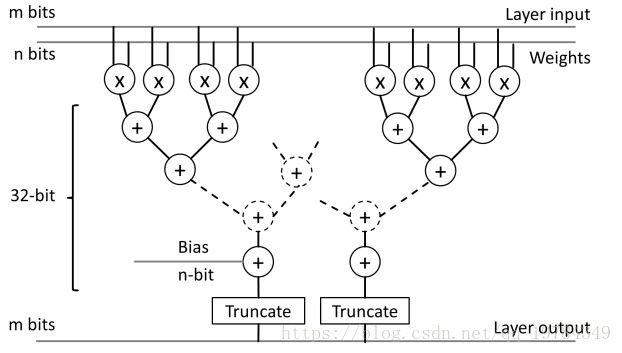
如上图所示,为了简化在硬件上的模拟过程,我们的框架同时量化layer inputs和weights,加法计算使用32-bits的floating point进行计算。加法器在大小和功率上都要比乘法器小。
2.6.2 Rounding Schemes
Round nearest even
r o u n d ( x ) = { ⌊ x ⌋ , i f ⌊ x ⌋ ≤ x ≤ x + ϵ 2 ⌊ x ⌋ + ϵ , i f ⌊ x ⌋ + ϵ 2 < x ≤ x + ϵ round(x) = \begin{cases} \lfloor x \rfloor, & if \ \lfloor x \rfloor \leq x \leq x+\frac{\epsilon}{2} \\ \lfloor x \rfloor + \epsilon , & if \ \lfloor x \rfloor + \frac{\epsilon}{2} < x \leq x + \epsilon \end{cases} round(x)={⌊x⌋,⌊x⌋+ϵ,if ⌊x⌋≤x≤x+2ϵif ⌊x⌋+2ϵ<x≤x+ϵ
Denoting ϵ \epsilon ϵ as the quantization step size and ⌊ x ⌋ \lfloor x \rfloor ⌊x⌋ as the largest quantization value less or equal to x.
As round-nearest-even is deterministic, we chose this rounding scheme for inference
Round stochastic
r o u n d ( x ) = { ⌊ x ⌋ , w . p . 1 − x − ⌊ x ⌋ ϵ ⌊ x ⌋ + ϵ , w . p . x − ⌊ x ⌋ ϵ round(x) = \begin{cases} \lfloor x \rfloor, & w.p. \ 1-\frac{x-\lfloor x \rfloor}{\epsilon} \\ \lfloor x \rfloor + \epsilon , & w.p. \ \frac{x-\lfloor x \rfloor}{\epsilon} \end{cases} round(x)={⌊x⌋,⌊x⌋+ϵ,w.p. 1−ϵx−⌊x⌋w.p. ϵx−⌊x⌋
随机舍入给量化过程增加了随机性,在训练过程可以有一个平均的影响(即平均结果一般为0)。
We chose to use this rounding scheme when quantizing network parameters during fine-tuning.
2.6.3 Optimization in Discrete Parameter Space
在传统的64-bit浮点数训练上,优化问题是在平滑的误差表面上进行。而对于量化网络,误差表面就变成离散的了。
有如下两种方式训练量化网络:
- 从头开始训练量化权重(即没有利用上pre-trained model的权重)
- 在连续领域训练网络,然后量化参数,最后再微调到离散量化空间。
本文更新权重的方式是第二种:: full precision shadow weights. Small weight updates ∆w are applied to the full precision weights w, whereas the discrete weights w1 are sampled from the full precision weights. (在9.3有更多的fine-tune细节而)
3. Related Work
3.1 Network Approximation
3.1.1 Fixed Point Approximation
方法提出的出发点:fixed-point计算比floating point计算需要更少的资源,更快。
所以有一些从fixed-point上工作的方法。比如,在CIFAR-10上工作的16-bit网络;与上一个相同网络架构的7-bit网络;二元/三元网络等。
但这些方法只证明了fixed-point方案能在small Networks上工作良好,但在大网络上效果有限,比如AlexNet。
3.1.2 Network Pruning and Shared Weights
方法提出的出发点:在数据密集型应用的能量耗费上,片外内存(Off-chip)的访问占据了很大一部分。
所以,有一个很重要步骤就是压缩网络的参数数量。Han et al.(2016b)解决了这个问题,其方案分为三个步骤:
- 移除网络中不重要的连接(通过阈值判断)。移除后的稀疏网络经过re-trained后重复进行移除连接;
- 将剩下来的权重进行聚类,从而共享参数 。这些共享的权重也经过re-train以发现optimal centroids;
- 采用零损失压缩方案(比如,Huffman Coding) 压缩最后的权重.
4. Fixed Point Approximation
4.2 Fixed Point Format
fixed point number format: [ I L . F L ] [IL.FL] [IL.FL],其中 I L 和 F L IL和FL IL和FL分别表示整数长度和分数长度。即 b i t w i d t h = I L + F L bit _{width} = IL + FL bitwidth=IL+FL
为了把 floating point 量化成 fixed point,本文使用round-nearest。使用二进制补码数来表示数字,所以最大的正数可以表示为: X m a x = 2 I L − 1 − 2 − F L X_{max}=2^{IL-1}-2^{-FL} Xmax=2IL−1−2−FL
注意,以下的实验中,所有截断的数字都是用共享的固定点格式,即他们共享使用相同的整数和小数长度
4.3 Dynamic Range of Parameters and Layer Outputs
4.3.1 Dynamic Range in Small CNN
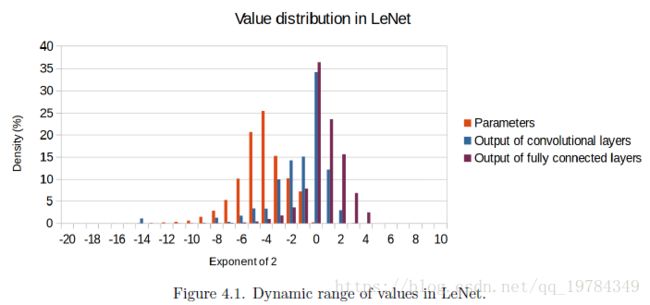
如上图所示,平均而言,参数的大小是要小于layer output的。99%的训练好的网络的参数在 [ 2 0 , 2 10 ] [2^0,2^{10}] [20,210];而对于全连接层, 99 % 99\% 99%的 layer outputs 在 [ 2 − 4 , 2 5 ] [2^{-4},2^5] [2−4,25]。
为了把 layer outputs 和网络参数都量化到 8-bit 的 fixed point,有一部分的参数会饱和(即丢失更多的精度,截断)。作者在 Q . 4.4 Q.4.4 Q.4.4的格式下得到了最高的量化结果,这代表着,相对而言,大的layer output比小的参数要更重要(因为这里 activation 和 weight 都固定到一个格式,其IL 和 FL都是固定的。对activation而言,需要更大的IL;对weight而言,需要更大的FL。这二个结果,代表了结果向IL偏向)。
4.3.1 Dynamic Range in Large CNN

如上图所示,像small networks一样,参数的大小是要小于layer output的,而且这两组数的平均值差距更大了。因为这个动态数值范围比 LeNet更大了,所以需要更多的 bit 来完成 fixed point representations。结果显示,效果最后的是 16-bit 的 fixed point,格式为 Q9.7。可以看出,有相当一部分的参数在这个格式下是饱和的,这意味着小数的Bit长度不足。而只有很少的 layer output( 0.46 % 0.46\% 0.46%的卷积层output)是比这个表示范围大的,而有 21.23 % 21.23\% 21.23%的参数是被截断到 0 0 0的。
这个图的分析结果,和LeNet一样,“大的 layer output 比小的参数更重要”。
5. Dynamic Fixed Point Approximation
从上一章节可以看出,如果 weight 和 layer output使用相同的 fixed point格式,则其中一组数字就会饱和,从而损失精度。所以,本章节介绍了一种 dynamic fixed point,其可以进一步的减小参数size,同时保持高准确率。
5.1 Mixed Precision Fixed Point
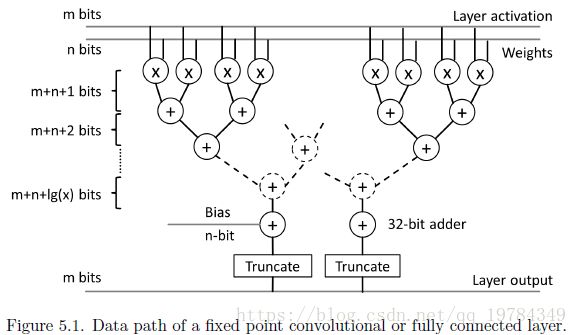
如上图所示,activation 和 weights 分别用 m-bits 和 n-bits表示,在进行了乘法运算后,经过树形加法运算。在每层加法运算进行的同时,用 +1 bit 的空间来存储,以避免溢出。最后一层加法,用 m + n + l g ( x ) m+n+lg(x) m+n+lg(x) bits存储,其中,x为乘法运算的个数。
5.2 Dynamic Fixed Point
Dynamic Fixed Point是为了解决Fixed Point表达能力受限的问题,Dynamic Fixed Point固定的是bit-width,而FL由 value group决定,对于每一层的每一个type的数值,都有一个常数FL(即其IL和FL是确定的)。
在Dynamic Fixed Point中,每个数字都可以表达为如下形式: ( − 1 ) s 2 − F L ∑ i = 0 B − 2 2 i x i (-1)^{s}2^{-FL}\sum_{i=0}^{B-2}2^ix_i (−1)s2−FLi=0∑B−22ixi
Choice of Number Format
在每一层的每一个Type的数值而言,其Fixed Point的格式为: I L = ⌈ l g 2 ( m a x ( x ) ) + 1 ⌉ IL=\lceil lg_2(max(x))+1\rceil IL=⌈lg2(max(x))+1⌉ 即保证IL足够让所有的数都包括进来,而不向上饱和。
注意,这种计算 IL 的方法,适用于 layer parameters;对于 layer outputs,用这个公式 减去 1 来表达 IL。
可以看出,即使是已经压缩过的模型,如 SqueezeNet 都能在 ImageNet 上以 8-bit 达到很好的结果。
8. Comparison of Different Approximations
对于硬件加速器来说,Fixed Point Approximation 是耗时和耗能量最少的。但是,当bit变小时,Fixed Point也是表现最差的。(会向上饱和)
对比minifloat和Fixed Point,Dynamic Fixed Point是三种近似方案中最好的。动态固定点使其能覆盖很大的动态范围(动态固定点隐式存储: I L = ⌈ l g 2 ( m a x ( x ) ) + 1 ⌉ IL=\lceil lg_2(max(x))+1\rceil IL=⌈lg2(max(x))+1⌉)。
9. Ristretto: An Approximation Framework for Deep CNNs
9.2 Quantization Flow

Ristretto 将网络模型从 32-bit floating 量化到 fixed point,有如上图的五个阶段:
- 统计、分析Weight信息, 分配足够的bit给实数部分;(大的数比较重要)
- 前向传播成千上万的图片,统计、分析Activation信息,分配足够的bit给实数部分;
- 给每一种类型的array决定bit分配,用二分查找法寻找最优的bit;(应该是分别对conv weight、fc weight、layer output分别决定一个bit分配,即所有的相同类型层共用一个格式)
- 评估每种bit的分配带来的误差;(在二分查找一个类型的最优bit时,其余两种类型保留floating point形式)
- 找到每个部分的最优bit后,开始fine-tune
9.3 Fine-tuning
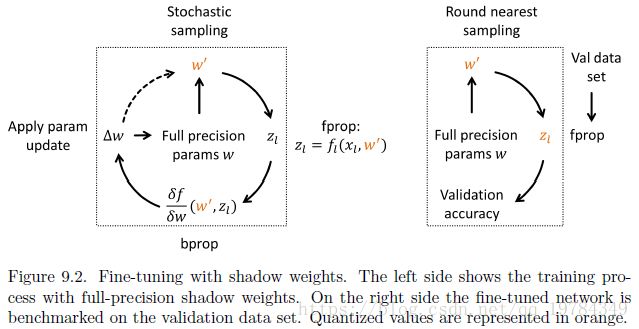
Fine-Tuning步骤如上图所示:
注意,activation在Fine-Tuning步骤不进行量化;
- 利用量化后的离散值 w ′ w' w′ 进行前向传播计算activation/output;
- 利用量化后的离散值 w ′ w' w′ 进行反向传播传播计算gradient;
- 将gradient应用在floating point的w上进行参数更新(防止更新的范围 △w不足step-size)
在预测阶段,activation才进行量化。
在微调阶段,为了充分利用per-trained的参数信息,使用的学习率比上一次全精度训练迭代低一个数量级。
9.5 Ristretto From a User Perspective