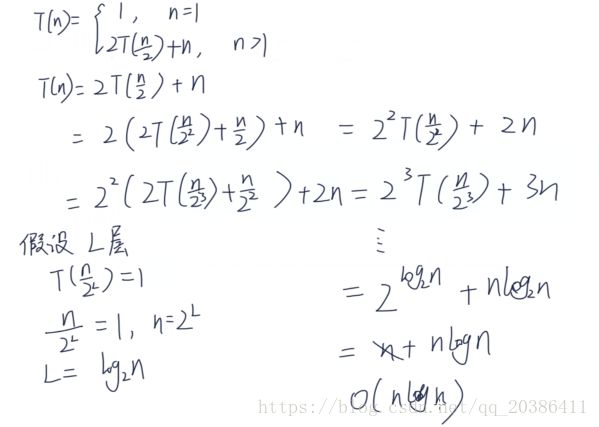数据结构——排序和查找

递归时间复杂度的计算：

知道一般递归的时间复杂度为O(nlogn)

写递归方法时一定要注意出口条件，否则会一直递归下去

 

排序

1、快速排序：最好的排序算法，递归实现

选用数组的第一个数，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面（一趟排序）

交换ki和kj

 

①找中间值，数据分为两部分

②小于中间值数据放左边，大于中间值数据放右边，再用步骤①处理左右两边数据

具体步骤：

1、取第一个数为k，从左向右找大数kj，从右向左找小数ki

若大数位置在小数前面，交换ki和kj位置，继续1步骤

若大数位置在小数后面，交换kj和基数位置，然后继续1步骤

时间复杂度：

一趟排序后，有一个元素被放在正确的位置上

不是稳定排序法（时间复杂度没有弄明白？）：

在最差情况下，划分之后一边是一个，一边是n-1个。划分由 n 个元素构成的数组需要进行 n 次比较（每次交换大数和小数后重新开始遍历数组）和 n 次移动。因此划分所需时间为 O(n)  。该算法需要 (n-1)+(n-2)+…+2+1= O(n^2) 时间。

在最佳情况下，每次主元将数组划分为规模大致相等的两部分。设 T(n) 表示使用快速排序算法对包含 n 个元素的数组排序所需的时间，因此，和归并排序的分析相似，快速排序的 T(n)= O(nlogn)。（递归的时间复杂度）

程序实现：

①比较暴力的方法：递归实现，左边部分+第一个元素+右边部分

def quicksort(lis):
    if len(lis)<2:
        return lis#只有一个元素时，直接返回该元素
    else:
        base=lis[0]#设置第一个元素为比较元素，即基元素
        left_part = [i for i in lis[1:] if i < base]  # 这里的索引值必须从1开始
        right_part = [j for j in lis[1:] if j >= base]
        '''
        left_part=[i for i  in range(1,len(lis)) if i=base]
                '''
    return quicksort(left_part)+[base]+quicksort(right_part)

lis=[3,6,2,9,8]
print(quicksort(lis))

这个错误之前肯定犯过很多次，列表在不需要索引的情况下可以用lis[0:]来进行遍历

这个算法暴力在增加了空间复杂度，每次的left_part和right_part都需要空间来存储

②改进方法：对应上面的解释过程（视频讲解程序没有实现出来）

不使用中间变量怎么交换数据

lis=1
base=2
# base,lis=lis,base#一行写是交换数据，输出结果为2 1
base=lis#两行写是赋值，最后输出结果为1 1
lis=base
print(lis,base)

 

2、冒泡排序（相邻交换，一次扫描完后，最后一个值一定是最大的）

两元素窗口不断向后移动，窗口中前面元素大于后面元素则交换元素位置。窗口走第一趟，最右边的元素变为最大，窗口走第二趟只需要走到倒数第二个元素，则倒数第二个元素变为最大

核心：比较元素大小

时间复杂度：

最坏情况：按照从大到到小的顺序排列，第一趟比较n-1次（交换n-1次），第二趟比较n-2次……(n-1)+(n-2)+……+2+1=n(n-1)/2，所以时间复杂度为O(n^2)

最好情况：当数据本来就排序好，走一趟不需要数据交换时，只需要比较n-1即可，时间复杂度为O(n)

程序实现：

def bubbleSort(nums):
    for i in range(len(nums)-1):    # 这个循环负责设置冒泡排序进行的次数
        for j in range(len(nums)-i-1):  # 每次扫描完，下一次扫描比较的次数会少一次，所以需要减去i
            if nums[j] > nums[j+1]:
                nums[j], nums[j+1] = nums[j+1], nums[j]
    return nums

nums = [5,2,45,6,8,2,1]

print(bubbleSort(nums))

为什么当时自己脑子一片空白，原因：自己随便写一个列表出来啊！

 

 

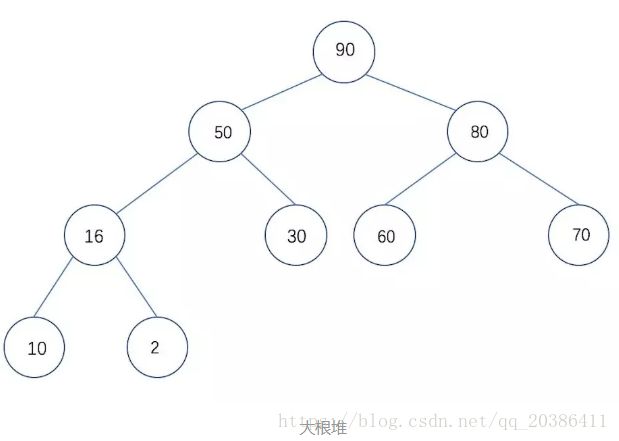
3、堆排（堆积排序，堆是一种完全二叉树）看不懂？

在这里要注意区分堆和堆栈，堆表示二叉树

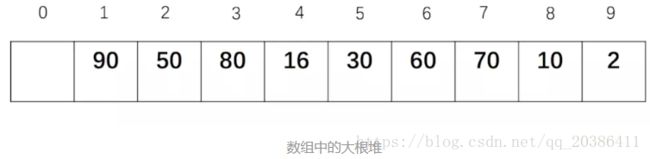
用数组实现堆，没有用到二叉树

如何将一个列表构造成大根堆：

拿到一个列表，肯定是乱序的。现在需要比较节点值，调整元素位置。一个for循环就可以将列表顺序调整为大根堆的顺序（这个顺序在堆中是从大到小的，但是在列表中不是）

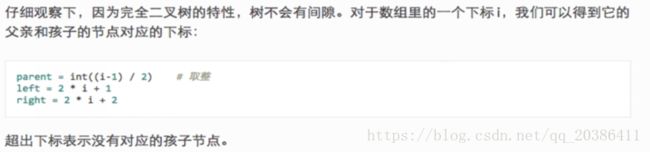
需要将堆顶元素取出后，继续将列表转为大根堆

 

有孩子的最大索引值为len(lis)//2

https://www.jianshu.com/p/d174f1862601详细链接

 

选择排序（找最小值交换）:依次选出最小值放在最前面

时间复杂度：因为需要找最小/大值，因此需要比较次数(n-1)+(n-2)+……+2+1=n(n-1)/2，所以时间复杂度为O(n^2)

比如有7个元素

for i in range(7):

   for j in range(i+1,8):

        if data[i]>data[j]

            data[i]=data[j]

            data[j]=data[i]

堆排是选择排序的改进版，减少选择排序中的比较次数

堆排用堆积树完成排序的，堆积树的节点值大于左右子节点值，根节点值最大（分为最小堆和最大堆，最小堆的根节点值最小）

数组二叉树（每层从左往右写的顺序将数组转化为二叉树）转化为堆积树：

每一层之间的值不比较，而是层与上一层值比较，若子节点值比节点值大，交换位置，再将交换位置的值与上上层的节点值比较，直到与根节点值比较为止

时间复杂度O(nlogn)

最快的平均比较次数为nlogn，nlogn的曲线图介于n^2和n之间

 

归并排序：while循环

两个有序数组使归并结果元素从小到大排序（注意两个数组已经是有序的）

lis_a=[1,3,5,7]
lis_b=[2,4,6,8,9,10]
a,b=len(lis_a),len(lis_b)

#给两个指针（视频中是这样解释的，新的理解：赋值的变量可以当做指针）
i=j=0
lis=[]

while i

只需要比较a或b次（比较次数为列表长度较短的值），即O(n)

 

其他排序（了解过程）

插入排序：将数组的前两个元素先排好，再将第三个元素插入适当的位置，再继续将后面的元素插入适当位置

显然最差情况O(n^2)，最好情况是从大到小的列表时间复杂度为O(n)

 

 

查找（查找数组中是否有某一个元素）

顺序查找：

最后一个元素才是要找的数据，即最差情况需要比较n次，时间复杂度为O(n)

怎么不用排序的方法找出中位数（之前和彭讨论就是说的此方法，还是用的排序的方法）

 

算法稳定与否：

排序后两个键值保持原来的相对前后次序

排序后7左任然在7右的左边则是稳定的排序

 

哈希查找：通俗理解就是存在索引值

更具数据可以建立哈希表

 

哈希查找的应用：无序数组中找出和为N的两个数（三个数、四个数）

两个数：

统一用此方法

def getRes_HashMap(nums, target):
    result = []
    for i in range(0,len(nums)-1):#i只能取到最后一个数的前一个数
        if (target - nums[i]) in nums[i + 1:]:
            result.append((nums[i], target - nums[i]))
    return result

三个数和：

第一个指针轮询列表

第二个指针轮询第一个指针后面的列表

判断第三个值是否在第二个指针后面的列表

def Sum3(arr, target):  # 3sum问题
    res = []
    for i in range(0,len(arr)-2):#
        for j in range(i+1,len(arr)-1):
            if(target-arr[i]-arr[j]) in arr[j+1:]:
                res.append((arr[i],arr[j],target-arr[i]-arr[j]))
    print(res)

'''
#去重操作
def Sum3(arr, target):  # 3sum问题
    res = []
    for i in range(0,len(arr)-2):#
        for j in range(i+1,len(arr)-1):
            if(target-arr[i]-arr[j]) in arr[j+1:]:
                temp=[arr[i],arr[j],target-arr[i]-arr[j]]
                temp.sort()
                res.append(tuple(temp))                
    print(list(set(res)))
'''
if __name__ == '__main__':
    arr = [int(i) for i in input().split()]
    target = int(input())
    Sum3(arr, target)

注;

这里有一种特殊情况没有考虑，可能出现重复的情况

-1 0 1 2  -1 -4
0
[(-1, 0, 1), (-1, 2, -1), (0, 1, -1)]所以要进行去重

四个和：三层for循环

def Sum3(arr, target):  # 4sum问题
    res = []
    for i in range(0,len(arr)-3):#4sum问题，是减3，不是减4，索引错了结果肯定是错的
        for j in range(i+1,len(arr)-2):
            for k in range(j+1,len(arr)-1):
                if(target-arr[i]-arr[j]-arr[k]) in arr[k+1:]:
                    temp=[arr[i],arr[j],arr[k],target-arr[i]-arr[j]-arr[k]]
                    temp.sort()
                    res.append(tuple(temp))
    print(list(set(res)))

if __name__ == '__main__':
    arr = [int(i) for i in input().split()]
    target = int(input())
    Sum4(arr, target)

别人面试问到:不使用排序的方法怎么找到一个数组的中位数