openpose实验总结

六种人体姿态估计的深度学习模型和代码,详情可参考链接
四款人体姿势关键点估计论文链接

openpose下载可参考链接安装与调试可参考链接（亲测有效）
这里整理一下论文Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields的原理。

Introduction

论文首先指出了Pose Estimation的三个关键性挑战：首先，每一个的图像可能包含未知数量的人，他们可能出现在图像的任何位置，大小也不一定；其次，例如相互接触、遮挡等都使得对关键点的关联更加困难。还有，随着图像中人的数量增加，程序的运行时间复杂度也会上升，这使得实时监测的表现成为一个挑战。然后论文中指出了现有的一些方法存在的问题：现有的一些方法主要由person detector和single-person pose estimation两部分组成，就是给定一张图片，先做人体的检测，在每个人的位置上都得到一个边缘方框信息，在每个方框上，做单人的人体姿态估计，重复这个步骤，直到得到最终的结果。这些top-down的方法在性能上很依赖于人体姿态检测的结果，如果person detector检测失败了（当多个人挨得很近的时候），这些方法可能就不奏效了。另外一个就是时间的问题，算法速度与图片上人的数目成正比，假如说一张图有30个人，它要重复30次单人的人体估计，这样使得这个方法在复杂场景下变得十分缓慢。

Method

文章的核心是提出一种利用Part Affinity Fields（PAFs）的自下而上的人体姿态估计算法。研究自下而上算法（得到关键点位置再获得骨架）而不是自上而下算法（先检测人，再回归关键点）。首先检测人关键点的位置，比如图片上人体右肩膀的位置，得到检测结果是通过预测人体关键点的热点图，可以看到在每个人体关键点上都有一个高斯的峰值，代表神经网络相信这里有一个人体的关键点。同样的我们对其他人体关键点比如说右手肘作同样的处理，得到这个检测结果。在得到检测结果之后，对关键点检测结果进行连接，换句话说，就是想知道每个关键点具体是属于图片中哪个人。
对于这个步骤，他们的方法是通过一个新的特征进行推测，这个特征是一个矢量场，叫作人体关键点亲和场（PAFs），在后面会具体介绍这个特征的表示，这里先整体介绍方法的结构。然后重复这个步骤，对另外关键点之间（另外人体的躯干）的连接进行推测，同样是通过人体关键点亲和场来进行推测，重复这个步骤，直到得到人体的全部骨架信息。
执行过程如下图所示，一张输入图像w*h，然后模型同时得到人体部位位置的confidence maps集合S和一个用来说明关节点关联的part affinities集合L。得到一张图像中所有人的2D关键点，他们的创新点就是设计了一个设计了一个深度学习网络结构，同时学习人体关键点的检测和人体关键点的连接。并且，同时学习会使得他们互相帮助，得到更好的结果。

Simultaneous Detection and Association

PAFs是用来描述像素点在骨架中的走向，用L(p)表示；关键点的响应用S(p)表示。先看主体网络结构，图像首先被一个卷积神经网络处理后生成特征图集F（通过VGG-19的前10层进行初始化并微调）网络采用VGG pre-train network作为骨架，有两个分支分别回归L(p)和S(p)。每一个stage算一次loss，之后把L和S以及原始输入concatenate，继续下一个stage的训练。随着迭代次数的增加，S能够一定程度上区分结构的左右。loss用的L2范数，S和L的ground-truth需要从标注的关键点生成，如果某个关键点在标注中有缺失则不计算该点。记为F，经过如图所示的网络，该网络分上下两个分支，每个分支都有t个阶段（表示越来越精细），每个阶段都会将feature maps进行融合。其中ρ φ 表示网络。

Confidence Maps for Part Detection

下边给出根据标注数据计算groundtruth confidence maps S∗的方法，每个confidence map都是一个2D表示。理想情况下，当图像中只包含一个人时，如果一个关键点是可见的话对应的confidence map中只有一个峰值；当图像中有多个人时，对于每一个人k的每一个可见关键点j在对应的confidence map中都会有一个峰值。首先给出每一个人k的单个confidence maps， xj,k∈ℝ2 x j , k ∈ R 2 表示图像中人k对应的位置j对应的groundtruth position，数值如公式(6)所示，其中σ用来控制峰值在confidence map中的传播范围。对应多个人的confidence map见公式(7)，这里用最大值而不是平均值能够更准确地将同一个confidence map中的峰值保存下来。
S∗j,k(p)=exp(−|p−xj,k|22σ2),(6) S j , k ∗ ( p ) = e x p ( − | p − x j , k | 2 2 σ 2 ) , ( 6 )
S∗j(p)=maxkS∗j,k(p),(7) S j ∗ ( p ) = max k S j , k ∗ ( p ) , ( 7 )

Part Affinity Fields for Part Association

给定一组关键点，如Figure 5(a)所示，我们如何把它们组装成未知数量的人的整个身体的pose呢？我们需要一个置信方法来确定每队关键点之间的连接，即它们属于同一个人。一个可能的方法是找到一个位于每一对关键点之间的一个中间点，后检查中间点是真正的中间点的概率，如Figure 5(b)所示。但是当人们挤在一块儿的时候，通过这样的中间点可能得出错误的连接线，如Figure 5(b)中绿线所示。出现这种情况的原因有两个：(1)这种方式只编码了位置信息，而没有方向；(2)躯体的支撑区域已经缩小到一个点上。为了解决这些限制，我们提出了称为part affinity fields的特征表示来保存躯体的支撑区域的位置信息和方向信息，如Figure 5(c)所示。对于每一条躯干来说，the part affinity是一个2D的向量区域。在属于一个躯干上的每一个像素都对应一个2D的向量，这个向量表示躯干上从一个关键点到另一个关键点的方向。特别的，对两个候选部分位置我们沿着线段对预测部分亲和域Lc进行取样，来测量它们联系的置信度。

考虑下图中给出的一个躯干（手臂），令 Xj1,k X j 1 , k 和 xj2,k x j 2 , k 表示图中的某个人k的两个关键点 j1 j 1 和 j2 j 2 对应的真实像素点，如果一个像素点p位于这个躯干上，值 L∗c,k(p) L c , k ∗ ( p ) 表示一个从关键点 j1 j 1 到关键点 j2 j 2 的单位向量，对于不在躯干上的像素点对应的向量则是零向量。下面这个公式给出了the groundtruth part affinity vector，对于图像中的一个点p其值 L∗c,k(p) L c , k ∗ ( p ) 的值如下：


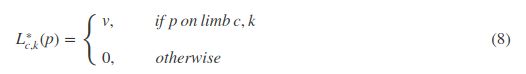
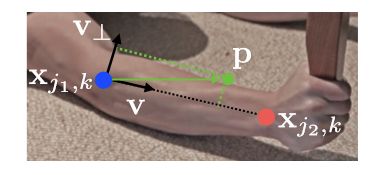
其中， v=(xj2,k−xj1,k)/|xj2,k−xj1,k|2 v = ( x j 2 , k − x j 1 , k ) / | x j 2 , k − x j 1 , k | 2 表示这个躯干对应的单位方向向量。属于这个躯干上的像素点满足下面的不等式，其中 σl σ l 表示像素点之间的距离，躯干长度为 lc,k=|xj2,k−xj1,k|2 l c , k = | x j 2 , k − x j 1 , k | 2 ， v⊥ v ⊥ 表示垂直于v的向量。

0≤v⋅(p−xj1,k)≤lc,kand|v⊥⋅(p−xj1,k)|≤σl 0 ≤ v ⋅ ( p − x j 1 , k ) ≤ l c , k a n d | v ⊥ ⋅ ( p − x j 1 , k ) | ≤ σ l

整张图像的the groundtruth part affinity field取图像中所有人对应的affinity field的平均值，其中 nc(p) n c ( p ) 是图像中k个人在像素点p对应的非零向量的个数。

L∗c(p)=1nc(p)∑kL∗c,k(p)(9) L c ∗ ( p ) = 1 n c ( p ) ∑ k L c , k ∗ ( p ) ( 9 )

在预测的时候，我们用候选关键点对之间的PAF来衡量这个关键点对是不是属于同一个人。具体地，对于两个候选关键点对应的像素点 dj1 d j 1 和 dj2 d j 2 ，我们去计算这个PAF，如下式所示。

E=∫u=1u=0Lc(p(u))⋅dj2−dj1|dj2−dj1|2du(10) E = ∫ u = 0 u = 1 L c ( p ( u ) ) ⋅ d j 2 − d j 1 | d j 2 − d j 1 | 2 d u ( 10 )

其中，p(u)表示两个像素点 dj1 d j 1 和 dj2 d j 2 之间的像素点：

p(u)=(1−u)dj1+udj2(11) p ( u ) = ( 1 − u ) d j 1 + u d j 2 ( 11 )

MultiPerson Parsing using PAFs

借助非最大抑制，我们从预测出的confidence maps得到一组离散的关键点候选位置。因为图像中可能有多个人或者存在false positive，每个关键点可能会有多个候选位置，因此也就组成了很大数量的关键点对，如Figure 6(b)所示。按照公式(10)，我们给每一个候选关键点对计算一个分数。从这些关键点对中找到最优结果，是一个NP-Hard问题。下面给出本文的方法。

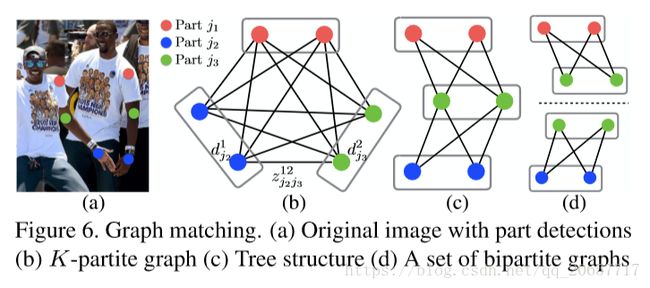
假定模型得到的所有候选关键点构成集合 DJ={dmj:forj∈{1...J},m∈{1...Nj}} D J = { d j m : f o r j ∈ { 1... J } , m ∈ { 1... N j } } ，其中 Nj N j 表示关键点j的候选位置数量， dmj∈ℝ2 d j m ∈ R 2 是关键点j的第m个候选位置的像素坐标。我们需要做的是将属于同一个人的关键点连成躯干（胳膊，腿等），为此我们定义变量 zmnj1j11∈{0,1} z j 1 j 1 1 m n ∈ { 0 , 1 } 表示候选关键
dmj1 d j 1 m 和 dmj2 d j 2 m 是否可以连起来。如此以来便得到了集合 Z={zmnj1j2:forj1,j2∈{1...J},m∈{1...Nj1},n∈{1...Nj2}} Z = { z j 1 j 2 m n : f o r j 1 , j 2 ∈ { 1... J } , m ∈ { 1... N j 1 } , n ∈ { 1... N j 2 } } 。现在单独考虑第c个躯干如脖子，其对应的两个关键点应该是 j1 j 1 和 j2 j 2 ，这两个关键点对应的候选集合分别是 Dj1 D j 1 和 Dj2 D j 2 ，我们的目标如下所示。

maxZcEc=maxZc∑m∈Dj1∑n∈Dj2Emn⋅zmnj1j2,(12) max Z c E c = max Z c ∑ m ∈ D j 1 ∑ n ∈ D j 2 E m n ⋅ z j 1 j 2 m n , ( 12 )
s.t.∀m∈Dj1,∑n∈Dj2zmnj1j2≤1,(13) s . t . ∀ m ∈ D j 1 , ∑ n ∈ D j 2 z j 1 j 2 m n ≤ 1 , ( 13 )
∀n∈Dj2,∑m∈Dj1zmnj1j2≤1,(14) ∀ n ∈ D j 2 , ∑ m ∈ D j 1 z j 1 j 2 m n ≤ 1 , ( 14 )
其中， Ec E c 表示躯干c对应的权值总和， Zc Z c 是躯干c对应的Z的子集， Emn E m n 是关键点 dmj1 d j 1 m 和 dmj2 d j 2 m 对应的part affinity，公式(13)和公式(14)限制了任意两个相同类型的躯干（例如两个脖子）不会共享关键点。问题扩展到所有C个躯干上，我们优化目标就变成了公式(15)。

maxZE=∑Cc=1maxZcEc,(15) max Z E = ∑ c = 1 C max Z c E c , ( 15 )

Results

至此，整个模型就说完了，下面是模型在COCO 2016和MPII两个数据集上多的结果。在预测的时候，论文中使用了同一张图像的3个尺寸(×0.7,×\1,×1.3)输入进去来得到比单个尺寸更好的结果。


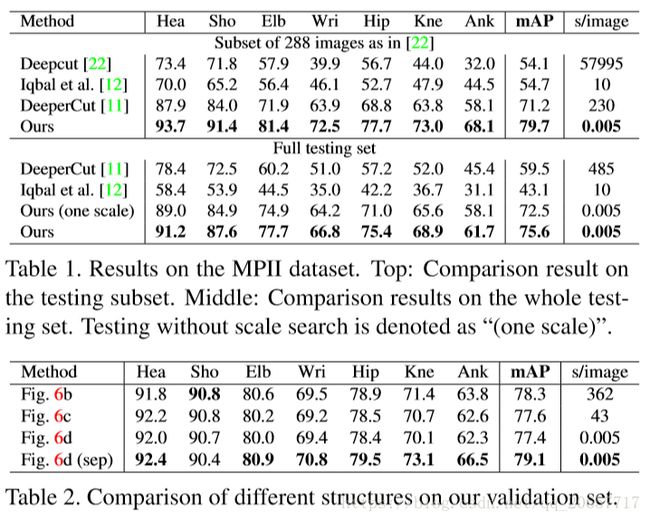
参考自博客：https://blog.csdn.net/MajorDong100/article/details/78944982