MATLAB 常微分方程数值解法--中心差分法、向前差分、向后差分
这道题就是一个引子,可能其他专业同学,对这种问题不甚了解。不过没有关系,丝毫不影响我们今天进行内容的分析。
题目二:(微分方程边值问题)梁挠度方程数值求解已知: 设一跟长为 L 的矩形截面的梁,两端固定。E 是弹性模量,S 是端点作用力,I(x)是惯性矩,q 是均匀荷载强度,梁的桡度 y(x)满足如下方程,梁及荷载请自行设计。
要求:(1)分别用向前差分、向后差分及中心差分方法。
这里,我假设 q=1kN/m ,l=5m,b=300mm,h=180mm,E=10Gpa,S=5kN.经过一系列的带入上面表达式和进行单位的统一计算我们可以得到下面的式子。
![]()
之后的程序都是围绕着这个方程,和两个边界条件进行的。
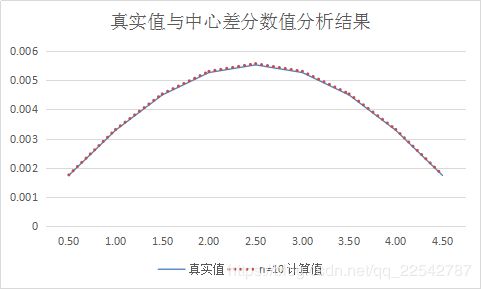
下面是中心差分的matlab程序
function [A,b,U,D,L,x]= zhongxincafen(a,b,n)
%输入时:主意 阿尔法和贝塔的值是要变化的 y''+p(x)*y'+q(x)*y=f(x)
% a 是初始值 y(a)=阿尔法,b是最终值 y(b)=贝塔 ,n是分段数
format long
h = 0.5;% 有些时候 需要输入 例如 等于 0
disp(h);
A=zeros(n-1,n-1);
b=zeros(n-1,1);
syms x
q =[];
p=[];
r=[];
for i =1 :n-1
x=0+i*h;
p(i)=0; % 变化 请更改成为 x 的函数 例子 :p(i) =-x/(1+x^2)
q(i) =(-5/1458); % 变化 请更改成为 x 的函数
r(i)=(x^2-5*x)/(2916); % 变化 请更改成为 x 的函数
if i == 1
A(1,1)=-2 + h^2 * q(i);
A(1,2)= 1 + 0.5 * h * p(i);
b(1,1)=h^2* r(i)-(1-0.5*h*p(i))*0; % 初值的阿尔法
elseif i<=n-2
A(i,i-1)=1-0.5*h*p(i);
A(i,i)=-2+h^2*q(i);
A(i,i+1)=1+0.5* h *p(i);
b(i,1)=h^2 *r(i);
elseif i == n-1
A(i,i-1)=1-0.5*h*p(i);
A(i,i)=-2+h^2*q(i);
b(i,1)=h^2 *r(i)-(1+0.5 * h * p(i))*0 %贝塔
end
D =zeros(1,n-1);
L =zeros(1,n-1);
U =zeros(1,n-1);
D =diag(A)';
L =diag(A,-1)';
U =diag(A,1)';
U(1,n-1)=0;
for tu=n:-1:3
L(1,tu-1)= L(1, tu-2);
end
L(1,1)=0;
x = threedia (L,D,U,b);
end
function x = threedia (a,b,c,f)
N= length(f);
x = zeros (1,N);y = zeros(1,N);
d = zeros(1,N);u = zeros(1,N);
d(1)=b(1);
for i =1 :N -1
u(i)=c(i)/d(i);
d(i+1)=b(i+1)-a(i+1)*u(i);
end
%过程
y(1)=f(1)/d(1);
for i= 2 :N
y(i)=( f(i)-a(i)*y(i-1))/d(i);
end
%赶的过程
x(N)=y(N);
for i = N-1:-1:1
x(i)=y(i)-u(i)*x(i+1);
end
x=x'
clear all
a=0;b=0;n =10
[A,b,U,D,L,x]= zhongxincafen(a,b,n)
向后和向前差分法,只给出程序 见https://download.csdn.net/download/qq_22542787/10795173 和 https://download.csdn.net/download/qq_22542787/10795178