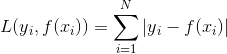GBDT基本原理及算法描述

一. 前言

在AdaBoost基本原理与算法描述中，我们介绍了AdaBoost的基本原理，本篇博客将介绍boosting系列算法中的另一个代表算法GBDT（Gradient Boosting Decision Tree，梯度提升树）算法。这里对GBDT的学习做一个总结，也希望对有帮助的同学能有一个帮助。

在介绍AdaBoost的时候我们讲到了，AdaBoost算法是模型为加法模型，损失函数为指数函数，学习算法为前向分步算法时的分类问题。而GBDT算法是模型为加法模型，学习算法为前向分步算法，基函数为CART树，损失函数为平方损失函数的回归问题，为指数函数的分类问题和为一般损失函数的一般决策问题。在针对基学习器的不足上，AdaBoost算法是通过提升错分数据点的权重来定位模型的不足，而梯度提升算法是通过算梯度来定位模型的不足。

当GBDT的损失函数是平方损失时，即时，则负梯度，而即为我们所说的残差，而我们的GBDT的思想就是在每次迭代中拟合残差来学习一个弱学习器。而残差的方向即为我们全局最优的方向。但是当损失函数不为平方损失时，我们该如何拟合弱学习器呢？大牛Friedman提出使用损失函数负梯度的方向代替残差方向，我们称损失函数负梯度为伪残差。而伪残差的方向即为我们局部最优的方向。所以在GBDT中，当损失函数不为平方损失时，用每次迭代的局部最优方向代替全局最优方向（这种方法是不是很熟悉？）。

说了这么多，现在举个例子来看看GBDT是如何拟合残差来学习弱学习器的。我们可以证明，当损失函数为平方损失时，叶节点中使平方损失误差达到最小值的是叶节点中所有值的均值；而当损失函数为绝对值损失时，叶节点中使绝对损失误差达到最小值的是叶节点中所有值的中位数。相关证明将在最后的附录中给出。

训练集是4个人，A，B，C，D年龄分别是14，16，24，26。样本中有购物金额、上网时长、经常到百度知道提问等特征。提升树的过程如下：（图片来源）

从上图可以看出，第一棵树建立的时候使用的是原始数据，而后每一棵树建立使用的是前n-1次的残差来拟合弱学习器。

下面，我们就来简单的介绍一下GBDT的基本原理和算法描述。

二. GBDT回归树基本模版

梯度提升算法的回归树基本模版，如下所示：

输入：训练数据集，损失函数为

输出：回归树

（1）初始化：（估计使损失函数极小化的常数值，它是只有一个根节点的树，一般平方损失函数为节点的均值，而绝对损失函数为节点样本的中位数）

                       

（2）对（M表示迭代次数，即生成的弱学习器个数）：

（a）对样本，计算损失函数的负梯度在当前模型的值将它作为残差的估计，对于平方损失函数为，它就是通常所说的残差；而对于一般损失函数，它就是残差的近似值（伪残差）：

                      

（b）对拟合一个回归树，得到第m棵树的叶节点区域，（J表示每棵树的叶节点个数）

（c）对，利用线性搜索，估计叶节点区域的值，使损失函数最小化，计算

                    

（d）更新

                    

（3）得到最终的回归树

                               

三. GBDT的算法描述

3.1 GBDT的损失函数

在sklearn中梯度提升回归树有四种可选的损失函数，分别为'ls：平方损失'，'lad:绝对损失'，'huber：huber损失'，'quantile：分位数损失'；而在sklearn中梯度提升分类树有两种可选的损失函数，一种是‘exponential：指数损失’，一种是‘deviance：对数损失’。下面分别介绍这几种损失函数。

3.1.1 梯度提升回归树损失函数介绍

（1）ls：平方损失，这是最常见的回归损失函数了，如下：

                  

（2）lad：绝对损失，这个损失函数也很常见，如下：

                             

对应负梯度为：

                             

（3）huber：huber损失，它是平方损失和绝对损失的这种产物，对于远离中心的异常点采用绝对损失，而中心附近的点采用平方损失。这个界限一般用分位数点度量。损失函数如下：

                            

对应的负梯度为：

                            

（4）quantile：分位数损失，它对应的是分位数回归的损失函数，表达式如下：

                           

其中θ为分位数，需要我们在回归前指定。对应的负梯度为：

                          

对于huber损失和分位数损失主要作用就是减少异常点对损失函数的影响。

3.1.2 梯度提升分类树损失函数介绍

（1）exponential：指数损失，表达式如下：

                          

（2）deviance：对数损失，类似于logistic回归的损失函数，输出的是类别的概率，表达式如下：

                          

下面我们来分别的介绍一下，这几种损失函数对应GBDT算法。

3.2 GBDT回归算法描述

3.2.1 平方损失GBDT算法描述

输入：训练数据集，损失函数为

输出：回归树

（1）初始化：（可以证明当损失函数为平方损失时，节点的平均值即为该节点中使损失函数达到最小值的最优预测值,证明在最下面的附录给出）

                         

（2）对：

（a）对样本，计算伪残差（对于平方损失来说，伪残差就是真残差）

                      ，

（b）对拟合一个回归树，得到第m棵树的叶节点区域，

（c）对，利用线性搜索，估计叶节点区域的值，使损失函数最小化，计算

                    ，K表示第m棵树的第j个节点中的样本数量

上式表示的取值为第m棵树的第j个叶节点中伪残差的平均数

（d）更新

                    

（3）得到最终的回归树

                               

3.2.2 绝对损失GBDT算法描述

输入：训练数据集，损失函数为

输出：回归树

（1）初始化：（可以证明当损失函数为绝对损失时，节点中样本的中位数即为该节点中使损失函数达到最小值的最优预测值,证明在最下面的附录给出）

                       

（2）对：

（a）对样本，计算伪残差

                      ，

（b）对拟合一个回归树，得到第m棵树的叶节点区域，

（c）对，，计算

                    

上式表示的取值为第m棵树的第j个叶节点中伪残差的中位数

（d）更新

                    

（3）得到最终的回归树

                               

3.2.3 huber损失GBDT算法描述

输入：训练数据集，损失函数为

输出：回归树

（1）初始化：

                       

（2）对：

（a）对样本，计算

                      

表示分位数；表示将伪残差的百分之多少设为分位数，在sklearn中是需要我们自己设置的，默认为0.9

                      

（b）对拟合一个回归树，得到第m棵树的叶节点区域，

（c）对，，计算

                    

                    

（d）更新

                    

（3）得到最终的回归树

                               

3.3 GBDT分类算法描述

GBDT分类算法思想上和GBDT的回归算法没有什么区别，但是由于样本输出不是连续值，而是离散类别，导致我们无法直接从输出类别去拟合类别输出误差。为了解决这个问题，主要有两种方法。一是用指数损失函数，此时GBDT算法退化为AdaBoost算法。另一种方法是用类似于逻辑回归的对数似然损失函数的方法。也就是说，我们用的是类别的预测概率值和真实概率值的差来拟合损失。当损失函数为指数函数时，类似于AdaBoost算法，这里不做介绍，下面介绍损失函数为log函数时的GBDT二分类和多分类算法。

3.3.1 log损失GBDT的二分类算法描述

输入：训练数据集，损失函数为，y={-1，1}

输出：分类树

（1）初始化：

                       

（2）对：

（a）对样本，计算伪残差

                      

（b）对概率残差拟合一个分类树，得到第m棵树的叶节点区域，

（c）对，，计算

                    

（d）更新

                    

（3）得到最终的分类树

                               

由于我们用的是类别的预测概率值和真实概率值的差来拟合损失，所以最后还要讲概率转换为类别，如下：

                               

                               

最终输出比较类别概率大小，概率大的就预测为该类别。

3.3.2 log损失GBDT的多分类算法描述         

输入：训练数据集，损失函数为，=｛0，1｝表示是否属于第k类别，1表示是，0表示否。，表示共有多少分类的类别。

输出：分类树

（1）初始化：

                       ，

（2）对：

（a）计算样本点俗属于每个类别的概率：

                    

（b）对k=1,2,...,K：

        1） ，

        2）对概率伪残差拟合一个分类树

        3）

        4）

（3）得到最终的分类树

                               

最后得到的可以被用来去得到分为第k类的相应的概率：

                               

由于我们用的是类别的预测概率值和真实概率值的差来拟合损失，所以最后还要将概率转换为类别，如下：

                               

为最终的输出类别，为当真实值为时，预测为第k类时的联合代价，即概率最大的类别即为我们所预测的类别。当K=2时，该算法等价于为二分类算法。

到这里，我们算法的描述环节已经介绍完毕。还有一个算法就是分位数回归的算法描述没有介绍，因为早期的论文里面并没有介绍到该算法，所以，这里我们也不予以介绍，感兴趣的小伙伴可以查阅相关资料或者直接看sklearn有关该算法的源码。

最后，我们还有两个证明没有说，接下来我们证明我们在上面提到的有关损失函数为平方损失时叶节点的最佳预测为叶节点的残差均值和损失函数为绝对损失时，叶节点的最佳预测为叶节点残差的中位数。

四. 附录

4.1 证明：损失函数为平方损失时，叶节点的最佳预测为叶节点残差均值

节点R中有N个样本点，假设s为切分点，，分别为切分后的左节点和右节点，分别有节点个数为。

我们的目标是找到切分点s，在，内部使平方损失误差达到最小值的，如下：

                              

和分别对求偏导，并令偏导等于0，得到在，内部使平方损失误差达到最小值的：

                              ，   

而和即为各自叶节点中的残差的均值。

4.2 证明：损失函数为绝对损失时，叶节点的最佳预测为叶节点残差的中位数。

损失函数

假设在节点中有个节点使，则有个节点使，那么：

                              

我们的目标是是损失函数最小化，所以，上式对求偏导，并令偏导等于0，得：

                              

得：

                             

而N为节点中样本的总数，所以使节点的最佳预测为节点中残差的中位数。

五. 参考文献/博文

（1）大牛Friedman关于梯度提升的论文

（2）《统计学习方法》第八章

（3）关于机器学习总结比较好的博客