K-mean(多维度)聚类算法(matlab代码)
申明: 仅个人小记
目录
- 效果演示
(1) 二维度效果图
(2) 三维度效果图 - k-mean 算法思想简要说明
- 代码分析
(1) 二维k-mean代码
(2) 三维度k-mean代码
(3) 多维度k-mean代码
(4) 功能使用示范代码
(5)后期函数接口改造(返回cell)
(6)新的函数接口使用范例 - 小结
一 . 效果演示
1. 二维度
(1) K = 6; 参与元素个数为1000

(2) K = 7; 参与元素个数为1000
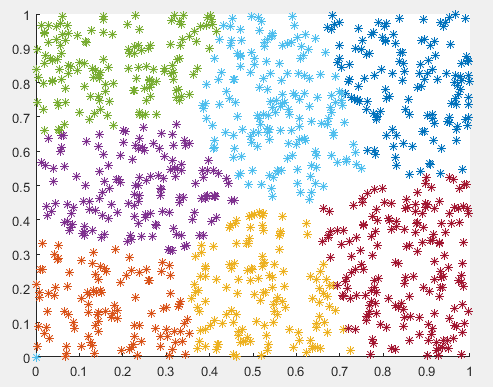
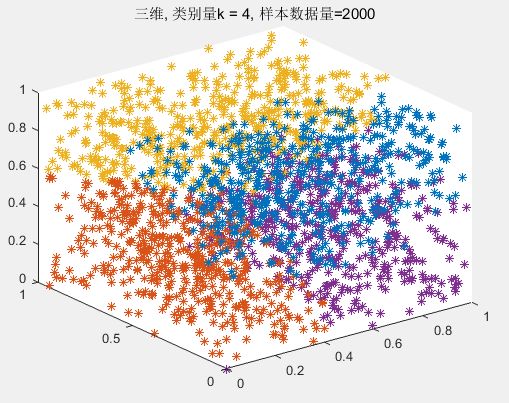
2. 三维度
(1)

(2)
2. k-mean 算法思想简要说明
给定1000个二维坐标点,现在指定要把它们分为k类,面对这样的情况该怎么处理?能想到的思路可能是穷举法,规规矩矩的从这1000个二维坐标点覆盖的二维面积中挑出k个点(我们称之为种子元素),然后遍历所有的元素点(这里指的就是1000个给定的点),对每一个元素进行判定类别,即判定每一个元素应该是归为k个类中哪一个类,并把该元素加入在被判定的类中。判断的规则就是,当前元素和k个种子之间的欧几里得距离最短的那个种子所代表的类就是当前元素应该加入的类。所有的元素遍历完毕,我们这是得到K组元素集合,即原来的元素被划分为k类了。这是我们计算每一组的方差,我目前认为应该是不停的用上述方法,得到分类,然后计算方差,最终,要找到每一个类方差最小的情况,这是认为是最优的分类,分类完毕。
显然,上述最大的弊端就是计算量很大,一点优化的成分都没有。k-mean算法思想中提出:但我们得到k组类别集合,计算k组每一组的中心点(方法就是计算均值点),每一组都得到中心点。这时,我们认为k组中心点为新的种子点。如果本次计算得到的种子点和之前的种子点是完全一致的,那么说明我们已经分类完毕了。如果不一致,如果不一致,我们就会基于的到的新的种子,再进行上述的操作,知道新计算的种子点和上一次的种子点完全匹配。另外,提一下关于第一次选择种子点的问题,应该是第一次选择的种子应该是来源于源数据样本元素(写代码的时候发现有必要这样做,如果不这样,在结果中会出现某一个类别的成员数量为0,显然,这是不合理的。成员个数为0的类别意味着这个类别是不存在,显然是不符合要分为k类的要求)。
3. 代码分析
(1) 二维度k-mean代码
function [ resX,resY,record] = FunK_mean( x,y,k )
% 功能:
% 实现k-mean聚类算法
% 输入:
% 二维数据,分别用x,y两个一维向量代表两个维度
% k 是分成的类别的数量
% 输出:
% k行的两个矩阵
% 对应同样的第n行,存放着第n类的所有元素
% record: 记录着每一行的有效元素的个数
j = 1;
% 下面是预分配一些空间
% seedX 和 seedY 中存放着所有种子
seedX = zeros(1,k);
seedY = zeros(1,k);
oldSeedX = zeros(1,k);
oldSeedY = zeros(1,k);
resX = zeros(k,length(x));
resY = zeros(k,length(x));
% 用来记录resX中每一行有效元素的个数
record = zeros(1,k);
for i = 1:k % 产生k个随机种子, 注意: 随机种子是来自元素集合
seedX(i) = x(round(rand()*length(resX)));
seedY(i) = y(round(rand()*length(resX)));
% 为保证种子不重叠
if (i > 1 && seedX(i) == seedX(i-1) && seedY(i) == seedY(i-1))
i = i -1; % 重新产生一个种子
end
end
seedX
seedY
while 1
record(:) = 0; % 重置为零
resX(:) = 0;
resY(:) = 0;
for i = 1:length(x) % 对所有元素遍历
% 下面是判断本次元素应该归为哪一类,这里我们是根据欧几里得距离进行类别判定
% k-mean算法认为元素应该归为距离最近的种子代表的类
distanceMin = 1;
for j = 2:k
if (power(x(i)-seedX(distanceMin),2)+power(y(i)-seedY(distanceMin),2))...
> (power(x(i)-seedX(j),2) + power(y(i)-seedY(j),2))
distanceMin = j;
end
end
% 将本次元素点进行类别归并
resX(distanceMin,record(distanceMin)+1) = x(i);
resY(distanceMin,record(distanceMin)+1) = y(i);
record(distanceMin) = record(distanceMin) + 1;
end
oldSeedX = seedX;
oldSeedY = seedY;
% 移动种子至其类中心
record
for i = 1:k
if record(i) == 0
continue;
end
seedX(i) = sum(resX(i,:))/record(i);
seedY(i) = sum(resY(i,:))/record(i);
end
% 如果本次得到的种子和上次的种子一致,则认为分类完毕。
if mean([seedX == oldSeedX seedY == oldSeedY]) == 1 % 这句话所想表达的意思就是 if seedX == oldSeedX && seedY == oldSeedY
break;
end
end
% 下面代码只是对resX,resY所占用的内寸大小进行简单的优化
maxPos = max(record);
resX = resX(:,1:maxPos);
resY = resY(:,1:maxPos);
end
(2) 三维度k-mean代码
function [ resX,resY, resZ,record] = FunK_mean3D( x,y,z,k )
% 功能:
% 实现三维空间k-mean聚类算法
% 输入:
% 三维数据,分别用x,y,z两个一维向量代表两个维度
% k 是分成的类别的数量
% 输出:
% k行的两个矩阵
% 对应同样的第n行,存放着第n类的所有元素
% record: 记录着每一行的有效元素的个数
j = 1;
% 下面是预分配一些空间
% seedX 和 seedY 中存放着所有种子
seedX = zeros(1,k);
seedY = zeros(1,k);
seedZ = zeros(1,k);
oldSeedX = zeros(1,k);
oldSeedY = zeros(1,k);
oldSeedZ = zeros(1,k);
resX = zeros(k,length(x));
resY = zeros(k,length(x));
resZ = zeros(k,length(x));
% 用来记录resX中每一行有效元素的个数
record = zeros(1,k);
for i = 1:k % 产生k个随机种子, 注意: 随机种子是来自元素集合
seedX(i) = x(round(rand()*length(resX)));
seedY(i) = y(round(rand()*length(resX)));
seedZ(i) = z(round(rand()*length(resX)));
% 为保证种子不重叠
if (i > 1 && seedX(i) == seedX(i-1) && seedY(i) == seedY(i-1) && seedZ(i) == seedZ(i-1))
i = i -1; % 重新产生一个种子
end
end
while 1
record(:) = 0; % 重置为零
resX(:) = 0;
resY(:) = 0;
resZ(:) = 0;
for i = 1:length(x) % 对所有元素遍历
% 下面是判断本次元素应该归为哪一类,这里我们是根据欧几里得距离进行类别判定
% k-mean算法认为元素应该归为距离最近的种子代表的类
distanceMin = 1;
for j = 2:k
if (power(x(i)-seedX(distanceMin),2)+power(y(i)-seedY(distanceMin),2)+power(z(i)-seedZ(distanceMin),2))...
> (power(x(i)-seedX(j),2) + power(y(i)-seedY(j),2)+power(z(i)-seedZ(j),2))
distanceMin = j;
end
end
% 将本次元素点进行类别归并
resX(distanceMin,record(distanceMin)+1) = x(i);
resY(distanceMin,record(distanceMin)+1) = y(i);
resZ(distanceMin,record(distanceMin)+1) = z(i);
record(distanceMin) = record(distanceMin) + 1;
end
oldSeedX = seedX;
oldSeedY = seedY;
oldSeedZ = seedZ;
% 移动种子至其类中心
record
for i = 1:k
if record(i) == 0
continue;
end
seedX(i) = sum(resX(i,:))/record(i);
seedY(i) = sum(resY(i,:))/record(i);
seedZ(i) = sum(resZ(i,:))/record(i);
end
% 如果本次得到的种子和上次的种子一致,则认为分类完毕。
if mean([seedX == oldSeedX seedY == oldSeedY seedZ == oldSeedZ]) == 1 % 这句话所想表达的意思就是 if seedX == oldSeedX && seedY == oldSeedY
break;
end
end
maxPos = max(record);
resX = resX(:,1:maxPos);
resY = resY(:,1:maxPos);
resZ = resZ(:,1:maxPos);
end
(3) 多维度k-mean代码
function [ res, record] = FunK_meanPolyD(data,k )
% 功能:
% 实现多维空间k-mean聚类算法
% 输入:
% data是d*n规格的矩阵,其中d代表维度,n代表样本的数量
% k 是分成的类别的数量
% 输出:
% res 是行数为(d*k), 列数为record中最大元素值
% 对于res的行数为d*k的解释:
% 1:d 是对应着第一类别元素
% d+1:2*d 是对应着第二类别元素
% ···
% d*(k-1)+1:d*k 是对应着第k类别元素
%
% record规格为1*k,记录着每一类别的有效元素的个数
j = 1;
% 下面是预分配一些空间
% seedX 和 seedY 中存放着所有种子
[h w] = size(data);
cnt = w; % 输入元素的数量
cntOfDimension = h; % d 中存放着本次处理数据的维度
%seed 中存放种子,每一行代表种子所在的一个维度,每一列是一个种子向量
seed = zeros(cntOfDimension,k);
oldSeed = zeros(cntOfDimension,k);
% 结果矩阵res中,数据存放规则:
% 以d行为一个单位,总共k个d行
% 第一个d行数据存放着第一类元素集合,其他同理
res = zeros(k*cntOfDimension,cnt);
% 用来记录resX中每一行有效元素的个数
record = zeros(1,k);
r = 0;
for i = 1:k % 产生k个随机种子, 注意: 随机种子是来自元素集合
t = round(rand()*cnt);
% 为保证种子不重叠
if i > 1 && t == r
i = i - 1;
continue;
end
seed(:,i) = data(:,t);
r = t;
end
while 1
record(:) = 0; % 重置为零
res(:) = 0;
for i = 1:cnt % 对所有元素遍历
% 下面是判断本次元素应该归为哪一类,这里我们是根据欧几里得距离进行类别判定
% k-mean算法认为元素应该归为距离最近的种子代表的类
distanceMin = 1; % distanceMin 中存放着最短欧几里得距离的种子点的下标
for j = 2:k
% 计算高维度的欧几里得距离
a = 0;
b = 0;
for row = 1:cntOfDimension
a = a + power(data(row,i)-seed(row,distanceMin),2);
b = b + power(data(row,i)-seed(row,j),2);
end
if a > b
distanceMin = j;
end
end
% 将本次元素点进行类别归并
row = (distanceMin-1)*cntOfDimension + 1;
res(row:row+cntOfDimension-1,record(distanceMin)+1) = data(:,i);
record(distanceMin) = record(distanceMin)+1;
end
%record
oldSeed = seed;
% 移动种子至其类中心
for col = 1:k
if record(col) == 0
continue;
end
% 计算新的种子位置
row = (col-1)*cntOfDimension + 1;
seed(:,col) = sum(res(row:row+cntOfDimension-1,:),2)/record(col);
end
% 如果本次得到的种子和上次的种子一致,则认为分类完毕。
if mean(seed == oldSeed) == 1
break;
end
end
maxPos = max(record);
res = res(:,1:maxPos);
end
(4) 功能使用示范
% k-mean算法在思想上还是存在弊端的
% k-mean算法是基于欧几里得空间距离进行基本判定的,而实际状况中不一定就是要以欧几里得空间距离作为判断基础的
% 下面是二维k-mean
clear all
close all
t = 1000;%指定样本元素个数
x = rand(1,t);% 产生样本数据
y = rand(1,t);
k = 7;% 指定类别数量
%
[resX,resY,record] = FunK_mean(x,y,k);% record 中存放着每一个类别组的成员数量
% 注意为了编写方便,resX,resY 是以二维矩阵的形式呈现
% resX(i,:) 和resY(i,:) 表示第i个类别组的所有成员,
% 但有效成员的数目不一定等于length(resX(i,:)),而是等于record(i)
% 多余的空位是用零来填充的
hold on
for i = 1:length(record)
plot(resX(i,1:record(i)),resY(i,1:record(i)),'*')
end
% 下面是标记出每一个类别的类别代表点
for i = 1:length(record)
plot(mean(resX(i,1:record(i)),2)',mean(resY(i,1:record(i)),2)','Marker','square','Color','k','MarkerFaceColor','k','LineStyle','none')
end
hold off
% % 三维度k-mean
%
% clear all
% close all
% t = 1000;
% x = rand(1,t);
% y = rand(1,t);
% z = rand(1,t);
% k = 5;
%
% [resX resY resZ record] = FunK_mean3D(x,y,z,k);
%
% for i = 1:length(record)
% plot3(resX(i,1:record(i)),resY(i,1:record(i)),resZ(i,1:record(i)),'*')
% hold on
% end
% % 下面是标记出每一个类别的类别代表点
% for i = 1:length(record)
% plot3(mean(resX(i,1:record(i)),2)',mean(resY(i,1:record(i)),2)',mean(resZ(i,1:record(i)),2)','Marker','square','Color','k','MarkerFaceColor','k','LineStyle','none')
% end
%下面是多维 k-mean演示部分,包括2维,3维度,高维度
clear all
close all
t = 2000;
d = 3;
data = rand(d,t);
k = 5;
[res, record] = FunK_meanPolyD(data,k);
[h, w] = size(res);
if h/k == 2
hold on
for i = 1:k
plot(res(i*2-1,1:record(i)),res(i*2,1:record(i)),'*')
plot(mean(res(i*2-1,1:record(i)),2),mean(res(i*2,1:record(i)),2),'Marker','square','Color','k','MarkerFaceColor','k','LineStyle','none')
end
hold off
elseif h/k == 3
for i = 1:k
plot3(res(i*3-2,1:record(i)),res(i*3-1,1:record(i)),res(i*3,1:record(i)),'*')
plot3(mean(res(i*3-2,1:record(i)),2),mean(res(i*3-1,1:record(i)),2),mean(res(i*3,1:record(i)),2),'Marker','square','Color','k','MarkerFaceColor','k','LineStyle','none')
hold on%注意:hold on 要写在plot3之后,这样三维图形才会正常绘制
end
hold off
else
disp(['结果维度大于3维,不能进行绘制'])
end
(5)后期函数接口改造 (借助matlab中cell结构实现)
function [res_cell, centroid] = FunK_meanPolyD(data,k )
% 输入:
% data : m * n m是数据的维度,n是数据的数量
% k : 类别数量
% 输出:
% res_cell: k个cell,每个cell中存放着该类别成员的在data中的下标
% centroid : 每个类别中心点 m*k 格式的矩阵,每一列代表一个类别的中心点
% 下面是预分配一些空间
% seedX 和 seedY 中存放着所有种子
[dim,n] = size(data);
%seed 中存放种子,每一行代表种子所在的一个维度,每一列是一个种子向量
seed = zeros(dim, k);
oldSeed = zeros(dim, k);
res = zeros(k,n);% k 行,一行代表一个类别,每一行存放成员标号(在data中的下标)
record = zeros(1,k);% 用来记录res 中每一行有效成员的个数
res_cell= cell(1,k);
%% 随机初始化种子,这里保证随机种子各不相同
tt = zeros(1,k);
for i = 1:k
flag = 1;
while flag
t = round(rand()*n);
flag = 0;
for j = 1:k
if t == tt(j)
flag = 1;
break;
end
end
end
tt(i) = t;
seed(:,i) = data(:,t);
end
%% 进入kmeans收敛过程
while 1
record(:) = 0; % 重置为零
for i = 1:n % 对所有元素遍历
distMin = 1; % distMin 中存放着最短欧几里得距离的种子点的下标
for j = 2:k
% 计算高维度的欧几里得距离
a = dot(data(:,i)-seed(:,distMin),data(:,i)-seed(:,distMin));
b = dot(data(:,i)-seed(:,j),data(:,i)-seed(:,j));
if a > b
distMin = j;
end
end
record(distMin) = record(distMin)+1;
res(distMin,record(distMin)) = i;
end
oldSeed = seed;
% 计算新的种子节点
seed(:) = 0;
for i = 1:k % 第i个类别
for j = 1:record(i) % 第i个别中的每个成员
seed(:,i) = seed(:,i) + data(:,res(i,j));
end
seed(:,i) = seed(:,i)/record(i); % 计算中心点
end
if seed == oldSeed
% 用cell对最后一次分组结果进行打包
for i =1:k
res_cell{1,i} = res(i,1:record(i));
end
centroid = seed;
break; % 退出kmeans收敛过程
end
end
end
(6)新的函数接口使用范例
close all
x = [1 1 2 2 4 5 5];
y = [1 2 1 3 5 5 3];
k = 2;% 指定类别数量
data = [x; y];
[dim, n] = size(data);
[res_cell,centroid] = FunK_meanPolyD(data,k)
figure;
for i = 1:k
t = res_cell{i};% t 中存放第i类别所有成员在原数据data中的下标
tt = data(:,t); % tt 则是根据t中提供的下标,在data中将第i类别成员全部取出来,放到tt中
if dim == 2 %绘制二维情况
plot(tt(1,:),tt(2,:),'*');
hold on
plot(centroid(1,i),centroid(2,i),'Marker','square','Color','k','MarkerFaceColor','k','LineStyle','none')
elseif dim == 3 % 绘制三维情况
plot3(tt(1,:),tt(2,:),tt(3,:),'*')
hold on
plot3(centroid(1,i),centroid(2,i),centroid(3,i),'Marker','square','Color','k','MarkerFaceColor','k','LineStyle','none')
end
grid on
end
4. 小结
(1) k-mean缺点: 需要指定k,并不能自动合理的对给定的数据进行分类
(2) 优点:思想还是很棒的,尤其是基于新的种子点进一步归类这一思想,这一步骤很好的利用了已经计算过的结果,而不是每一次都是从头开始。
(3) 如果能够自动分类,我觉得也可以这种能力划分到盲源分离领域了。
(4) k-mean算法在思想上还是存在弊端的。我是这样想的:k-mean算法是基于欧几里得空间距离进行基本判定的,而实际状况中不一定就是要以欧几里得空间距离作为判断基础的。这一想法的产生,是因为我想到了数字图像里面RGB空间模型里面,不能用欧几里得距离的大小来衡量两种颜色的相近程度。
2017年5月25日 23:59:35 By Jack Lu
