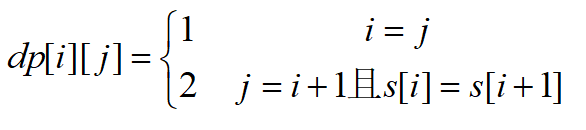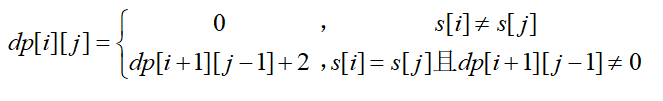最长回文子串——动态规划及Manacher算法解决

---

目录

1. 题目描述

2. 题目分析

2.1 动态规划法

2.1.1 原理分析

2.1.2 代码实现

2.1.3 复杂度分析

2.2 Manacher算法

2.2.1 原理分析

2.2.2 代码实现

2.2.3 复杂度分析

---

1. 题目描述

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

 

---

2. 题目分析

     题目很明确，就是找到一个字符串中最长的回文子串，暴力法这里就不多说了，下面介绍两种算法：动态规划法和Manacher法。

2.1 动态规划法

2.1.1 原理分析

       要使用动态规划法解决问题，那么就必须先把问题缩小为一个小问题，然后再从小问题往大问题扩展，最终解决大问题。动态规划往往需要借助一个数组dp来解决，其中非常重要的三点：dp数组元素的含义、dp数组的临界条件以及相应状态转移方程，临界条件可以看做是小问题的“起点”，而状态转移方程则是小问题向大问题扩展的依据。

       而在这道题目中，大问题是求整个字符串中的最长回文子串，而这里的最长则是各个回文子串长度中的最大值，因此，就可以将小问题看做是字符串s的回文子串的长度，就可以定义dp[i][j]来表示起点为i，终点为j的回文子串的长度。接下来，再来看dp数组的临界条件。不难得出，该问题的最小问题即是i=j的时候，由一个元素组成的字符串当然也是回文子串了，即dp[i][i]=1；另一种情况，当相邻两个元素相等时，即s[i]=s[i+1]时，那么dp[i][i+1]=2，由此可得dp数组的临界条件为：

                                                                       ，

       然后再来看状态转移方程，状态转移方程实际上就是将任意状态下的dp[i][j]用其子问题来表示，举个例子，dp[i][j]代表的是字符串i到j的回文子串的长度，当然，如果这个子串不是回文串，那么长度自然就是0了。与i到j最接近的回文子串即是i+1到j-1了，因此就可以将dp[i][j]用dp[i+1][j-1]表示来得到状态转移方程。如果s[i]不等于s[j]，那dp[i][j]当然长度就是0了；如果s[i]=s[j]，并且dp[i+1][j-1]不为零（即从i+1到j-1为回文子串），那么dp[i][j]就等于dp[i+1][j-1]+2了，如下：

                            

       分析完以上后，还需要注意状态转移方程的使用。前面说过，临界条件是问题的起点，因此应当从临界条件处开始慢慢扩展最终解决大问题。

2.1.2 代码实现

string longestPalindrome(string s) 
{
        int dp[1001][1001]={0}; 
        
        int len=s.size();       
        int start=0;    //保存最长子串的起点
        int max=1;   //保存最长子串的长度，初始化为1
        
        for(int i=0;i=0;i--)
            {
                if(s[i]==s[j]&&dp[i+1][j-1])
                    dp[i][j]=dp[i+1][j-1]+2;
                
                if(dp[i][j]>max) 
                {
                    max=dp[i][j];
                    start=i;
                }
            }
        } 
        string res(s.begin()+start,s.begin()+start+max);
        
        return res;
}

2.1.3 复杂度分析

       根据程序可以看出，动态规划实际上是对一个二维数组的一半进行遍历赋值，因此时间复杂度为O(N²)，同时也开辟了一段辅助空间，因此空间复杂度也为O(N²)。可见，动态规划的空间复杂度还是比较高的。

2.2 Manacher算法

2.2.1 原理分析

      Manacher算法是一种高效求解回文子串问题的方法。它是先用一种字符串中未曾出现过的字符来插空填入原字符串中，如：abcd->#a#b#c#d#，这样一来，假设原字符串长度为n，那么处理后的字符串长度就是2n+1，可以发现，这种方法不仅不会影响原字符串的回文性质，还巧妙地忽略了原字符串长度奇偶性带来的影响。

       然后Manacher算法还定义了一个辅助数组P，假设原字符串s经处理后变为了ss,那么P[i]表示以ss[i]为中心的回文串的半径，举个例子，s="cbabababd"，那么处理后的字符串ss="#c#b#a#b#a#b#a#b#d#"，对应的数组P如下：

P[0]

P[1]

P[2]

P[3]

P[4]

P[5]

P[6]

P[7]

P[8]

P[9]

P[10]

P[11]

P[12]

P[13]

P[14]

P[15]

P[16]

P[17]

P[18]

#

c

#

b

#

a

#

b

#

a

#

b

#

a

#

b

#

d

#

1

2

1

2

1

4

1

6

1

8

1

6

1

4

1

2

1

2

1

       那么，根据数组P又该怎么找到原数组中的最长回文子串呢？

根据数组P求出原字符串中最长回文子串长度：

        通过上面的表格，我们应该能理解数组P的含义了，那么这个数组有什么用呢？可以发现，P数组的最大值代表的是ss的最长回文子串的半径，假设最长半径为R，那么ss的最长回文子串长度为2*R-1，而这2*R-1长度的ss回文子串中，#号会比原字符多1个，去除多余的1个#号，再除以2，即是原数组s中的最长回文子串的长度了，最长回文子串长度为。

根据数组P求出原字符串中最长回文子串的首字符索引：

       知道了长度，要是再求得最长回文子串的首字符，那么就能得到该最长回文子串了。根据数组P，是很容易找到ss中最长回文子串的中心字符ss[i]以及其对应的回文半径P[i]的，那么i-P[i]+1就理应是回文子串的起点索引了，但是这里需要注意的是，在ss字符串中，回文子串的首末字符必定是‘#’，而原字符串s中并没有‘#’，而‘#’的下一个字符必定存在与s中，因此此时应当取‘#’的下一个字符，即索引加一。

       如表中的P[13]，计算其回文子串起点索引为13-4+1+1=11，即为'b'，那么'b'对应的s中的实际索引是多少呢？很简单，考虑到'b'前面的元素都是一半'#'一半原字符的，因此直接将ss中'b'的索引11减1除以2就得到了5，这就是'b'在原字符串中的索引。

       因此，如果原字符中的最长回文子串的起点索引为，其中i为ss中最长子串的中心索引。

       通过以上，即可根据P数组来找到原字符串中的最长回文子串了，那么接下来讲一下如何计算P数组。

       计算P数组各元素的时候需要考虑到回文子串的性质：关于中心元素镜像对称。还是观察P数组的表格，可以发现表中大部分元素都是关于P[9]对称的，对称的范围刚好就是(9-P[9],9+P[9])，在这个范围内的元素是对称的，这也就慢慢说明了一种可能：每个元素是可能受到其前面元素(回文半径较大并将元素包括在内)的影响的。这一点通过画图来说明：

       假设一个回文子串的中心索引为mid,其回文子串半径为R，那么其回文子串的最右端索引即是mid+R-1,假设在mid的右侧半径范围内有另一回文子串的中心索引为i，设其回文子串半径为r，那么就有两种情况：

①以i为中心的最长回文子串仍是以mid为中心的最长回文子串的子串。如图所示

                 

       在这种情况下，根据回文子串镜像对称的特点，必定能找到一个与以i为中心，r为半径的回文子串对称的回文子串，如图中的j，j=2*Mid-i那么此时P[i]就等于P[j]，即P[i]=P[2*Mid-i]；

②以i为中心的最长回文子串超出了以Mid为中心的最长回文子串右端，如图所示。

                 

       在这种情况下，以i为中心的回文子串和以j为中心的回文子串只有在(Mid-R,Mid+R)内的子串是相同的，之外是必定不同的（如果相同的话那以Mid为中心的最长子串就肯定更长了）。这个时候对于以i为中心的回文子串来说，超出Mid+R-1的部分是无法确定的，但是至少是大于等于Mid+R-i的，即r=P[i]≥Mid+R-i。此时要想确定P[i]，就需要从Mid+R开始进行匹配才能最终确定P[i]。

     综合i≤Mid+R-1的情况，不难得出，当Mid+R-i≥P[j]的时候，说明此时以i为中心的最长回文子串右端未超出Mid+R，因此P[i]=P[j]；否则就说明以i为中心的最长回文子串右端超出了Mid+R，此时就应当取P[i]=Mid+R-i，然后再进行匹配来确定P[i]。因此，当i位于Mid+R内时，P[i]=min(P[j],Mid+R-i)；

       当i超出了Mid+R时，那么就应当老老实实的进行匹配来确定P[i]的值了。

2.2.2 代码实现

string longestPalindrome(string s) {

        int len=s.size();
        
        int max_right=0;  //当前最大回文串的最右端
        int mid=0;  //当前最长回文串中心
        int start=0; //当前最长回文串的起点
        int max_length=0; //回文串最大长度
        int max_radius=0; //回文串最大半径
        
        string temp; //添加‘#’后的字符串

        temp+='+';
        temp+='#';
        for(auto c:s)
        {
            temp+=c;
            temp+='#';
        }
        temp+='-';  //前后加上特殊符号便于防止while越界
        
        len=2*len+3;
        
        int *radius=new int[len];
        
        radius[0]=1;
        
        for(int i=1;i=i说明以i为中心的回文串在以mid为中心max_right为半径的回文串内部，
              那么这两个回文串必定有交集，交集的大小就为min(max_right-i,radius[2*mid-i])*/
            
            if(max_right>=i)radius[i]=min(max_right-i,radius[2*mid-i]); 
            else radius[i]=1; //如果i不在max_right内，就初始半径为1，重新计数
            
            //计算i为中心的回文串半径
             //在temp前后添加'+'和'-'也是为了让这个while循环到字符串两端就退出
            while(temp[i-radius[i]]==temp[i+radius[i]])radius[i]++; 
            
            //如果以i为中心的回文串超过了max_right，则更新max_right
            if(i+radius[i]-1>max_right) 
            {
                max_right=i+radius[i]-1; //更新最大值

                mid=i;  //更新当前最长回文串的中心

                if(radius[i]>max_radius) //更新最大半径
                {
                    max_radius=radius[i];

                    start=(i-radius[i])/2; 
                    //计算对应的起点索引，这里因为前面多了一个‘+’，因此分子需要多减1
                }
            }
        }
        max_length=max_radius-1;
        
        string res(s.begin()+start,s.begin()+start+max_length);
        
        return res;
}

2.2.3 复杂度分析

       根据程序可以看出，程序中的max_right就是上文中提到的Mid+R-1，而算法时间复杂度主要是while循环，当i位于Mid+R内时，如果以i为中心的回文子串右端没有超出Mid+R,那么while是不会执行的，如果超出了Mid+R,那么while的执行效果是将max_right向右推进；当i位于Mid+R外时，毫无疑问，此时while的max_right也是向右推进，因此，整个程序实际上就是将max_right从0推到了len-1，时间复杂度就是O(N)。空间复杂度当然也是来源于数组P的O(N)了。

       这里需要说的一点是，可能会有人觉得这里的时间复杂度不是O(N)，因为感觉while会遍历左边的元素多次，并且还有for循环在外面。实际上，注意到while的循环条件，是左右两边同时遍历判断的，因此实际上在对左边一部分元素进行重复遍历所花的时间也就是向右推进max_right的时间，因此时间复杂度依然是O(N)。