漫画算法-小灰的算法之旅-排序算法(四)
1. 分类
1.1 时间复杂度为O(n^2)的排序算法
1.2 时间复杂度为O(nlogn)的排序算法
1.3 时间复杂度为线性的排序算法
1.4 稳定性
1.5 本文中涉及的排序总结
2. 冒泡排序
2.1 思想
2.2 代码实现
2.3 代码优化1
2.4 代码优化2
2.5 代码优化3
3. 快速排序
3.1 思想
3.2 基准元素的选择
3.3 单边循环法
3.4 双边循环法
3.5 栈实现
4. 堆排序
4.1 思想
4.2 代码实现
5. 计数排序
5.1 思想
5.2 代码实现
5.3 局限性
6. 桶排序
6.1 思想
6.2 代码实现
1. 分类
1.1 时间复杂度为O(n^2)的排序算法
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序(略优于O(n^2),但又低于O(nlogn),姑且归入本类)
1.2 时间复杂度为O(nlogn)的排序算法
- 快速排序
- 归并排序
- 堆排序
1.3 时间复杂度为线性的排序算法
- 计数排序
- 桶排序
- 基数排序
1.4 稳定性
如果值相同的元素在排序后仍然保持着排序前的顺序,那么这种排序算法是稳定排序,反之是不稳定排序。
1.5 本文中涉及的排序总结
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n^2) | O(n^2) | O(1) | 稳定 |
| 鸡尾酒排序 | O(n^2) | O(n^2) | O(1) | 稳定 |
| 快速排序 | O(nlogn) | O(n^2) | O(logn) | 不稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 计数排序 | O(n+m) | O(n+m) | O(m) | 稳定 |
| 桶排序 | O(n) | O(nlogn) | O(n) | 稳定 |
2. 冒泡排序
2.1 思想
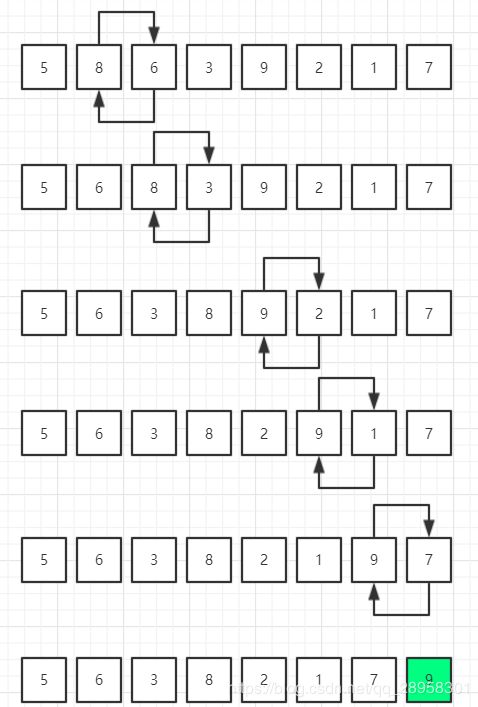
把相邻的元素两两比较,当一个元素大于右侧相邻元素时,交换它们的位置,当一个元素小于或等于右侧相邻元素时,位置不变。
例如以下待排序序列:
- 第1轮(详细)
- 第2轮-第7轮
2.2 代码实现
public class SortTest {
public static void bubbleSort(int[] array) {
//-1是因为最后一轮不需要排序
for (int i = 0; i < array.length - 1; i++) {
//-i是因为每一轮都能确定排序好一个数
for (int j = 0; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
//交换
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
}
public static void main(String[] args) {
int[] array = new int[]{5, 8 ,6, 3, 9, 2, 1, 7};
bubbleSort(array);
System.out.println(Arrays.toString(array));
}
}2.3 代码优化1
从上图中可以看出,第6轮排序后就已经是有序的了,可是算法还是进行了第7轮排序。
public class SortTest {
public static void bubbleSort1(int[] array) {
//-1是因为最后一轮不需要排序
for (int i = 0; i < array.length - 1; i++) {
boolean isSorted = true;
//-i是因为每一轮都能确定排序好一个数
for (int j = 0; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
//交换
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
//还在进行交换,表示未有序,还需要进行下一轮
isSorted = false;
}
}
if (isSorted) {
break;
}
}
}
public static void main(String[] args) {
int[] array = new int[]{5, 8 ,6, 3, 9, 2, 1, 7};
//bubbleSort(array);
bubbleSort1(array);
System.out.println(Arrays.toString(array));
}
}【注】因为序列原因,优化后的代码还是执行了7轮。作用情况是如果在第5轮结束的时候就已经有序了,那么程序只会进行到第6轮就停止,不会再进行第7轮,是这个意思。
2.4 代码优化2
参考以下待排序序列:
按照冒泡排序的思想,第1轮只会交换4和2、4和1的位置,第2轮只会交换3和2、3和1的位置...
说明的问题是:其实右边的许多元素已经是有序的了,但是程序不知道,他还是按照每一轮只会确定一个元素的顺序来执行,就造成了每一轮白白地比较了许多次。
public class SortTest {
public static void bubbleSort2(int[] array) {
//-1是因为最后一轮不需要排序
int sortedBorder = array.length - 1;
for (int i = 0; i < array.length - 1; i++) {
boolean isSorted = true;
int sortedBorder1 = sortedBorder;
for (int j = 0; j < sortedBorder1; j++) {
if (array[j] > array[j + 1]) {
//交换
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
//还在进行交换,表示未有序,还需要进行下一轮
isSorted = false;
//让下一轮不用比较右边有序的元素
sortedBorder = j;
}
}
if (isSorted) {
break;
}
}
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//bubbleSort(array);
//bubbleSort1(array);
bubbleSort2(array);
System.out.println(Arrays.toString(array));
}
}2.5 代码优化3
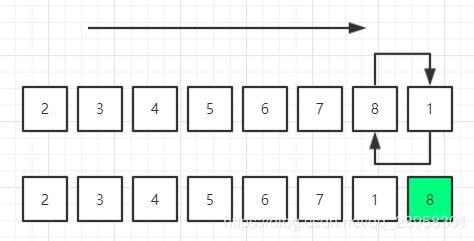
参考以下待排序序列:
按照冒泡排序的思想,第1轮只会交换8和1,第2轮只会交换7和1,第3轮只会交换6和1...
说明的问题是:2-8都是有序的,却要进行7轮排序。
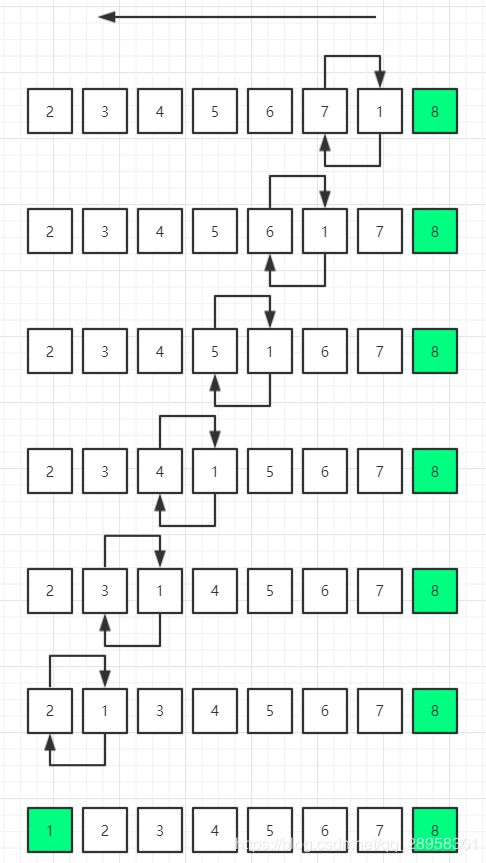
鸡尾酒排序:将单向的比较和交换变成双向的。
- 第1轮
- 第2轮
- 第3轮
虽然第2轮结束已经有序,但是程序还不知道,因为第2轮进行了交换,需要进行第3轮完全没有交换发生才说明已经有序,程序停止。
public class SortTest {
public static void bubbleSort3(int[] array) {
int sortedBorder = array.length - 1;
for (int i = 0; i < array.length - 1; i++) {
boolean isSorted = true;
int sortedBorder1 = sortedBorder;
if (i % 2 == 0) {
//从左往右
for (int j = 0; j < sortedBorder1; j++) {
if (array[j] > array[j + 1]) {
//交换
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
//还在进行交换,表示未有序,还需要进行下一轮
isSorted = false;
//让下一轮不用比较右边有序的元素
sortedBorder = j;
}
}
} else {
//从右往左
for (int j = sortedBorder1; j > 0; j--) {
if (array[j - 1] > array[j]) {
//交换
int temp = array[j - 1];
array[j - 1] = array[j];
array[j] = temp;
//还在进行交换,表示未有序,还需要进行下一轮
isSorted = false;
}
}
}
if (isSorted) {
break;
}
}
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
//bubbleSort(array);
//bubbleSort1(array);
//bubbleSort2(array);
bubbleSort3(array);
System.out.println(Arrays.toString(array));
}
}鸡尾酒排序的优点是能够在大部分元素已经有序的情况下,减少排序的回合数,而缺点就是代码量几乎增加了1倍。
3. 快速排序
3.1 思想
快速排序是在每一轮挑选一个基准元素,并让其他比它大的元素移动到序列的一边,比它小的元素移动到序列的另一边,从而把序列拆解成两个部分,这种思路叫分治法。
3.2 基准元素的选择
- 最简单的方式就是选择序列的第一个元素;
- 还可以随机选择一个元素,并和第一个元素交换位置。
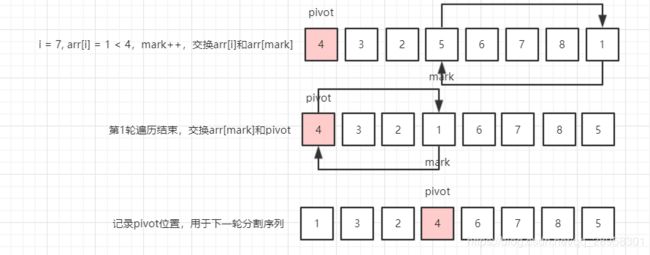
3.3 单边循环法
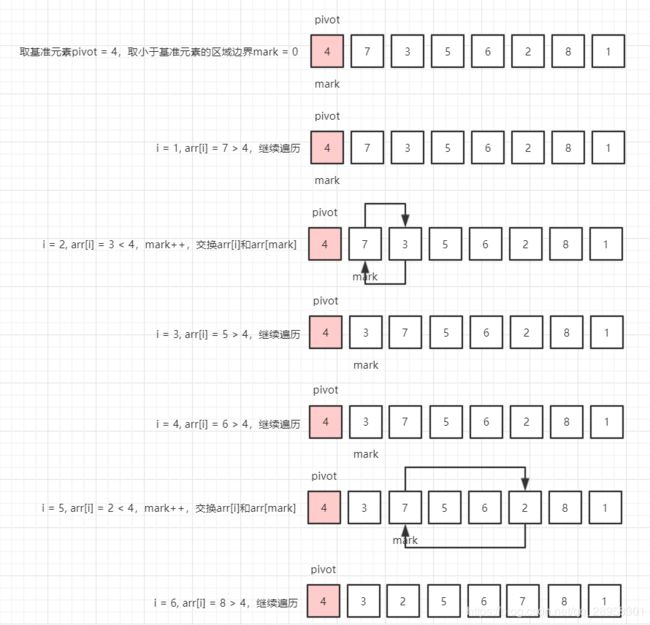
参考以下待排序序列:
- 第1轮
- 第2轮 - 结束
将由pivot分割的左、右序列分别遍历。
public class SortTest {
public static void quickSort(int[] array, int startIndex, int endIndex) {
//递归退出标志
if (startIndex >= endIndex) {
return;
}
//单边循环法
int pivotIndex = partition(array, startIndex, endIndex);
quickSort(array, startIndex, pivotIndex - 1);
quickSort(array, pivotIndex + 1, endIndex);
}
public static int partition(int[] array, int startIndex, int endIndex) {
//选取第1个元素为基准元素
int pivot = array[startIndex];
//小于基准元素的区域边界
int mark = startIndex;
for (int i = startIndex + 1; i <= endIndex; i++) {
if (array[i] < pivot) {
//该元素比基准元素小,需要放入区域,所以区域增大1
mark++;
//放入区域
int temp = array[mark];
array[mark] = array[i];
array[i] = temp;
}
}
//将基准元素交换到区域边界位置
array[startIndex] = array[mark];
array[mark] = pivot;
return mark;
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
//int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
int[] array = new int[]{4, 7, 3, 5, 6, 2, 8, 1};
quickSort(array, 0, array.length - 1);
System.out.println(Arrays.toString(array));
}
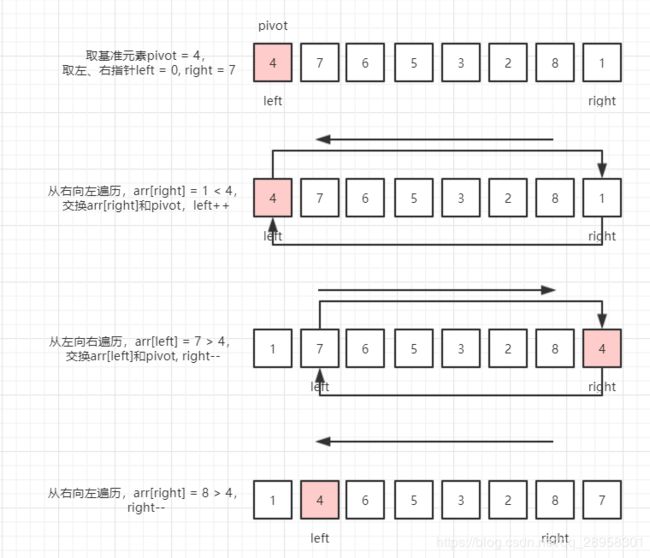
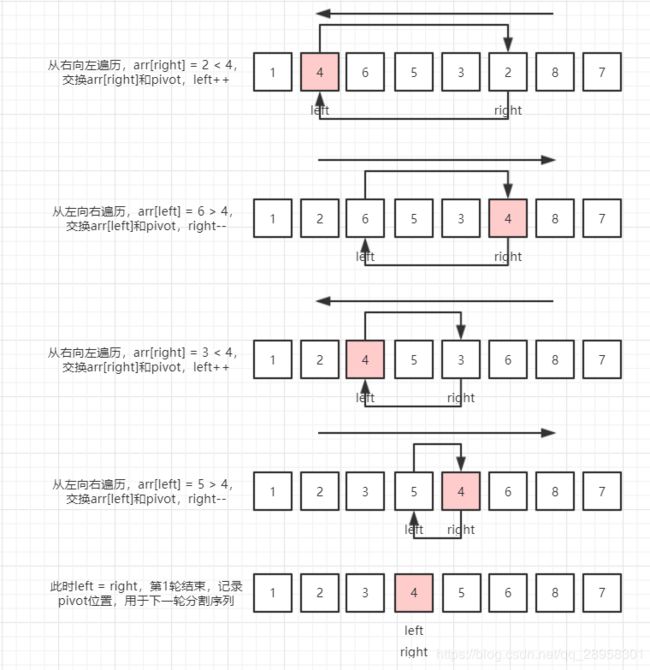
}3.4 双边循环法
参考一下带排序序列:
- 第1轮
- 第2轮 - 结束
将由pivot分割的左、右序列分别遍历。
public class SortTest {
public static void quickSort(int[] array, int startIndex, int endIndex) {
//递归退出标志
if (startIndex >= endIndex) {
return;
}
//双边循环法
int pivotIndex = partition1(array, startIndex, endIndex);
quickSort(array, startIndex, pivotIndex - 1);
quickSort(array, pivotIndex + 1, endIndex);
}
public static int partition1(int[] array, int startIndex, int endIndex) {
int pivotIndex = startIndex;
int left = endIndex;
int right = startIndex;
while (left != right) {
//从右向左
while (left > right) {
//如果右边的元素比基准元素小,那么交换,并且进行从左往右
if (array[left] < array[pivotIndex]) {
int temp = array[left];
array[left] = array[pivotIndex];
array[pivotIndex] = temp;
pivotIndex = left;
right++; //让从左往右不需要再比较一次刚才交换的元素
break;
} else {
left--;
}
}
//从左往右
while (left > right) {
//如果左边的元素比基准元素大,那么交换,并且进行从右往左
if (array[right] > array[pivotIndex]) {
int temp = array[right];
array[right] = array[pivotIndex];
array[pivotIndex] = temp;
pivotIndex = right;
left--; //让从右往左不需要再比较一次刚才交换的元素
break;
} else {
right++;
}
}
}
return left;
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
//int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
int[] array = new int[]{4, 7, 6, 5, 3, 2, 8, 1};
quickSort(array, 0, array.length - 1);
System.out.println(Arrays.toString(array));
}
}3.5 栈实现
栈实现区别只在于quickSort()方法实现,对于单边循环法、双边循环法并无影响。
public class SortTest {
public static void quickSortByStack(int[] array, int startIndex, int endIndex) {
//定义栈
Stack> stack = new Stack<>();
//第1轮入栈
Map map = new HashMap<>();
map.put("startIndex", startIndex);
map.put("endIndex", endIndex);
stack.push(map);
while (!stack.isEmpty()) {
//栈顶出栈
Map param = stack.pop();
//单边循环法,获取下一轮的两个序列的分界点
int pivotIndex = partition(array, param.get("startIndex"), param.get("endIndex"));
//左序列入栈
if (param.get("startIndex") < pivotIndex - 1) {
Map leftParam = new HashMap<>();
leftParam.put("startIndex", param.get("startIndex"));
leftParam.put("endIndex", pivotIndex - 1);
stack.push(leftParam);
}
//右序列入栈
if (pivotIndex + 1 < param.get("endIndex")) {
Map rightParam = new HashMap<>();
rightParam.put("startIndex", pivotIndex + 1);
rightParam.put("endIndex", param.get("endIndex"));
stack.push(rightParam);
}
}
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
//int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
int[] array = new int[]{4, 7, 6, 5, 3, 2, 8, 1};
quickSortByStack(array, 0, array.length - 1);
System.out.println(Arrays.toString(array));
}
} 4. 堆排序
4.1 思想
堆排序基于二叉堆的构建和删除,具体参考另一篇文章:
https://blog.csdn.net/qq_28958301/article/details/91590545#5.%C2%A0%E4%BA%8C%E5%8F%89%E5%A0%86
4.2 代码实现
public class SortTest {
public static void heapSort(int[] array) {
//构建最小堆
HeapTest.build(array);
//循环删除堆顶元素
for (int i = 0; i < array.length; i++) {
System.out.println(array[0]);
array = HeapTest.delete(array, 0);
}
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
//int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
//int[] array = new int[]{4, 7, 6, 5, 3, 2, 8, 1};
int[] array = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
heapSort(array);
//System.out.println(Arrays.toString(array));
}
}5. 计数排序
5.1 思想
计数排序是利用数组下标来确定元素的正确位置的。
5.2 代码实现
public class SortTest {
public static int[] countSort(int[] array) {
//得到序列的最大值和最小值,并计算差值d
int max = array[0];
int min = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
int d = max - min;
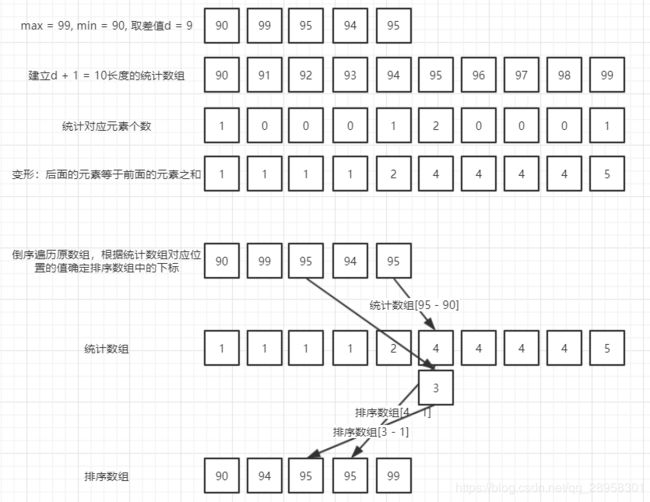
//创建统计数组并统计对应元素的个数
int[] countArray = new int[d + 1];
for (int i = 0; i < array.length; i++) {
countArray[array[i] - min]++;
}
//统计数组做变形,后面的元素等于前面的元素之和
//目的是让统计数组存储的元素值,等于相应整数的最终排序位置的序号
//例如:90, 99, 95, 94, 95序列,
//统计数组应该为:1, 0, 0, 0, 1, 2, 0, 0, 0, 1
//变形之后应该为:1, 1, 1, 1, 2, 4, 4, 4, 4, 5
//就可以轻易看出下标为9的元素99,最终的排序位置是在第5位
for (int i = 1; i < countArray.length; i++) {
countArray[i] += countArray[i - 1];
}
//倒序遍历原始序列,从统计数组中找到正确的位置,输出到结果数组
int[] sortedArray = new int[array.length];
for (int i = array.length - 1; i >= 0; i--) {
sortedArray[countArray[array[i] - min] - 1] = array[i];
//确定相同元素的位置
countArray[array[i] - min]--;
}
return sortedArray;
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
//int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
//int[] array = new int[]{4, 7, 6, 5, 3, 2, 8, 1};
int[] array = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
System.out.println(Arrays.toString(countSort(array)));
}
}5.3 局限性
- 当序列的最大值和最小值相差过大时,并不适合用计数排序;
- 当序列元素不是整数时,也不适合用计数排序。
6. 桶排序
6.1 思想
类似于计数排序所创建的统计数组,桶排序需要创建若干个桶来协助排序。
每一个桶代表一个区间范围,里面可以承载一个或多个元素。
6.2 代码实现
public class SortTest {
public static double[] bucketSort(double[] array) {
//得到序列的最大值和最小值,并计算差值d
double max = array[0];
double min = array[0];
for (int i = 1; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
double d = max - min;
//初始化桶
int bucketNum = array.length;
ArrayList> bucketList = new ArrayList<>();
for (int i = 0; i < bucketNum; i++) {
bucketList.add(new LinkedList<>());
}
//遍历原始数组,将每个元素放入桶内
for (int i = 0; i < array.length; i++) {
int num = (int) ((array[i] - min) * (bucketNum - 1) / d);
bucketList.get(num).add(array[i]);
}
//对每个桶内部进行排序
for (int i = 0; i < bucketList.size(); i++) {
//对引用类型,JDK内部采用归并排序
Collections.sort(bucketList.get(i));
}
//转换成数组并返回
double[] sortedArray = new double[array.length];
int index = 0;
for (LinkedList list : bucketList) {
for (double element : list) {
sortedArray[index++] = element;
}
}
return sortedArray;
}
public static void main(String[] args) {
//int[] array = new int[]{5, 8, 6, 3, 9, 2, 1, 7};
//int[] array = new int[]{3, 4, 2, 1, 5, 6, 7, 8};
//int[] array = new int[]{2, 3, 4, 5, 6, 7, 8, 1};
//int[] array = new int[]{4, 7, 6, 5, 3, 2, 8, 1};
//int[] array = new int[]{1, 3, 2, 6, 5, 7, 8, 9, 10, 0};
double[] array = new double[]{4.5, 0.84, 3.25, 2.18, 0.5};
System.out.println(Arrays.toString(bucketSort(array)));
}
}