数据结构与算法分析(C++)(第3版)-笔记二-线性表、栈和队列
1. 线性表的定义和基本操作的设计 与 其顺序存储结构和链式存储结构实现
定义：线性表 L 是 n 个数据元素 a0，a1，a2，......，an-1的有限序列，记作 L=(a0，a1，a2，......，an-1)。
其中元素个数n(n>=0)定义为表L的长度。当n=0时，L为空表，记作()。
第一个元素 a0 称为表头元素；
最后一个元素 an-1 称为表尾元素；
顺序表
定义：
采用连续的存储单元依次存储线性表中各元素，这种存储方式称为顺序存储方式，按这种存储方式所得到的线性表叫顺序表。
特点：
逻辑上相邻的元素在物理上一定相邻
ADT：
template <typename E> class List {
private:
int maxSize;
int listSize;
int curr;
E* listArray;
public:
List() {}
virtual ~List() {}
virtual void clear() = 0;
virtual void insert(const E& item) = 0;
virtual void append(const E& item) = 0;
virtual E remove() = 0;
virtual void moveToStart() = 0;
virtual void moveToEnd() = 0;
virtual void prev() = 0;
virtual void next() = 0;
virtual int length() const = 0;
virtual int currPos() const = 0;
virtual void moveToPos(int pos) const = 0;
virtual const E& getValue() const = 0;
}
基本操作：
- 插入操作
图示：
实现：
void insert(const E& it)
{
Assert(listSize<maxSize, "List capacity exceeded"); //边界检查
for(int i=listSize; i>curr; i--)
{
listArray[i] = listArray[i-1];
}
listArray[curr] = it;
listSize++;
}
- 删除操作
图示：
实现：
E remove()
{
Assert((curr>=0)&&(curr<listSize), "No element"); //边界检查
E it = listArray[curr];
for(int i=curr; i<listSize-1; i++)
{
listArray[i] = listArray[i+1];
}
listSize--;
return it;
}
链表
特点：
- 用一组任意的存储单元存储线性表的数据元素
- 利用指针实现了用不相邻的存储单元存放逻辑上相邻的元素
- 每个数据元素ai，存储 本身信息 + 其直接后继的信息
- 结点：
数据域：元素本身信息；
指针域：指示直接后继的存储位置；
ADT:
template <typename E> class Link {
public:
E element; //value for this node
Link *next; //Pointer to next node in list
Link(const E& elemval, Link* nextVval = NULL)
{
element = elemval;
next = nextval;
}
Link(link* nextval = NULL)
{
next = nextval;
}
}
单链表
template <typenmae E>
class LList: public list<E> {
private:
Link<E>* head;
Link<E>* tail;
Link<E>* curr;
int cnt;
void init(){
curr = tail = head = new Link<E>;
cnt = 0;
}
void removeall(){
while(head != NULL) {
curr = head;
head = head->next;
delete curr;
}
}
public:
LList(int size=DefaultListSize){
init();
}
~LList() {
removeall();
}
void clear() {
removeall();
init();
}
bool insert(const E& it);
bool append(const E& it);
E remove();
void moveToStart() {
curr = head;
}
void moveToEnd() {
curr = tail;
}
void prev();
void next();
int length() const {return cnt;}
int currPos() const;
void moveToPos(int pos);
const E& getValue() const;
}
基本操作
- 插入操作
1.创建新结点
2.新结点指向右边的结点
3.左边结点指向新结点
图示：
实现：
void insert(const E& it) {
// new Link(it, curr->next> -- 创建新的结点并赋给新值
curr->next = new Link<E>(it, curr->next>; //当前结点元素前驱的next域要指向新插入的结点
if(tail == curr)
tail = curr->next;
cnt++;
- 删除操作
示例(要删除p到x中间的元素)：
看起来似乎没什么问题，但是这样没有办法再找到想删除的元素了，也就是说它会一直保留在内存中，无法删除，浪费内存！
正确图示：
实现：
E remove() {
Assert(curr->next != NULL, "No element");
E it = curr->next->element;
link<E>* ltemp = curr->next;
if(tail == ltemp) tail = curr;
curr->next = curr->next->next;
delete ltemp;
cnt--;
return it;
}
循环链表
- 定义：循环链表是指表中最后一个结点的指针指向头节点，使链表构成环 状。
- 特点：从表中任一结点出发均可找到表中其它结点，提高查找效率。
- 操作与单链表基本一致，循环条件不同
单链表p：p->link = NULL;
循环链表p：p->link = H;
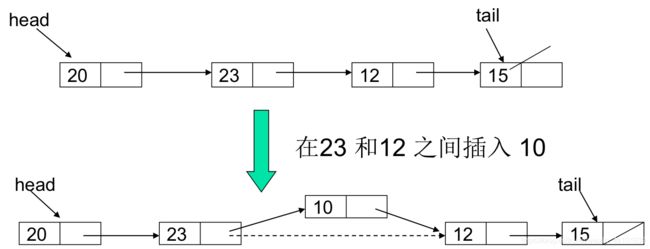
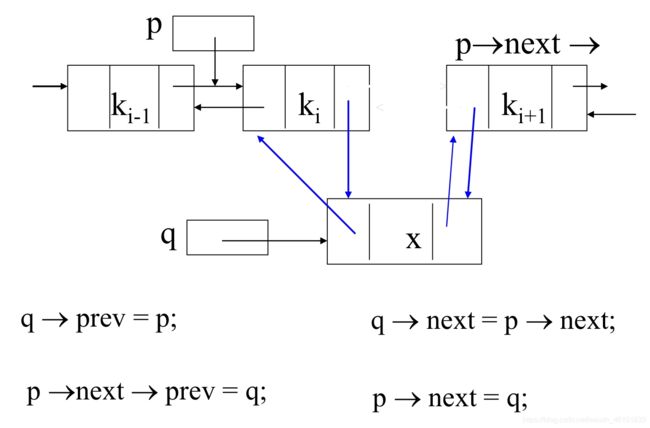
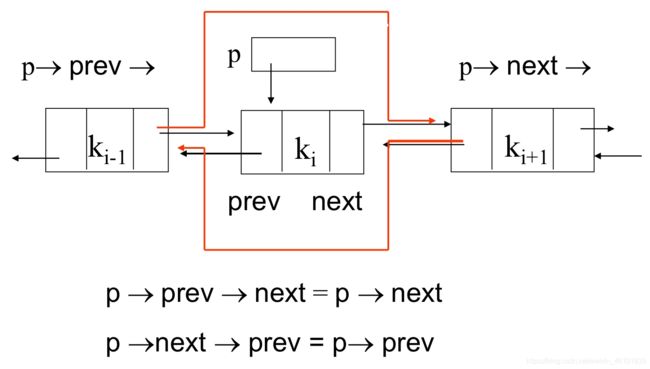
双链表
- 定义：双向链表是指在前驱和后继方向都能遍历的线性链表
- 结点结构：
- 双向链表通常采用带表头结点的循环链表形式
ADT：
template <typename E> class link {
private:
static link<E> *freelist;
public:
E element;
Link* next;
Link* prev;
Link(const E& it, Link* prevp, Link* nextp)
{
element = it;
prev = prevp;
next = nextp;
}
Link(Link* prevp = NULL, Link* nextp = NULL)
{
prev = prevp;
next = nextp;
}
void* operator new(size_t);
void operator delete(void*);
}
基本操作
- 插入操作
图示：
实现：
void insert(const E& it) {
curr->next = curr->next->prev = new Link<E>(it,curr,curr->next);
/**
* 等价于
* temp = new Link(it,curr,curr->next)
* curr->next->prev = temp;
* curr->next = temp;
*/
cnt++;
}
- 删除操作
图示：
实现：
E remove() {
if(curr->next == tail) return NULL;
E it = curr->next->element;
link<E>* ltemp = curr->next;
curr->next->next->prev = curr;
curr->next = curr->next->next;
delete ltemp;
cnt--;
return it;
}
线性表实现方法的比较
顺序表：
- 插入、删除运算的时间代价为O(n)；
- 需要预先申请固定长度的数组；
- 如果整个数组元素很满，则没有结构性存储开销
链表：
- 插入、删除运算的时间代价为O(1)；
- 存储利用指针，动态地按照需要为表中新的元素分配存储空间
- 每个元素都有结构性存储开销
顺序表和链表存储密度的临界值
2. 线性表的应用
顺序表
- 可大概估计结点总数目
- 线性表中结点较稳定（插入删除操作少）
- n > DE / (P+E)
链表
- 无法预知结点数目
- 线性表中结点动态变化（插入删除操作多）
- n < DE / (P+E)
判断给定的链表是以NULL结尾，还是形成一个环
-
蛮力法
-
Floyd 环判定算法
使用两个在链表中具有不同移动速度的指针，一旦它们进入环便会相遇，即表示存在环。
3. 栈和队列的基本概念和基本操作的设计 与 其顺序存储结构和链式存储结构实现
栈(stack)
- 只允许在一端插入和删除的线性表
- 允许插入和删除的一端称为栈顶(top)，另一端称栈底(bottom)
特点：
后进先出（ LIFO ）
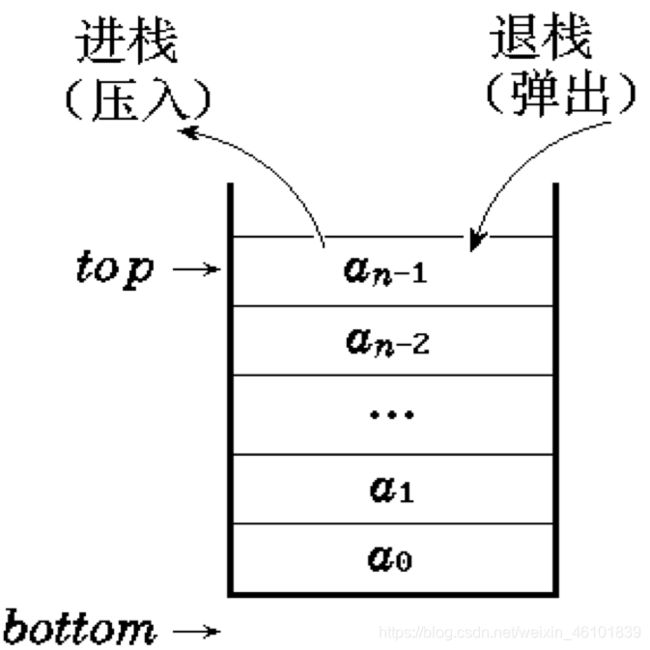
// 图中进栈和退栈反了
主要操作：
- 入栈 ( push )、出栈 ( pop )
- 取栈顶元素 ( topValue )
- 判栈空 ( isEmpty )
template <typename E> class AStack: public Stack<E> {
private:
int maxSize;
int top;
E* listarray;
public:
AStack(int size = DefaultListSize) {
maxSize = size;
top = 0;
listarray = new E[size];
}
~AStack() {
delete []listarray;
}
void clear() {
top = 0;
}
int length() const {
return top;
}
// 进栈
void push(const E& it) {
Assert(top != maxSize, "Stack is full");
listarray[top++] = it;
}
// 出栈
E pop() {
Assert(top != 0, "Stack is empty");
return listarray[--top];
}
Const E& topValue() const {
Assert(top != 0, "Stack is empty");
return listarray[top-1];
}
}
链式栈
template <typename E> class LStack: public Stack<E> {
private:
link<E>* top;
int size;
public:
LStack(int sz = DefaultListSize) {
top = NULL;
size = 0;
}
~LStack() {
clear();
}
void clear() {
whie(top != NULL) {
Link<E>* temp = top;
top = top->next;
delete temp;
}
size = 0;
}
int length() const {
return size;
}
// 进栈
void push(const E& it) {
top = new Link<E>(it, top);
size++;
}
// 出栈
E pop() {
Assert(top != NULL, "Stack is empty");
E it = top->element;
Link<E>* ltemp = top->next;
delete top;
top = ltemp;
size--;
return it;
}
Const E& topValue() const {
Assert(top != NULL, "Stack is empty");
return top->element;
}
}
过程的递归调用
递归过程及其实现 – 例：
Tower of Hanoi 汉若塔问题
算法：
递归函数示例：
函数调用及返回的步骤：
调用：
- 保存调用信息（参数，返回地址）
- 分配数据区（局部变量）
- 控制转移给被调用函数的入口
返回：
- 保存返回信息
- 释放数据区
- 控制转移到上级函数（主调用函数）
经典应用 ：
进制转换、括号匹配、迷宫求解、表达式求解：用于求解中缀表达式或者在前缀、中缀、后缀表达式间进行转换。
利用栈实现中缀转后缀：从左向右扫描中缀，遇到数字则加入后缀表达式，遇到运算符：
1.若是（则入栈
2.若是）则从栈中弹出运算符直到（
3.若是其他，则从栈中依次弹出优先级大于等于他的运算符，若遇到（则停止，然后将他入栈。
后缀表达式中（）不出现。
实现递归：多个函数嵌套调用的规则是：后调用先返回。
不是所有的递归程序都需要栈来保护现场，比方说求阶乘的，是单向递归，直接用循环去替代从1乘到n就是结果了，另外一些需要栈保存的也可以用队列等来替代。不是所有的递归转化为非递归都要用到栈。转化为非递归主要有两种方法：对于尾递归或单向递归，可以用循环结构算法代替。
队列（queue）
- 只允许在一端插入，在另一端删除的线性表；
- 允许插入的一端称为队尾(rear), 另一端为队首(front)
特点：
先进先出（FIFO）
主要操作：
- 入队 (enqueue)、出队(dequeue)
- 取队首元素(frontValue)
顺序队列：
实现：
用一维数组实现 sq[M]
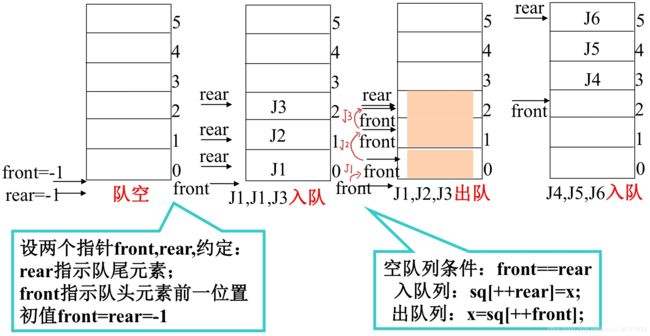
存在问题：
设数组维数为M，则
当 front = -1, rear = M-1 时，再有元素入队发生溢出 — 真溢出；
当 front != -1, rear = M-1 时，再有元素入队发生溢出 — 假溢出；
解决方案：
如何区别 队空 和 队满：
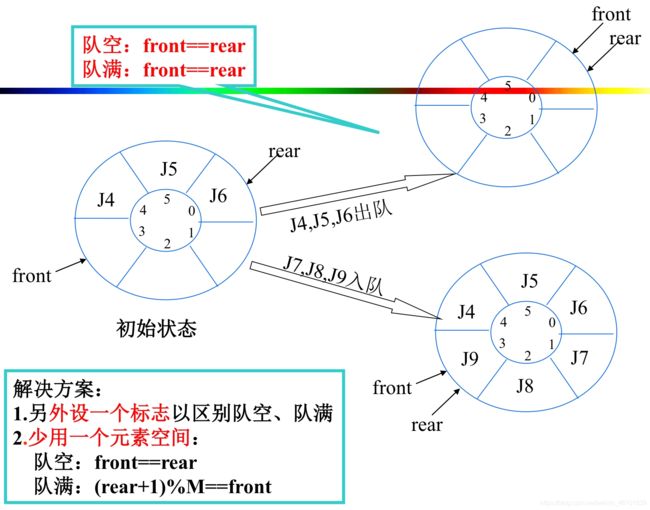
代码：
template <typename E> class AQueue: public Queue<E> {
private:
int maxsize;
int front;
int rear;
E* listArray;
public:
AQueue(int size = DefaultSize) {
maxsize = size + 1;
front = 1; //牺牲一个元素空间区分 队空 和 队满
rear = 0;
listArray = new E[maxsize];
}
~AQueue() {
delete []listArray;
}
void clear() {
front = 1;
rear = 0;
}
virtual int length() const {
return ( (rear + maxsize) - front + 1) % maxsize;
}
// 入队
void enqueue(const E& it) {
Assert(((rear+2)%maxsize != front), "Queue is full");
rear = (rear+1)%maxsize;
listArray[rear] = it;
}
// 出队
E dequeue() {
Assert(length() != 0, "Queue is empty");
E it = listArray[front];
front = (front+1)%maxsize;
return it;
}
const E& frontValue() const {
Assert(length() != 0, "Queue is empty");
return listArray[front];
}
}
链式队列
实现：
template <typename E> class LQueue: public Queue<E> {
private:
Link<E> *rear;
Link<E> *front;
int size;
public:
AQueue(int sz = DefaultSize) {
front = rear = new Link<E>();
size = 0;
}
~AQueue() {
clear();
delete front;
}
void clear() {
whie(front->next != NULL) {
rear = front;
front = front->next;
delete rear;
}
rear = front;
size = 0;
}
virtual int length() const {
return size;
}
// 入队
void enqueue(const E& it) {
rear->next = new Link<E>(it, NULL);
rear = rear->next;
size++;
}
// 出队
E dequeue() {
Assert(size != 0, "Queue is empty");
E it = front->next->element;
Link<E> *ltemp = front->next;
front->next = ltemp->next;
if(rear == ltemp) rear = front;
delete ltemp;
size--;
return it;
}
const E& frontValue() const {
Assert(size != 0, "Queue is empty");
return front->next->element;
}
}
例 – 识别图元
- 背景：
- 实例说明
- 算法说明
- 代码实现
void labelComponents() //给图元编号
{
//初始化数组offset
position offset[4];
offset[0].row=0;offset[0].col=1;
offset[1].row=1;offset[1].col=0;
offset[2].row=0;offset[2].col=-1;
offset[3].row=-1;offset[3].col=0;
//初始化0像素围墙
for(int i=0;i<=size+1;i++)
{
pixel[0][i]=pixel[size+1][i]=0;//底部和顶部
pixel[i][0]=pixel[i][size+1]=0;//左和右
}
int numOfNbrs=4;
//扫描所有像素，标记图元
arrayQueue<position>q;
position here,nbr;
int id=1;
for(int r=1;r<=size;r++)//从上到下
for(int c=1;c<=size;c++)//从左到右
if(pixel[r][c]==1)//发现新像元
{
pixel[r][c]=++id;//id增加1
here.row=r;//该像元设为种子点
here.col=c;
while(true)
{
for(int i=0;i<numOfNbrs;i++)//检查该种子点的所有领域
{//检查所有相邻位置
nbr.row=here.row+offset[i].row;
nbr.col=here.row+offset[i].col;
if(pixel[nbr.row][nbr.col]==1)
{
pixel[nbr.row][nbr.col]=id;
q.push[nbr]//将所有可标记领域插入队列
}
}
if(q.empty())break;
here=q.front();//寻找相应的邻域的邻域。直到队列为0.
q.pop();
}
}
}
图元识别详细可参考链接：https://blog.csdn.net/zj1131190425/article/details/88363509?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-5.control&dist_request_id=&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-5.control