tensorflow中关于 多维tensor的运算(tf.multiply, tf.matmul, tf.tensordot)
multiply 等同与* ,用于计算矩阵之间的element-wise 乘法,要求矩阵的形状必须一致(或者是其中一个维度为1),否则会报错:
import tensorflow as tf
a = tf.constant([1, 2, 3, 4, 5, 6, 7, 8, 9, 10,11,12], shape=[2, 3, 2])
b = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3, 1])
c = a*b
e = tf.multiply(a, a)
with tf.Session():
print(a.eval())
print(b.eval())
print(c.eval())
print(d.eval())
print(e.eval())
>> a
[[[ 1 2]
[ 3 4]
[ 5 6]]
[[ 7 8]
[ 9 10]
[11 12]]]
>>b
[[[1]
[2]
[3]]
[[4]
[5]
[6]]]
>>a*b
[[[ 1 2]
[ 6 8]
[15 18]]
[[28 32]
[45 50]
[66 72]]]
>>multiply(a, b)
[[[ 1 2]
[ 6 8]
[15 18]]
[[28 32]
[45 50]
[66 72]]]
>>multiply(a,a)
[[[ 1 4]
[ 9 16]
[ 25 36]]
[[ 49 64]
[ 81 100]
[121 144]]]
更改b的形状:
b=tf.constant([1,2,3,4,5,6], shape= [1,3,2])
d = a* b
with tf.Session():
print(a.eval())
print(b.eval())
print(d.eval())
>>a
[[[ 1 2]
[ 3 4]
[ 5 6]]
[[ 7 8]
[ 9 10]
[11 12]]]
>>b
[[[1 2]
[3 4]
[5 6]]]
>>c
[[[ 1 4]
[ 9 16]
[25 36]]
[[ 7 16]
[27 40]
[55 72]]]
b=tf.constant([1,2,3,4], shape= [2,1,2])
d = a* b
with tf.Session():
print(a.eval())
print(b.eval())
print(d.eval())
>>a
[[[ 1 2]
[ 3 4]
[ 5 6]]
[[ 7 8]
[ 9 10]
[11 12]]]
>>b
[[[1 2]]
[[3 4]]]
>>d
[[[ 1 4]
[ 3 8]
[ 5 12]]
[[21 32]
[27 40]
[33 48]]]
matmul 是tensor的矩阵乘法, 参与运算的两个tensor维度、数据类型必须一致,
参与运算的是最后两维形成的矩阵,如果tensor是二维矩阵,则等同于矩阵乘法:
# 二维tensor
a = tf.constant([1,2,3,4,5,6], shape=[2,3])
b = tf.constant([1,2,3,4,5,6], shape=[3,2])
c = tf.matmul(a,b)
with tf.Session():
print(a.eval())
print(b.eval())
print(c.eval())
>>a
[[1 2 3]
[4 5 6]]
>>b
[[1 2]
[3 4]
[5 6]]
>>c
[[22 28]
[49 64]]
# 三维tensor
a = tf.constant([i for i in range(1, 25)], shape=[2, 3, 4])
b = tf.constant([i for i in range(1, 25)], shape=[2, 4, 3])
c = tf.matmul(a, b)
>>a
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
>>b
[[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
[[13 14 15]
[16 17 18]
[19 20 21]
[22 23 24]]]
>>c
[[[ 70 80 90]
[ 158 184 210]
[ 246 288 330]]
[[1030 1088 1146]
[1310 1384 1458]
[1590 1680 1770]]]
# c形状[2,3,3],因为a的后两维是[3,4],b的后两维是[4,3],乘积为[3,3]
# 四维tensor
a = tf.constant([i for i in range(1, 25)], shape=[2, 2,2,3])
b = tf.constant([i for i in range(1, 25)], shape=[2, 2,3,2])
c = tf.matmul(a,b)
>>a
[[[[ 1 2 3]
[ 4 5 6]]
[[ 7 8 9]
[10 11 12]]]
[[[13 14 15]
[16 17 18]]
[[19 20 21]
[22 23 24]]]]
>>b
[[[[ 1 2]
[ 3 4]
[ 5 6]]
[[ 7 8]
[ 9 10]
[11 12]]]
[[[13 14]
[15 16]
[17 18]]
[[19 20]
[21 22]
[23 24]]]]
>>c
[[[[ 22 28]
[ 49 64]]
[[ 220 244]
[ 301 334]]]
[[[ 634 676]
[ 769 820]]
[[1264 1324]
[1453 1522]]]
# c的形状 [2,2,2,2]
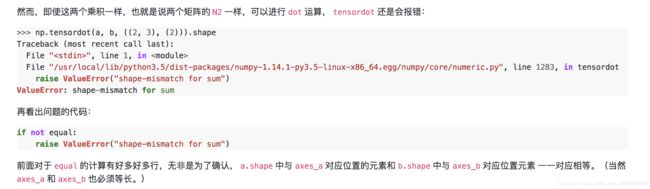
tensordot:矩阵乘法运算,参与运算的两个tensor的维度可以不一样:
a 和 b 沿特定轴的张量收缩.
Tensordot(也称为张量收缩)对从 a 和 b 所指定的索引 a_axes 和 b_axes 的元素的乘积进行求和.列表 a_axes 和 b_axes 指定沿其收缩张量的那些轴对.对于所有 range(0, len(a_axes)) 中的 i,a 的轴 a_axes[i] 必须与 b 的轴 b_axes[i] 具有相同的维度.列表 a_axes 和 b_axes 必须具有相同的长度,并由唯一的整数组成,用于为每个张量指定有效的坐标轴.
该操作对应于 numpy.tensordot(a, b, axes).
示例1:当 a 和 b 是矩阵(2阶)时,axes = 1 相当于矩阵乘法.
示例2:当 a 和 b 是矩阵(2阶)时,axes = [[1], [0]] 相当于矩阵乘法.
函数参数:
•a:float32 或 float64 类型的 Tensor.
•b:Tensor,与 a 具有相同的类型.
•axes:可以是标量 N,也可以是具有形状 [2,k] 的 int32 Tensor 的列表.如果轴是标量,则按顺序对 a 的最后 N 个轴和 b 的前 N 个轴进行求和.如果轴是一个列表或 Tensor,则分别对于轴 a 和 b,在第一和第二行包含该组唯一整数指定沿该收缩被计算.a 和 b 的坐标轴数必须相等.
•name:操作的名称(可选).
函数返回值:
函数返回与 a 具有相同类型的 Tensor.
可能引发的异常:
•ValueError:如果 a,b 和 axes 的形状是不相容的.
•IndexError:如果轴上的值超过相应张量的等级.
a = tf.constant([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], shape=[2,3,4])
b = tf.constant([1,2,3,4,5,6,7,8,9,10,11,12], shape=[4,3])
c = tf.tensordot(a, b, axes=1)
d = tf.tensordot(a, b, axes=2) # 对a的后2个轴乘积进行加和[2,3X4],即a的shape变成[2,12]; # 对b的前两个轴进行加和,b的shape变成[12]
e = tf.tensordot(a, b, axes=([1,2],[0,1]))
f = tf.tensordot(a, b, axes=([1,2],[1,0])) # 分别指定两个轴,对tensor进行展开,a展开成[2,12],
# b展开成[12,1],轴的顺序不同,展开方式不同
# 此处b展开成[1,4,7,10,2,5,8,11,3,6,9,12],上面展开成[1,2,3,4,5,6,7,8,9,10,11,12]
g = tf.tensordot(a, b, axes=([1],[1])) #指定任何轴,指定的轴形状一致
with tf.Session():
print(a.eval())
print(b.eval())
print(c.eval())
>>a
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
>>b
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
>>c
[[[ 70 80 90]
[158 184 210]
[246 288 330]]
[[334 392 450]
[422 496 570]
[510 600 690]]]
# c的形状 [2,3,3] [2,3,4] * [4,3]
>>d
[ 650 1586]
>>e
[ 650 1586]
>>f
[ 584 1520]
>>g
[[[ 38 83 128 173]
[ 44 98 152 206]
[ 50 113 176 239]
[ 56 128 200 272]]
[[110 263 416 569]
[116 278 440 602]
[122 293 464 635]
[128 308 488 668]]]
a = tf.constant([1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], shape=[2,3,4])
b = tf.constant([1,2,3,4,5,6,7,8,9,10,11,12], shape=[4,3])
c = tf.constant([1,2,3,4], shape=[4,1])
d = tf.tensordot(a, b, axes=1)
e = tf.tensordot(a, c, axes=1)
>>a
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
>>b
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
>>c
[[1]
[2]
[3]
[4]]
>>d
[[[ 70 80 90]
[158 184 210]
[246 288 330]]
[[334 392 450]
[422 496 570]
[510 600 690]]]
# d的形状[2,3,3] [2,3,4] * [4, 3] = [2,3,3]
>>e
[[[ 30]
[ 70]
[110]]
[[150]
[190]
[230]]]
# e的形状 [2,3,1] [2,3,4] * [4,1] = [2,3,1]
a = tf.constant([i for i in range(1, 25)], shape=[2,3,4])
b = tf.constant([i for i in range(1, 25)], shape=[2,2,6])
c = tf.tensordot(a,b,([1,2],[1,2]))
>>a
[[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]]
[[13 14 15 16]
[17 18 19 20]
[21 22 23 24]]]
>>b
[[[ 1 2 3 4 5 6]
[ 7 8 9 10 11 12]]
[[13 14 15 16 17 18]
[19 20 21 22 23 24]]]
>>c
[[ 650 1586]
[1586 4250]]
原文链接:点击获取原文
如果看完这个还是看不懂的,可以加QQ交流:2949710500