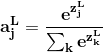【基于tensorflow的学习】线性回归、逻辑回归、神经网络

1.线性回归

线性回归属于机器学习当中的“回归学习”的一类。回归学习就是对于存在统计关系的变量，通过大量试验获得相关的统计数据，并构造目标函数去逼近该关系。主要的模型有：线性回归模型、多项式回归模型、主成分回归模型（采用PCA）、自回归模型、核回归模型。主要的求解回归模型的参数的方法有：最小二乘法、修正的Gauss-Newton法、有理插值法。

本章主要实现的是线性回归模型：

          (1.1)

代价函数--均方差（类似最小二乘法）:

        (1.2)

BP算法的参数求解：梯度下降法（类似求最小二乘法的微分方程以实现回归）

          (1.3)

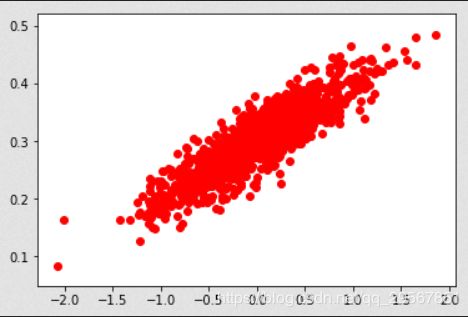
第一步，生成随机点：

import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
#随机生成1000个点，围绕在y0.1x+0.3直线的周围
num_points=1000
vector_set=[]
for i in range(num_points):
    x1=np.random.normal(0.0,0.55)#正态分布
    y1=x1*0.1+0.3+np.random.normal(0.0,0.03)
    vector_set.append([x1,y1])
    
#生成画图用的样本
x_data=[v[0] for v in vector_set]
y_data=[v[1] for v in vector_set]

#画图
plt.scatter(x_data,y_data,c='r')
plt.show()

第二步，构造tensor的计算图（变量、目标函数、损失函数、BP求解方法）：

#生成一维的W矩阵，取值是[-1,1]之间的随机数
W=tf.Variable(tf.random_uniform([1],-1.0,1.0),name='W')#name的作用：可以用来保存变量，日后想恢复的时候方便使用
#生成1维的b矩阵，初始值是0
b=tf.Variable(tf.zeros([1]),name='b')
#经过计算得出预估值y，得到的是一个大矩阵
y=W*x_data+b

#以预估值y和实际值y_data之间的均方误差作为损失
loss=tf.reduce_mean(tf.square(y-y_data),name='loss')
#采用梯度下降法来优化参数,并指定学习速率
optimizer=tf.train.GradientDescentOptimizer(0.5)
#训练的过程就是最小化这个误差值
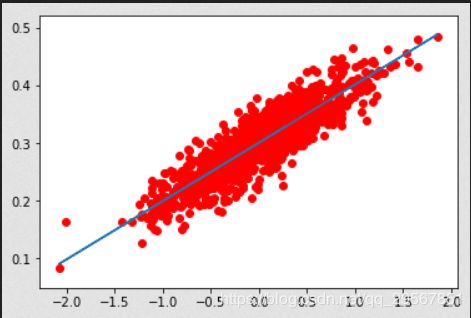
train=optimizer.minimize(loss,name='train')

第三步，开始计算并显示结果：

sess=tf.Session()
init=tf.global_variables_initializer()
sess.run(init)

#初始化的W和b是多少
print("W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss))
#执行20次训练
for step in range(20):
    sess.run(train)
    #输出训练好的W和b
    print("W=",sess.run(W),"b=",sess.run(b),"loss=",sess.run(loss))
plt.scatter(x_data,y_data,c='r')    
plt.plot(x_data,sess.run(W)*x_data+sess.run(b))
plt.show()

W= [0.87242603] b= [0.] loss= 0.26714
W= [0.64206684] b= [0.2943145] loss= 0.08926277
W= [0.47875005] b= [0.2962488] loss= 0.043957718
W= [0.36469984] b= [0.29762012] loss= 0.021863464
W= [0.28505418] b= [0.2985778] loss= 0.011088608
W= [0.22943452] b= [0.29924655] loss= 0.0058339597
W= [0.19059315] b= [0.29971358] loss= 0.0032713874
W= [0.16346872] b= [0.3000397] loss= 0.0020216794
W= [0.14452668] b= [0.3002675] loss= 0.0014122262
W= [0.1312987] b= [0.30042654] loss= 0.0011150095
W= [0.12206111] b= [0.30053762] loss= 0.00097006385
W= [0.11561014] b= [0.30061516] loss= 0.0008993772
W= [0.11110517] b= [0.30066934] loss= 0.0008649052
W= [0.10795919] b= [0.30070716] loss= 0.00084809394
W= [0.10576222] b= [0.3007336] loss= 0.00083989534
W= [0.104228] b= [0.30075204] loss= 0.0008358972
W= [0.10315659] b= [0.30076492] loss= 0.00083394727
W= [0.10240838] b= [0.30077392] loss= 0.00083299633
W= [0.10188588] b= [0.3007802] loss= 0.0008325326
W= [0.10152099] b= [0.3007846] loss= 0.0008323065
W= [0.10126618] b= [0.30078766] loss= 0.0008321961

 

2.逻辑回归

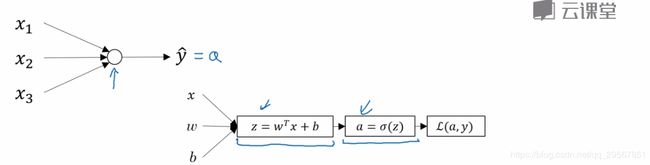
逻辑回归是一种分类算法。

若是二分类问题，则目标函数，即激活函数的选取为sigmoid函数：

      (2.1)

若为多分类问题，如手写数字的分类是十分问题，激活函数应为softmax函数：

          (2.2)

若代价函数依然选取均方差的话,带入a所得的函数为“非凸函数”，具有许多局部最小值，所以要选取一个合适的代价函数使得最优化的函数为“凸函数”，以求得全局最优解。

若为二分类问题，则使用cross-entropy交叉熵代价函数：

          (2.3)

就像是最大熵模型，保留全部的不确定性，将风险降到最小，则预测最准确。

使用交叉熵代价函数的想法起源可以看看这个：https://blog.csdn.net/zjuPeco/article/details/77165974

若为多分类问题，则使用log-likelihood对数似然代价函数：

         (2.4)

而BP算法依旧选用SGD。

若为二分类问题，则为：

      (2.5)

若为多分类问题，由于当y=0时，C=0，所以讨论i不等于j没有意义；故当y=1时，有：

      (2.6)

以下代码为minist手写数字识别：

第一步，载入数据：

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import input_data
#实际就是提取四个压缩包
mnist      = input_data.read_data_sets('data/', one_hot=True)
trainimg   = mnist.train.images
trainlabel = mnist.train.labels
testimg    = mnist.test.images
testlabel  = mnist.test.labels
#看看数据的大小
print ("MNIST loaded")
print (trainimg.shape)
print (trainlabel.shape)
print (testimg.shape)
print (testlabel.shape)
#print (trainimg)
print (trainlabel[0])

第二步，构造tensor的计算图：

x = tf.placeholder("float", [None, 784]) 
y = tf.placeholder("float", [None, 10])  # None is for infinite 
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
# LOGISTIC REGRESSION MODEL
actv = tf.nn.softmax(tf.matmul(x, W) + b) 
# COST FUNCTION
cost = tf.reduce_mean(-tf.reduce_sum(y*tf.log(actv), reduction_indices=1)) 
# OPTIMIZER
learning_rate = 0.5
optm = tf.train.GradientDescentOptimizer(learning_rate).minimize(cost)

# PREDICTION
pred = tf.equal(tf.argmax(actv, 1), tf.argmax(y, 1))   
# ACCURACY
accr = tf.reduce_mean(tf.cast(pred, "float"))
# INITIALIZER
init = tf.global_variables_initializer()

第三步，设置迭代的次数、mini-batch的大小等，并开始迭代并显示：

training_epochs = 50#50000个样本跑50次
batch_size      = 100#每次迭代用100个样本
display_step    = 5
# SESSION
sess = tf.Session()
sess.run(init)
# MINI-BATCH LEARNING
for epoch in range(training_epochs):
    avg_cost = 0.
    num_batch = int(mnist.train.num_examples/batch_size)
    for i in range(num_batch): 
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        sess.run(optm, feed_dict={x: batch_xs, y: batch_ys})
        feeds = {x: batch_xs, y: batch_ys}
        avg_cost += sess.run(cost, feed_dict=feeds)/num_batch
    # DISPLAY
    if epoch % display_step == 0:
        feeds_train = {x: batch_xs, y: batch_ys}
        feeds_test = {x: mnist.test.images, y: mnist.test.labels}
        train_acc = sess.run(accr, feed_dict=feeds_train)
        test_acc = sess.run(accr, feed_dict=feeds_test)
        print ("Epoch: %03d/%03d cost: %.9f train_acc: %.3f test_acc: %.3f" 
               % ((epoch+5), training_epochs, avg_cost, train_acc, test_acc))
print ("DONE")

学习速率	0.01	0.1	0.5	1.0	1.5	2.0	3.0	10.0	100.0
代价	0.306	0.246	0.202	0.177	nan	nan	nan	nan	nan
测试样本准确率	0.918	0.924	0.924	0.923	0.098	0.098	0.098	0.098	0.098

可见学习速率不是越高越好的，它是在一定范围值内才合适的，而为什么大的学习速率会导致cost无穷大呢？

答案就在BP算法里，我们更新权重w如下：

      (2.7)

如下图所示：

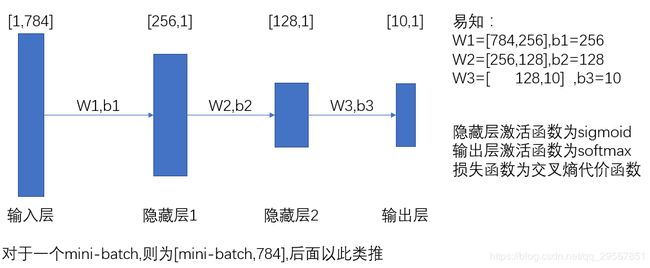
3.神经网络

这里实现一个简单的神经网络：一个输入层，两个隐藏层、一个输出层，如下图所示：

第一步，创建变量：

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import input_data
mnist = input_data.read_data_sets('data/', one_hot=True)
# NETWORK TOPOLOGIES
n_hidden_1 = 256 
n_hidden_2 = 128 
n_input    = 784 
n_classes  = 10  

# INPUTS AND OUTPUTS
x = tf.placeholder("float", [None, n_input])
y = tf.placeholder("float", [None, n_classes])
    
# NETWORK PARAMETERS
#正态分布初始化
stddev = 0.1
weights = {
    'w1': tf.Variable(tf.random_normal([n_input, n_hidden_1], stddev=stddev)),
    'w2': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2], stddev=stddev)),
    'out': tf.Variable(tf.random_normal([n_hidden_2, n_classes], stddev=stddev))
}
biases = {
    'b1': tf.Variable(tf.random_normal([n_hidden_1])),
    'b2': tf.Variable(tf.random_normal([n_hidden_2])),
    'out': tf.Variable(tf.random_normal([n_classes]))
}

第二步，创建前向传播：

#前向传播
#sigmoid函数作为激活函数
def multilayer_perceptron(_X, _weights, _biases):
    layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(_X, _weights['w1']), _biases['b1'])) 
    layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, _weights['w2']), _biases['b2']))
    return (tf.matmul(layer_2, _weights['out']) + _biases['out'])#最后一个输出层不是sigmoid，只要输出z=wx+b即可 

第三步，创建反向传播：

其中tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=pred)具体使用可参照：https://blog.csdn.net/yhily2008/article/details/80262321

#反向传播
# PREDICTION
pred = multilayer_perceptron(x, weights, biases)#[128*mini-batch,10]

# LOSS AND OPTIMIZER
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=pred))#y=[mini-batch,10] 
optm = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) 
corr = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))    
accr = tf.reduce_mean(tf.cast(corr, "float"))

# INITIALIZER
init = tf.global_variables_initializer()

第四步，设置迭代的次数、mini-batch的大小等，并开始迭代并显示：

training_epochs = 20
batch_size      = 100
display_step    = 4
# LAUNCH THE GRAPH
sess = tf.Session()
sess.run(init)
# OPTIMIZE
for epoch in range(training_epochs):
    avg_cost = 0.
    total_batch = int(mnist.train.num_examples/batch_size)
    # ITERATION
    for i in range(total_batch):
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        feeds = {x: batch_xs, y: batch_ys}
        sess.run(optm, feed_dict=feeds)
        avg_cost += sess.run(cost, feed_dict=feeds)
    avg_cost = avg_cost / total_batch
    # DISPLAY
    if (epoch+1) % display_step == 0:
        print ("Epoch: %03d/%03d cost: %.9f" % (epoch, training_epochs, avg_cost))
        feeds = {x: batch_xs, y: batch_ys}
        train_acc = sess.run(accr, feed_dict=feeds)
        print ("TRAIN ACCURACY: %.3f" % (train_acc))
        feeds = {x: mnist.test.images, y: mnist.test.labels}
        test_acc = sess.run(accr, feed_dict=feeds)
        print ("TEST ACCURACY: %.3f" % (test_acc))