记一下机器学习笔记 核方法与径向基函数网络

这里算是《神经网络与机器学习》第5章的笔记。
其实本章主打的是还是径向基函数，关于核方法的内容不多。

核方法的想法就是，把原来线性不可分的样本通过某种非线性变换映射到合适的高维特征空间，使之方便用线性学习器来处理。
径向基函数网络是一种实现方式，其结构类似于单一隐藏层的神经网络，原理是在隐藏层用径向基函数将数据映射到高维特征空间，然后再在输出层对其输出进行线性分类。
这招最经典的应用便是支持向量机。

Cover定理

Cover定理说白了就是：把一堆线性不可分的数据非线性地映射到一个维度更高的空间，没准就变得线性可分了。

首先，输入的数据样本集为一组N个 m0 维的向量 x1,x1,...,xN ，每个样本都被归类到两个类 C1 和 C2 之一。
定义一组实值函数（也就是输入一个向量输出一个实数的函数） φ1(x),φ2(x),...,φm1(x) ，用来将输入数据映射到一个 m1 维的空间，将它们组成一个向量：

ϕ=[φ1(x),φ2(x),⋯,φm1(x)]T

这个函数向量 ϕ 的输出可被认为是被映射到高维空间之后的输入数据 x 。 φi(x) 称为隐藏函数，其组成的向量 ϕ 所在的空间称为隐藏空间或特征空间。

如果有那么个 m1 维的向量 w ，使得这个成立：

wTϕ(x)>0,x∈C1;

wTϕ(x)<0,x∈C2;

也就是说被 ϕ 映射到另一个高维空间的数据样本们成了线性可分的，就说这个把 x 分类到 C1 和 C2 的分法是 ϕ 可分的。
对于 x 来说， wTϕ(x)=0 就是一个分类曲面。

于是模式可分性的Cover定理在这就包含这两部分：

• 隐藏函数的非线性转换。
• 高维的特征空间（这个高维是相对原始数据的维度来说的，由隐藏函数的个数决定）。

异或问题

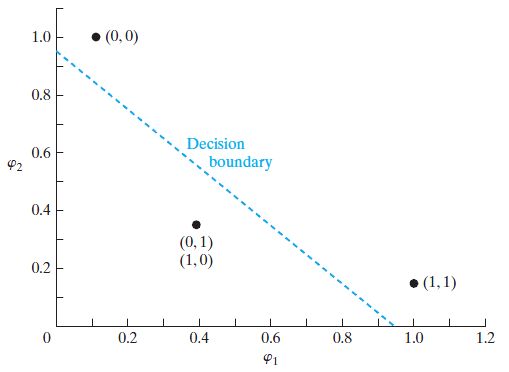
拿异或问题举个栗子。因为是个典型的线性不可分问题。
其点(0,0)和(1,1)归于类0，点(0,1)和点(1,0)归于类1。

然后我们要拿一组隐藏函数将这些点映射到零一空间里。
在这里使用高斯隐藏函数。因为问题简单，所以只用了两个隐藏函数，维度没有增加，不过够用了：

φ1(x)=exp(−∥x−t1∥2)

φ2(x)=exp(−∥x−t2∥2)

其中 t1=(1,1) ， t2=(0,0) 。也就是拿样本点跟这俩点的几何距离作为高斯函数的自变量。
转换出来这个样子。

转换前	转换后
(1,1)	(1.0000, 0.1353)
(0,1)	(0.3678, 0.3678)
(0,0)	(0.1353, 1.0000)
(1,0)	(0.3678, 0.3678)

图画出来一看，线性可分了。

这就是传说中的核技巧。

径向基函数网络

插值问题

其实单一输出变量的机器学习问题可以理解成这么一个插值问题（可以拿地统计里的空间插值理解）：

• 训练阶段就是找出这么个曲面：
  F(xi)=di,i=1,2,⋯,N
• 泛化阶段就是在这曲面上插值。

这里用的解决方案就是径向基函数（Radial-Based Function，RBF）技术。
其给出的 F(x) 的形式为：

F(x)=∑i=1Nwiφi(∥x−xi∥)

径向基函数，也就是 RBF，就是形式为 φi(∥x−xi∥) 的函数。
其接受的自变量为一个向量，函数本身具备一个维数同自变量的向量（就是那个 xi ），其称为函数的 中心。
先计算出自变量和中心的欧几里得范数（也就是几何距离），再将其放进外边的函数 φ 。
这样获得的函数形状呈中心对称的放射状，所以叫径向基函数。

上边两个式子合在一起就变成：

∑i=1Nwiφi(∥xi−xj∥)=di,i=1,2,⋯,N

或者写成矩阵形式：

Φw=d

其中 Φ 为插值矩阵：

Φ=⎡⎣⎢⎢⎢⎢⎢φ11φ21⋮φN1φ12φ22⋮φN2⋯⋯⋱⋯φ1Nφ2N⋮φNN⎤⎦⎥⎥⎥⎥⎥

其中 φij=φ(∥xi−xj∥) ，这里 xj 并不是样本而是函数中心。

w 为出现过很多次的权值向量。 d 则为期望向量 [d1,d2,⋯,dN]T 。
于是可以解得权值向量 w=Φ−1d 。

接下来问题就是插值矩阵 Φ 如何保证是非奇异的，也就是可以求逆矩阵。

Micchelli定理

Micchelli定理的内容说白了就是，只要每个样本点都是空间中互不相同的点，那么求出来的插值矩阵 Φ 就是非奇异的。

以下的几个径向基函数都满足Micchelli定理：

φ(r)=r2+c2−−−−−−√对某些c>0

φ(r)=1r2+c2−−−−−−√对某些c>0

φ(r)=exp(−r22σ2)对某些σ>0

其中 r 即为样本跟函数中心的欧几里得范数 ∥xi−xj∥ 。
上边第三个就是出镜率最高的 高斯函数，正态分布的密度函数也是其变式。

径向基函数网络

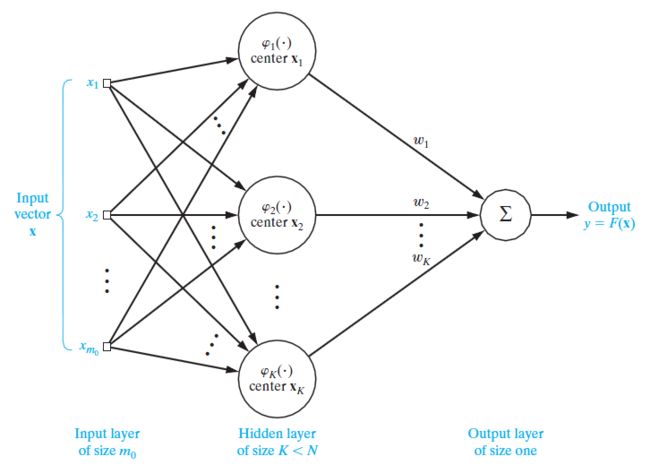
有了以上的内容就可以构造径向基函数网络了。其跟单隐藏层的神经网络类似，一共三层：

• 输入层。结点数量为输入数据的维数 m0 。
• 隐藏层。其结点跟神经网络的不同之处在于是激活函数就是径向基函数，并且不带权值。在这里径向基函数用高斯函数：
  φ(r)=exp(−∥x−xi∥22σ2)
  于是其结点也叫高斯隐藏单元。一般情况下参数 σ （也称为宽）用的都是同一个，而中心 xi 则不一样。
• 输出层。对隐藏层传过来的信号加权求和作为输出： y=∑Ni=1wiφi 。

根据前边的理论，隐藏层的结点，也就是高斯隐藏单元的数量应该跟样本数一样多，都是N。但是实际上为避免冗余和过拟合，高斯隐藏单元数量都取一个比N要小的数K，如下图。

使用K-Means聚类找中心

给隐藏函数找参数，比如给径向基函数找中心的时候用的一般是无监督学习方法。而在这里用的则是K-Means聚类方法，将聚出来的K个类的中心作为K个高斯隐藏单元的中心。

理由大概是聚类的目标是最大化聚出来的类之间的差异＆最小化类内元素的差异，并且K-Means中用的距离计算属于非线性转换，这样把样本点映射到高维空间之后线性可分的概率较高。

还有个理由就是，K-Means聚类简单粗暴效率高，还挺有效的。

递归最小二乘算法

搞定了隐藏层之后就剩下输出层的权值向量 w 。
到了这里就变成了一个《神机》的LMS算法那章的问题，只不过样本矩阵 X 换成了映射以后的样本，也就是插值矩阵 Φ 。
所以那章里给出的最小二乘滤波方法可以改写成这个样子：

w=(ΦTΦ)−1ΦTd

用这个可以一次性计算出最优的权值向量。
实际情况中 Φ 为N行K列的矩阵：

Φ=⎡⎣⎢⎢⎢⎢⎢φ11φ21⋮φN1φ12φ22⋮φN2⋯⋯⋱⋯φ1Kφ2K⋮φNK⎤⎦⎥⎥⎥⎥⎥

φij=exp(−∥xi−kj∥22σ2)

这里 kj 为函数中心， j=1,2,⋯,K 。

不过一般情况下，高斯隐藏单元数K虽然比样本数N要小，但还是一个比较大的值，所以一次性计算的计算量还是挺大的。另外在LMS算法的那章里的随机梯度方法实验也可以得知，很多时候一轮迭代还没迭代完就收敛了，所以这里应该可以找一个逐个样本迭代调整权值的方法。
于是就有了递归最小二乘（Recursive Least-Squares，RLS）算法。

在这里把最小二乘的公式改写一下：

Rw=r

R=ΦTΦ,r=ΦTd

再将 R 跟 r 改写一下可以变成迭代的形式：

R(i)=∑j=1iϕTjϕjϕj=[φj1,φj2,⋯,φjK]T

r(i)=∑j=1iϕjdj

ϕj 就是第j个被映射后的样本。

这样就有：

r(i)=∑j=1i−1ϕjdj+ϕidi=r(i−1)+ϕidi=R(i−1)w(i−1)+ϕidi

最右边的两项分别加上和减去一个 ϕTiϕiw(i−1) 变成：

r(i)=[R(i−1)+ϕTiϕi]w(i−1)+ϕi[di−ϕTiw(i−1)]

再进一步写成：

r(i)=R(i)w(i)=R(i)w(i−1)+ϕiα(i)

其中 α(i) 成为先验估计误差， α(i)=di−ϕTiw(i−1) 。

于是权值向量就可以写成迭代的形式：

w(i)=w(i−1)+R(i)−1ϕiα(i)

然后就是 R−1 怎么求。
根据逆矩阵引理：如果

A=B−1+CDCT

那么

A−1=B−BC(D+CTBC)−1CTB

令 A=R(i) ， B−1=R(i−1) ， C=ϕ(i) ， D=1 ，利用 R(i) 的对称性，并令 P(i)=R(i)−1 可得：

P(i)=P(i−1)−P(i−1)ϕ(i)ϕT(i)P(i−1)1+ϕT(i)P(i−1)ϕ(i)

综上，RLS算法过程如下：

1. 设置初始值， w(0)=0 ， P(0)=λ−1I （ λ 为小的正常数）
2. 计算 P(i) ：
   P(i)=P(i−1)−P(i−1)ϕ(i)ϕT(i)P(i−1)1+ϕT(i)P(i−1)ϕ(i)
3. 计算 α(i) ：
   α(i)=di−ϕTiw(i−1)
4. 更新 w ：
   w(i)=w(i−1)+P(i)ϕiα(i)
5. 回到2接着下一步，直到收敛。

R代码实验

我发现这本书的作者真的很喜欢这个双月牙形状。后面的支持向量机一章依然是用它做实验。

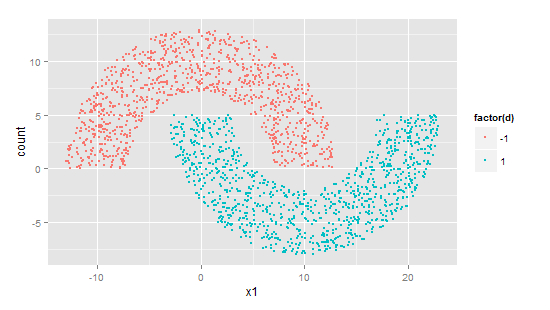
具体生成实现在感知机的那章。这里俩月牙的距离为-5。

首先定义高斯径向基函数。

phi = function(x,xi,sigma) exp(-(t(x-xi)%*%(x-xi))/(2 * sigma**2))

然后就是使用K-Means聚类定中心。R自带K-Means的相关函数，可以直接调用。

K = 20 #高斯单元数目，也就是聚类中心为20个。

#X为双月牙点坐标集，点数N=2000。
#使用K-Means确定中心坐标。
cnt = kmeans(X,K)['centers'][[1]]

函数的宽定为中心的散布情况，即

σ=dmax2K−−−√

dmax 为中心间的最大距离。

sigma = max(dist(cnt))/sqrt(2*K)

然后就是通过隐藏层将输入数据映射到高维空间。

#用了两层apply，看上去有点混乱，但其实内层的apply是用高斯径向基函数
#将一个样本映射到高维空间，外层的apply则是对每一个样本使用这个映射。
Phi=t(apply(X,1,function(x)
  apply(cnt,1,function(xi)phi(x,xi,sigma)))
)

之后就是找出最优的输出层权值向量 w 。
先用LMS的最小二乘滤波方法的公式一次性计算。

W = solve(t(Phi) %*% Phi) %*% t(Phi) %*% d

然后是获得和输出分类结果。

y = sign(Phi %*% W)

> length(y[y!=d])/length(y)*100
[1] 0.05

可知误分类率只有0.05%（大概就是只有一个点分错了）。

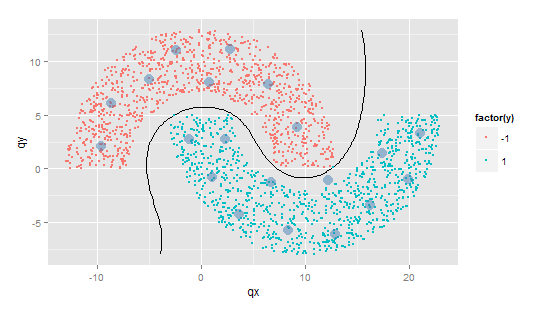
这是分类边界及各高斯隐藏单元的中心位置。界线画的比神经网络圆滑多了。

接下来试试RLS算法。
下面的代码用来取代上边的最小二乘滤波方法的那行。

n = 1 #就只迭代1轮好了。
MSE = c() #记录每次迭代后的均方差。

#初始化权值向量和矩阵P。在这里P就随便用个单位矩阵。
W = matrix(0,nrow=K)
P = diag(K)

for(t in 1:n){
  for(i in 1:N){
    pi = Phi[i,] #映射后的样本phi_i。
    #迭代计算矩阵P
    P=P-(P %*% pi %*% t(pi) %*% P)/as.numeric (1+t(pi) %*% P %*% pi)

    alpha = d[i]-t(pi)%*%W #计算先验估计误差
    W = W + P%*%pi*as.numeric(alpha) #更新权值

    MSE[i] = mean((d - Phi %*% W)**2) #计算并记录均方差。
  }
}

最终的分类误差依然只有0.05%。

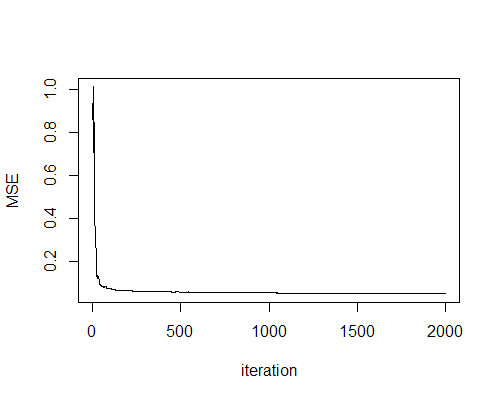
同时可知，一轮迭代在刚开始的时候就已经收敛到了一个较低的水平，RLS算法在效率上有突出优势。

R代码实验2

接着来玩一下从《机器学习实战》里借来的数据集，出处为该书附带的源码里边的第6章支持向量机部分。
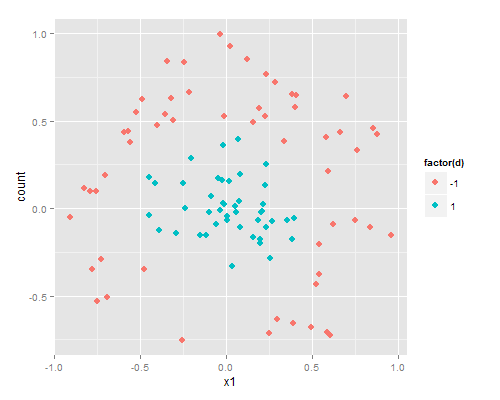
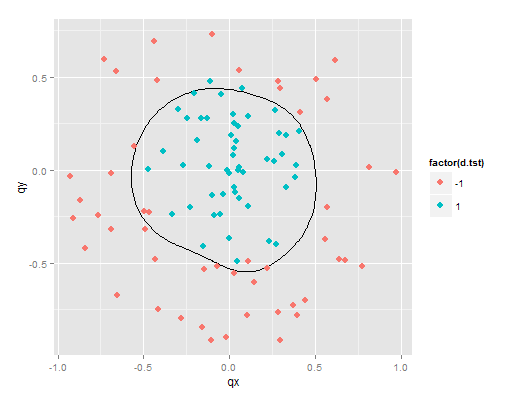
该数据集名字在这很应景，叫testSetRBF以及testSetRBF2，分别是训练集和测试集，各有分成两类的100个点。
它们画出来是酱紫的：

训练集

测试集

首先各参数保持用在双月牙数据集身上的不变先跑一趟训练集：

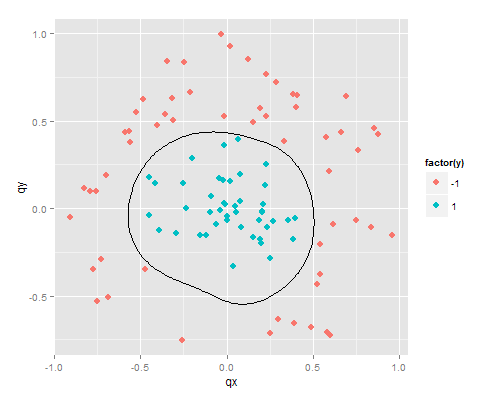
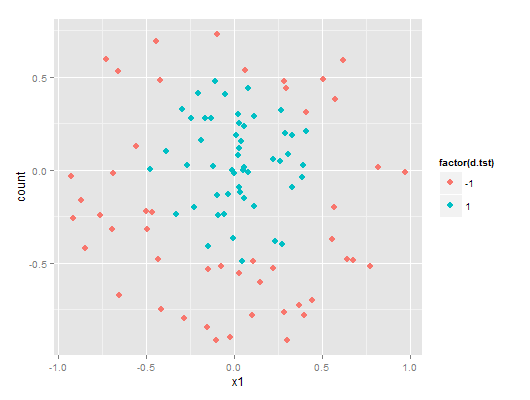
训练结果的误分类率为0。那么训练结果用在测试集上呢？

#在这里测试集的样本矩阵为X.tst，期望响应向量为d.tst
Phi.tst=t(apply(X.tst,1,function(x)apply(cnt,1,function(x1)phi(x,x1,sigma))))
y.tst= sign(Phi.tst %*% W)
length(y.tst[y.tst!=d.tst])/length(y.tst)*100

> length(y.tst[y.tst!=d.tst])/length(y.tst)*100
[1] 5

测试集中有5%的样本被误分类了。
总的来说泛化能力差强人意吧。