视觉SLAM笔记（39） 求解 ICP

---

1. SVD 方法

使用 SVD 以及非线性优化来求解 ICP
使用两个 RGB-D 图像，通过特征匹配获取两组 3D 点，最后用 ICP 计算它们的位姿变换
由于 OpenCV 目前还没有计算两组带匹配点的 ICP 的方法，而且它的原理也并不复杂
所以自己来实现一个 ICP

ICP 的实现方式和前文 视觉SLAM笔记（38） 3D-3D: ICP 讲述的是一致的

void pose_estimation_3d3d(
    const vector<Point3f>& pts1,
    const vector<Point3f>& pts2,
    Mat& R, Mat& t
)
{
    Point3f p1, p2;     // 质心
    // 计算质心位置
    int N = pts1.size();
    for (int i = 0; i < N; i++)
    {
        p1 += pts1[i];
        p2 += pts2[i];
    }
    p1 = Point3f(Vec3f(p1) / N);
    p2 = Point3f(Vec3f(p2) / N);

    // 去质心坐标
    vector<Point3f>     q1(N), q2(N); 
    for (int i = 0; i < N; i++)
    {
        q1[i] = pts1[i] - p1;
        q2[i] = pts2[i] - p2;
    }

    // 计算 q1*q2^T
    Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
    for (int i = 0; i < N; i++)
    {
        W += Eigen::Vector3d(q1[i].x, q1[i].y, q1[i].z) * Eigen::Vector3d(q2[i].x, q2[i].y, q2[i].z).transpose();
    }
    cout << "W=" << W << endl;

    // 对 W 进行 SVD 分解
    Eigen::JacobiSVD<Eigen::Matrix3d> svd(W, Eigen::ComputeFullU | Eigen::ComputeFullV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();
    cout << "U=" << U << endl;
    cout << "V=" << V << endl;

    // 计算 R, t
    Eigen::Matrix3d R_ = U * (V.transpose());
    Eigen::Vector3d t_ = Eigen::Vector3d(p1.x, p1.y, p1.z) - R_ * Eigen::Vector3d(p2.x, p2.y, p2.z);

    // 转换车矩阵cv::Mat
    R = (Mat_<double>(3, 3) <<
        R_(0, 0), R_(0, 1), R_(0, 2),
        R_(1, 0), R_(1, 1), R_(1, 2),
        R_(2, 0), R_(2, 1), R_(2, 2)
        );
    t = (Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));
}

调用 Eigen 进行 SVD，然后计算 R, t矩阵

int main(int argc, char** argv)
{
    if (argc != 5)
    {
        cout << "usage: pose_estimation_3d3d img1 img2 depth1 depth2" << endl;
        return 1;
    }
    //-- 读取图像
    Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
    Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);

    //-- 特征提取
    vector<KeyPoint> keypoints_1, keypoints_2;
    vector<DMatch> matches;
    find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
    cout << "一共找到了" << matches.size() << "组匹配点" << endl;

    // 建立3D点
    Mat depth1 = imread(argv[3], CV_LOAD_IMAGE_UNCHANGED);       // 深度图为16位无符号数，单通道图像
    Mat depth2 = imread(argv[4], CV_LOAD_IMAGE_UNCHANGED);       // 深度图为16位无符号数，单通道图像
    Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1); // 相机内参
    vector<Point3f> pts1, pts2;

    for (DMatch m : matches)
    {
        ushort d1 = depth1.ptr<unsigned short>(int(keypoints_1[m.queryIdx].pt.y))[int(keypoints_1[m.queryIdx].pt.x)];
        ushort d2 = depth2.ptr<unsigned short>(int(keypoints_2[m.trainIdx].pt.y))[int(keypoints_2[m.trainIdx].pt.x)];
        if (d1 == 0 || d2 == 0)   // bad depth
            continue;
        Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K); // 像素坐标转相机归一化坐标
        Point2d p2 = pixel2cam(keypoints_2[m.trainIdx].pt, K);
        float dd1 = float(d1) / 5000.0;
        float dd2 = float(d2) / 5000.0;
        pts1.push_back(Point3f(p1.x*dd1, p1.y*dd1, dd1));   // 添加第一个图的特征位置 3D 点
        pts2.push_back(Point3f(p2.x*dd2, p2.y*dd2, dd2));
    }

    // 3D-3D位姿估计,ICP通过SVD方法
    cout << "3d-3d pairs: " << pts1.size() << endl;
    Mat R, t;
    pose_estimation_3d3d(pts1, pts2, R, t);
    cout << "ICP via SVD results: " << endl;
    cout << "R = " << R << endl;
    cout << "t = " << t << endl;
    cout << "R_inv = " << R.t() << endl;
    cout << "t_inv = " << -R.t() *t << endl;
}

输出了匹配后的结果，不过请注意，由于前面的推导是按照 $p$_i = $Rp$_i$\prime +t$进行的
这里的 R，t 是第二帧到第一帧的变换，与前面 视觉SLAM笔记（37） 求解 PnP 部分是相反的
所以在输出结果中，同时打印了逆变换：

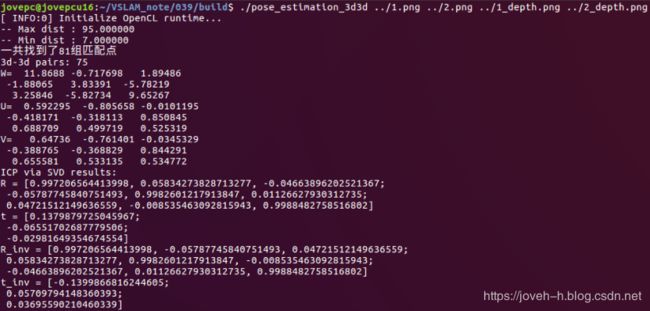
可以比较一下 ICP 与 PnP, 对极几何的运动估计结果之间的差异

可以认为，在这个过程中使用了越来越多的信息（没有深度——有一个图的深度——有两个图的深度）
因此，在深度准确的情况下，得到的估计也将越来越准确
但是，由于 Kinect 的深度图存在噪声，而且有可能存在数据丢失的情况
使得我们不得不丢弃一些没有深度数据的特征点，这可能导致 ICP 的估计不够准确
并且，如果特征点丢弃得太多，可能引起由于特征点太少，无法进行运动估计的情况

---

2. 非线性优化方法

现在用非线性优化来计算 ICP，依然使用李代数来表达相机位姿
与SVD 思路不同的地方在于，在优化中不仅考虑相机的位姿，同时会优化 3D 点的空间位置
RGB-D 相机每次可以观测到路标点的三维位置，从而产生一个 3D 观测数据
不过，由于 g2o/sba 中没有提供 3D 到 3D 的边
而又想使用 g2o/sba 中李代数实现的位姿节点
所以最好的方式是自定义一种这样的边EdgeProjectXYZRGBDPoseOnly，并向 g2o 提供解析求导方式

class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, g2o::VertexSE3Expmap>
{
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
    EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d& point) : _point(point) {}

    virtual void computeError()
    {
        const g2o::VertexSE3Expmap* pose = static_cast<const g2o::VertexSE3Expmap*> (_vertices[0]);
        // measurement is p, point is p'
        _error = _measurement - pose->estimate().map(_point);
    }

    virtual void linearizeOplus()
    {
        g2o::VertexSE3Expmap* pose = static_cast<g2o::VertexSE3Expmap *>(_vertices[0]);
        g2o::SE3Quat T(pose->estimate());
        Eigen::Vector3d xyz_trans = T.map(_point);
        double x = xyz_trans[0];
        double y = xyz_trans[1];
        double z = xyz_trans[2];

        _jacobianOplusXi(0, 0) = 0;
        _jacobianOplusXi(0, 1) = -z;
        _jacobianOplusXi(0, 2) = y;
        _jacobianOplusXi(0, 3) = -1;
        _jacobianOplusXi(0, 4) = 0;
        _jacobianOplusXi(0, 5) = 0;

        _jacobianOplusXi(1, 0) = z;
        _jacobianOplusXi(1, 1) = 0;
        _jacobianOplusXi(1, 2) = -x;
        _jacobianOplusXi(1, 3) = 0;
        _jacobianOplusXi(1, 4) = -1;
        _jacobianOplusXi(1, 5) = 0;

        _jacobianOplusXi(2, 0) = -y;
        _jacobianOplusXi(2, 1) = x;
        _jacobianOplusXi(2, 2) = 0;
        _jacobianOplusXi(2, 3) = 0;
        _jacobianOplusXi(2, 4) = 0;
        _jacobianOplusXi(2, 5) = -1;
    }

    bool read(istream& in) {}
    bool write(ostream& out) const {}
protected:
    Eigen::Vector3d _point;
};

这是一个一元边，写法类似于前面提到的 g2o::EdgeSE3ProjectXYZ
不过观测量从 2 维变成了 3 维，内部没有相机模型，并且只关联到一个节点
雅可比矩阵给出了关于相机位姿的导数，是一个3 × 6 的矩阵

调用 g2o 进行优化的代码是相似的，设定好图优化的节点和边即可
调用优化函数进行求解

// 使用 BA 优化
cout << "calling bundle adjustment" << endl;
bundleAdjustment(pts1, pts2, R, t);

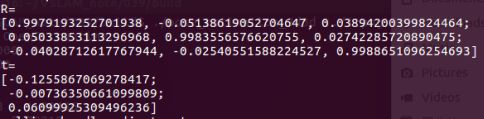
现在，来看看优化的结果：

发现只迭代一次后，总体误差就已经稳定不变，说明仅在一次迭代之后算法即已收敛
从位姿求解的结果可以看出，它和前面 SVD 给出的位姿结果几乎一模一样

这说明 SVD 已经给出了优化问题的解析解
所以，本实验中可以认为 SVD 给出的结果是相机位姿的最优值

需要说明的是，在本例的 ICP 中，使用了在两个图都有深度读数的特征点
然而，事实上，只要其中一个图深度确定，就能用类似于 PnP 的误差方式，把它们也加到优化中来
同时，除了相机位姿之外，将空间点也作为优化变量考虑，亦是一种解决问题的方式
应当清楚，实际的求解是非常灵活的，不必拘泥于某种固定的形式
如果同时考虑点和相机，整个问题就变得 更自由 了，可能会得到其他的解
比如，可以让相机少转一些角度，而把点多移动一些
这从另一侧面反映出，在 Bundle Adjustment 里面，会希望有尽可能多的约束
因为多次观测会带来更多的信息，就能够更准确地估计每个变量

---

参考：

《视觉SLAM十四讲》

---

相关推荐：

视觉SLAM笔记（38） 3D-3D: ICP
视觉SLAM笔记（37） 求解 PnP
视觉SLAM笔记（36） 3D-2D: PnP
视觉SLAM笔记（35） 三角化求特征点的空间位置
视觉SLAM笔记（34） 三角测量

---