深度学习笔记（26） 卷积神经网络

---

1. CONV

假设，有一张大小为32×32×3的输入图片，这是一张RGB模式的图片
想做手写体数字识别
32×32×3的RGB图片中含有某个数字，想识别它是从0-9这10个数字中的哪一个

用的这个网络模型和经典网络LeNet-5非常相似，灵感也来源于此
LeNet-5是Yann LeCun创建的，采用的模型并不是LeNet-5
但是受它启发，许多参数选择都与LeNet-5相似

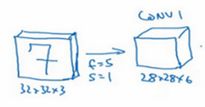
输入32×32×3
假设第一层使用过滤器大小为5×5，步幅s是1，padding是0，过滤器个数为6
则输出为28×28×6

用了6个过滤器，增加了偏差，应用了非线性函数，可能是ReLU非线性函数
最后输出CONV1的结果

---

2. POOL

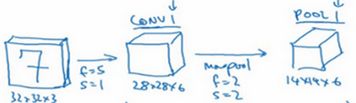
然后构建一个池化层，这里选择用最大池化，参数 f = 2，s = 2， padding = 0
现在开始构建池化层，最大池化使用的过滤器为2×2，步幅为2，表示层的高度和宽度会减少一半
因此，28×28变成了14×14，通道数量保持不变
所以最终输出为14×14×6，将该输出标记为POOL1

---

3. Layer

在卷积神经网络文献中，卷积有两种分类，这与所谓层的划分存在一致性
一类卷积是一个卷积层和一个池化层一起作为一层，这就是神经网络的Layer1
另一类卷积是把卷积层作为一层，而池化层单独作为一层
在计算神经网络有多少层时，通常只统计具有权重和参数的层
而池化层没有权重和参数，只有一些超参数

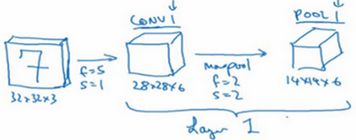
这里，把CONV1和POOL1共同作为一个卷积，并标记为Layer1

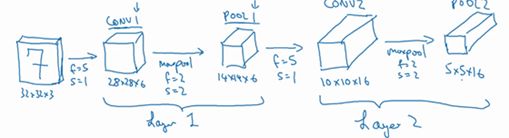
再构建一个卷积层
过滤器大小为5×5，步幅为1，这次用16个过滤器
最后输出一个10×10×16矩阵CONV2

然后做最大池化，超参数 f=2，s=2，高度和宽度会减半
输出为5×5×16 POOL2
这就是第二个卷积层，即Layer2

---

4. FC

5×5×16矩阵包含400个元素
将POOL2平整化为一个大小为400的一维向量
利用这400个单元构建下一层

下一层含有120个单元，这就是第一个全连接层，标记为FC3

它很像在讲过的单神经网络层，这是一个标准的神经网络，这400个单元与120个单元紧密相连
它的权重矩阵为W^[3] ，维度为120×400

然后对这个120个单元再添加一个全连接层，这层更小
假设它含有84个单元，标记为FC4

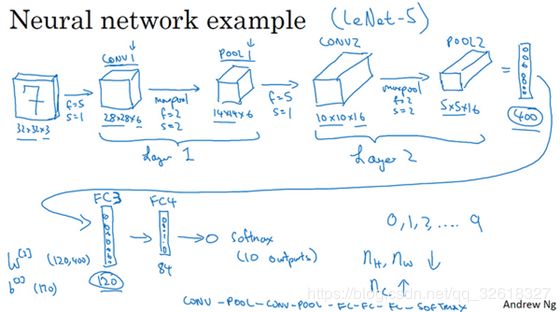
最后，用这84个单元填充一个softmax单元
如果想通过手写数字识别来识别手写0-9这10个数字
这个softmax就会有10个输出

此例中的卷积神经网络很典型，看上去它有很多超参数
常规做法是，尽量不要自己设置超参数
而是查看文献中别人采用了哪些超参数，选一个在别人任务中效果很好的架构
那么它也有可能适用于自己的应用程序

---

5. 卷积的优势

卷积层的两个主要优势在于参数共享和稀疏连接

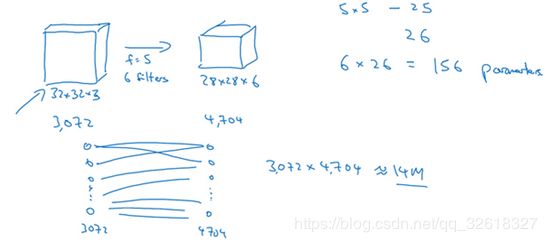
假设有一张32×32×3维度的图片
假设用了6个大小为5×5的过滤器，输出维度为28×28×6
32×32×3=3072，28×28×6=4704
构建一个神经网络
其中一层含有3072个单元，下一层含有4074个单元，两层中的每个神经元彼此相连
然后计算权重矩阵，它等于4074×3072≈1400万
所以要训练的参数很多

虽然以现在的技术，可以用1400多万个参数来训练网络
但这张32×32×3的图片非常小
如果这是一张1000×1000的图片，权重矩阵会变得非常大

这个卷积层的参数数量，每个过滤器都是5×5，一个过滤器有25个参数
再加上偏差参数，那么每个过滤器就有26个参数
一共有6个过滤器，所以参数共计156个，参数数量还是很少

卷积网络映射这么少参数有两个原因：

1. 参数共享

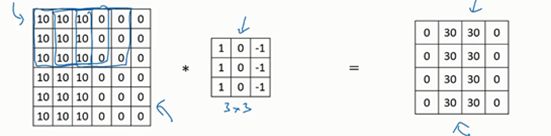
特征检测如垂直边缘检测如果适用于图片的某个区域
那么它也可能适用于图片的其他区域

也就是说，如果用一个3×3的过滤器检测垂直边缘
那么图片的左上角区域，以及旁边的各个区域也可以使用这个3×3的过滤器

每个特征检测器以及输出都可以在输入图片的不同区域中使用同样的参数
以便提取垂直边缘或其它特征
它不仅适用于边缘特征这样的低阶特征，同样适用于高阶特征
例如提取脸上的眼睛，猫或者其他特征对象

即使减少参数个数，这9个参数同样能计算出16个输出
直观感觉是，一个特征检测器
如垂直边缘检测器用于检测图片左上角区域的特征
这个特征很可能也适用于图片的右下角区域
因此在计算图片左上角和右下角区域时，不需要添加其它特征检测器

假如有一个这样的数据集，其左上角和右下角可能有不同分布，也有可能稍有不同
但很相似，整张图片共享特征检测器，提取效果也很好

2. 稀疏连接

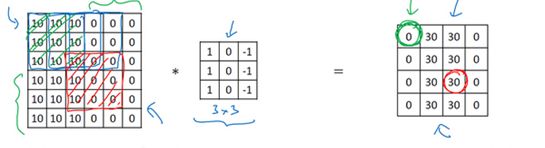
左上角这个0是通过3×3的卷积计算得到的，它只依赖于这个3×3的输入的单元格
右边这个输出单元（元素0）仅与36个输入特征中9个相连接
而且其它像素值都不会对输出产生任影响，这就是稀疏连接的概念

再举一个例子，右边矩阵中红色标记的元素 30这个输出仅仅依赖于9个特征（左边矩阵红色方框标记的区域）
看上去只有这9个输入特征与输出相连接，其它像素对输出没有任何影响

神经网络可以通过这两种机制减少参数
以便用更小的训练集来训练它，从而预防过度拟合
也可能听过，卷积神经网络善于捕捉平移不变
向右移动两个像素，图片中的猫依然清晰可见
因为神经网络的卷积结构使得即使移动几个像素
这张图片依然具有非常相似的特征，应该属于同样的输出标记

实际上，用同一个过滤器生成各层中，图片的所有像素值
希望网络通过自动学习变得更加健壮，以便更好地取得所期望的平移不变属性
这就是卷积或卷积网络在计算机视觉任务中表现良好的原因

最后，把这些层整合起来，训练这些网络，比如要构建一个猫咪检测器
有标记训练集，x表示一张图片， $\hat{y}$ 是二进制标记或某个重要标记
选定了一个卷积神经网络，输入图片，增加卷积层和池化层
然后添加全连接层，最后输出一个softmax，即 $\hat{y}$

卷积层和全连接层有不同的参数w和偏差b
可以用任何参数集合来定义代价函数，并随机初始化其参数w和b

代价函数J等于神经网络对整个训练集的预测的损失总和再除以m，即：

所以训练神经网络，要做的就是使用梯度下降法，或其它算法
例如Momentum梯度下降法
含RMSProp或其它因子的梯度下降来优化神经网络中所有参数
以减少代价函数J的值

---

参考：

《神经网络和深度学习》视频课程

---

相关推荐：

深度学习笔记（25） 池化层
深度学习笔记（24） 卷积层
深度学习笔记（23） 卷积维度
深度学习笔记（22） Padding
深度学习笔记（21） 边缘检测

---

谢谢！