最详细的Tarjan
Tarjan是一个非常牛逼的人,那么我想在这篇文章中来讲解一下他所发明的这个算法Tarjan。
一、Tarjan求强连通分量
Tarjan的主业其实是求强连通分量。但其实这个算法还是比较多能的,还可以用来缩点,判环等等,那么先看这个算法裸的模板。
想来想去还是百度最清楚。
如果两个顶点可以相互通达,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
Tarjan算法是用来求有向图的强连通分量的。求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
当DFN(u)=Low(u)时,以u为根的搜索子树上所有节点是一个强连通分量。
为了实现上面的操作,我们需要一些数组
(1)、dfn[ ],表示这个点在dfs时是第几个被搜到的。
(2)、low[ ],表示这个点以及其子孙节点连的所有点中dfn最小的值
(3)、a[ ],表示当前所有可能能构成是强连通分量的点。
(4)、flag[ ],表示一个点是否在a[ ]数组中。
那么按照之上的思路,我们来考虑这几个数组的用处以及tarjan的过程。
假设现在开始遍历点u:
(1)、首先初始化dfn[u]=low[u]=第几个被dfs到
(2)、将u存入a[ ]中,并将flag[u]设为true
(3)、遍历u的每一个能到的点,如果这个点仍未访问过,那么就对点v进行dfs,然后low[u]=min(low[u],low[v])。
(4)、假设我们已经dfs完了u的所有的子树那么之后无论我们再怎么dfs,u点的low值已经不会再变了。
对了,tarjan一遍不能搜完所有的点,因为存在孤立点或者其他
所以我们要对一趟跑下来还没有被访问到的点继续跑tarjan
怎么知道这个点有没有被访问呢?看看它的dfn是否为0!
接下来是对算法流程的演示。
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
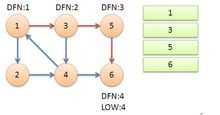
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
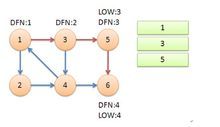
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
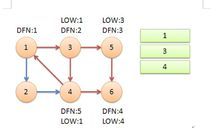
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
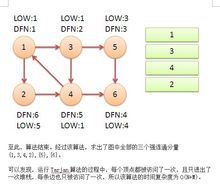
至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现,运行Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(N+M)。
来看一道模板题[USACO06JAN]牛的舞会The Cow Prom。
只要注意标记每个强连通分量的节点个数就行了。
Code:
#include
#include
#include
#define N 20005
using namespace std;
int flag[N],low[N],dfn[N],a[N],deep,top,cnt[N],color[N],sum;
vector mp[N];
int inline read()
{
int x=0,f=1;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s<='9'&&s>='0'){x=x*10+s-'0';s=getchar();}
return x*f;
}
void tarjan(int u)
{
dfn[u]=++deep;
low[u]=deep;
flag[u]=1;
a[++top]=u;
for(int i=0;i1)ans++;
printf("%d",ans);
return 0;
} 二、Tarjan缩点
我们发现某些题目中可以把一个强连通分量缩成一个点,还是看一道例题POJ2186。
对于这道题,我们可以把每个强连通分量都缩成一个点,这样图就变成了一个DAG,此时如果只有一个出度为0的点,则输出这个强连通分量所包含的点,否则输出0。
Code:
#include
#include
#include
#include
#include
#include
#include
#define N 10005
using namespace std;
int dfn[N],low[N],deep,a[N],top,flag[N],color[N],sum,cnt[N],out[N];
vector edge[N];
int inline read()
{
int x=0,f=1;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
return x*f;
}
void tarjan(int u)
{
low[u]=dfn[u]=++deep;
a[++top]=u;flag[u]=true;
for(int i=0;i1)puts("0");else printf("%d\n",ans);
return 0;
} 三、Tarjan求割点与桥
首先我们需要知道什么是割点与桥?
在一个无向图(特别注意)中,如果有一个顶点集合,删除这个顶点集合以及这个集合中所有顶点相关联的边以后,图的连通分量增多,就称这个点集为割点集合。
如果某个割点集合只含有一个顶点X(也即{X}是一个割点集合),那么X称为一个割点。(废话)
设G是一个图,v是G的一个顶点,如果G-v的连通分支数大于G的连通分支数,则称v是G的一个割点。
设G是一个图,x是G的一条边,如果G-x的连通分支数大于G的连通分支数,则称x是G的一个桥,或割边。
图中,顶点u和v都是割点,其他顶点都不是割点,边uv是桥,其他边都不是桥。
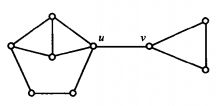
来看一道模板题洛谷3388。注意割点是在无向图中!
Code:
#include
#include
#include
#include
#include
#include
#include
#define N 100005
using namespace std;
int low[N],dfn[N],deep=0,flag[N],ans=0;
vector edge[N];
int inline read()
{
int x=0,f=1;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
return x*f;
}
void tarjan(int u,int father)
{
int son=0;
low[u]=dfn[u]=++deep;
for(int i=0;i=dfn[u])flag[u]=true;//如果这个点的子孙没有一个与它的祖先相连,那么这个点是割点。
}else if(v!=father)low[u]=min(low[u],dfn[v]);
}
if(father==-1&&son==1)flag[u]=false;//如果根节点只有一个儿子,那么根节点不是割点。
}
int main()
{
int n=read(),m=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
edge[u].push_back(v);
edge[v].push_back(u);
}
memset(dfn,0,sizeof(dfn));
memset(flag,false,sizeof(flag));
for(int i=1;i<=n;i++)
if(!dfn[i])tarjan(i,-1);
for(int i=1;i<=n;i++)if(flag[i])ans++;
printf("%d\n",ans);
for(int i=1;i<=n;i++)
if(flag[i])printf("%d ",i);
return 0;
} 下面看一道Tarjan求桥的模板题tyvj1312。其实和割点差不多。
Code:
#include
#include
#include
#include
#include
#include
#define N 10005
using namespace std;
int tot=0,head[N],deep=0,cnt=0,dfn[N],low[N];
struct edge
{
int vet,next;
}edge[N];
struct bridge
{
int start,end;
}ans[N];
bool cmp(bridge a,bridge b)
{
if(a.start!=b.start)return a.startdfn[u])
{
int from=u,to=v;
if(from>to)swap(from,to);
ans[++cnt].start=from;
ans[cnt].end=to;
}
}else if(v!=father)low[u]=min(low[u],dfn[v]);
}
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
memset(dfn,0,sizeof(dfn));
for(int i=1;i<=n;i++)
if(!dfn[i])tarjan(i,-1);
sort(ans+1,ans+cnt+1,cmp);
for(int i=1;i<=cnt;i++)
printf("%d %d\n",ans[i].start,ans[i].end);
} 四、Tarjan求双联通分量
双连通分量又分双连通分量和边双连通分量两种。若一个无向图中的去掉任意一个节点(一条边)都不会改变此图的连通性,即不存在割点(桥),则称作点(边)双连通图。一个无向图中的每一个极大点(边)双连通子图称作此无向图的点(边)双连通分量。
求点双联通分量:在求割点的过程中就能把每个点双连通分支求出。建立一个栈,存储双连通分支。在搜索图时,每找到一条树枝边或后向边(非横叉边),就把这条边加入栈中。如果遇到某时满足DFS(u)<=Low(v),说明u是一个割点,同时把边从栈顶一个个取出,直到遇到了边(u,v),取出的这些边与其关联的点,组成一个点双连通分支。最大的点双联通分支就是点双联通分量。
Code:
#include
#define N 105
using namespace std;
struct side
{
int u,v,next;
}edge[N],k;
int head[N],tot=0,deep=0,dfn[N],low[N],flag[N],color[N],cnt=0;
stackS;
vectorans[N];
void add(int u,int v)
{
edge[++tot].u=u;
edge[tot].v=v;
edge[tot].next=head[u];
head[u]=tot;
}
void tarjan(int u,int father)
{
int son=0;
dfn[u]=low[u]=++deep;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].v;
if(!dfn[v])
{
S.push(edge[i]);
son++;
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
{
flag[u]=true;
ans[++cnt].clear();
while(1)
{
k=S.top();S.pop();
if(color[k.u]!=cnt)
{
ans[cnt].push_back(k.u);
color[k.u]=cnt;
}
if(color[k.v]!=cnt)
{
ans[cnt].push_back(k.v);
color[k.v]=cnt;
}
if(k.u==edge[i].u&&k.v==edge[i].v)break;
}
}
}else
if(dfn[v]
例题:UVALive 5135。看到很多人都把每个点双联通分量求出来了,其实只要求出割点再dfs一遍就可以了。
Code:
#include
#include
#include
#include
#include
#include
#include
#define N 100005
using namespace std;
int tot,head[N],dfn[N],low[N],deep,flag[N],sum,b[N],t;
set Ans;
struct edge
{
int vet,next;
}edge[N];
void add(int u,int v)
{
edge[++tot].vet=v;
edge[tot].next=head[u];
head[u]=tot;
}
void tarjan(int u,int father)
{
int son=0;
low[u]=dfn[u]=++deep;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].vet;
if(!dfn[v])
{
son++;
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u])
flag[u]=true;
}else
if(v!=father)low[u]=min(low[u],dfn[v]);
}
if(son==1&&father==-1)flag[u]=false;
if(flag[u])sum++;
}
void dfs(int u)
{
if(flag[u]||b[u])return;
t++;
b[u]=true;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].vet;
if(flag[v])
{
Ans.insert(v);
continue;
}
dfs(v);
}
}
int main()
{
int n,m,cnt=0;
scanf("%d",&m);
while(m!=0)
{
tot=0;int n=0;
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
n=max(n,max(u,v));
add(u,v);add(v,u);
}
deep=0;sum=0;
memset(flag,false,sizeof(flag));
memset(dfn,0,sizeof(dfn));
tarjan(1,-1);
printf("Case %d: ",++cnt);
if(sum==0)
{
long long ans=n*(n-1)/2;
printf("2 %lld\n",ans);
continue;
}
memset(b,false,sizeof(b));
long long ans=1;sum=0;
for(int u=1;u<=n;u++)
if(!b[u]&&!flag[u])
{
t=0;
Ans.clear();
dfs(u);
if(Ans.size()==1&&t)
{
ans*=t;
sum++;
}
}
printf("%d %d\n",sum,ans);
scanf("%d",&m);
}
return 0;
}
求边双联通分量:非常简单,在求出所有的桥以后,把桥边删除,原图变成了多个连通块,则每个连通块就是一个边双连通分支。桥不属于任何一个边双连通分支,其余的边和每个顶点都属于且只属于一个边双连通分支。最大的边双联通分支就是边双联通分量。
看一道例题:POJ3352。
题意:一个有桥的连通图,如何把它通过加边变成边双连通图 。
首先求出所有的桥,然后删除这些桥边,剩下的每个连通块都是一个双连通子图。把每个双连通子图收缩为一个顶点,再把桥边加回来,最后的这个图一定是一棵树,边连通度为1。
统计出树中度为1的节点的个数,记为leaf。则至少在树上添加(leaf+1)/2条边,就能使树达到边双连通,所以至少添加的边数就是(leaf+1)/2。
Code:
#include
#include
#include
#include
#include
#include
#define N 1005
using namespace std;
int tot=0,p=0,color[N],b[N],head[N*2],deep=0;
int cnt=0,dfn[N],out[N],low[N],mp[N][N];
struct edge
{
int vet,next;
}edge[N*2];
struct bridge
{
int start,end;
}ans[N*2];
void add(int u,int v)
{
edge[++tot].vet=v;
edge[tot].next=head[u];
head[u]=tot;
}
void tarjan(int u,int father)
{
dfn[u]=low[u]=++deep;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].vet;
if(!dfn[v])
{
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>dfn[u])
{
ans[++cnt].start=u;
ans[cnt].end=v;
}
}else if(v!=father&&dfn[v] 这是最易懂的写法,这个写法可以处理出所以的边或点,但其实有更简单的写法直接处理出点。
Code:
#include
#include
#include
#include
#include
#include
#define N 1005
using namespace std;
int tot=0,p=0,color[N],b[N],head[N*2],deep=0,top=0;
int cnt=0,dfn[N],out[N],low[N],mp[N][N],s[N*2];
struct edge
{
int vet,next;
}edge[N*2];
void add(int u,int v)
{
edge[++tot].vet=v;
edge[tot].next=head[u];
head[u]=tot;
}
void tarjan(int u,int father)
{
dfn[u]=low[u]=++deep;
s[++top]=u;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].vet;
if(!dfn[v])
{
tarjan(v,u);
low[u]=min(low[u],low[v]);
}else if(v!=father)
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])//当dfs序和low相等时说明当前u在桥的末端,那么栈中的top到u所在的位置的点都在同一个双联通分量中
{
p++;
while(s[top]!=u&&top)
{
color[s[top]]=p;
top--;
}
color[s[top--]]=p;
}
}
void dfs(int u)
{
color[u]=p;
b[u]=false;
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].vet;
if(b[v]&&mp[u][v])dfs(v);
}
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(color,0,sizeof(color));
for(int i=1;i<=n;i++)
if(!dfn[i])tarjan(i,-1);
for(int u=1;u<=n;u++)
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].vet;
if(color[u]!=color[v])
{
out[color[u]]++;
out[color[v]]++;
}
}
int ans=0;
for(int i=1;i<=p;i++)
if(out[i]/2==1)ans++;
printf("%d\n",(ans+1)/2);
return 0;
}