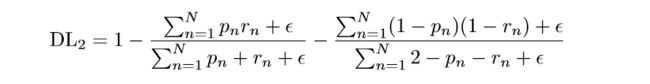Dice loss
转自:咖啡味儿的咖啡
https://blog.csdn.net/wangdongwei0/article/details/84576044
Dice Loss
首先定义两个轮廓区域的相似程度,用A、B表示两个轮廓区域所包含的点集,定义为:
![]()
那么loss为:
可以看出,Dice Loss其实也可以分为两个部分,一个是前景的loss,一个是物体的loss,但是在实现中,我们往往只关心物体的loss,Keras的实现如下:
-
def dice_coef(y_true, y_pred, smooth=1):
-
intersection = K.sum(y_true * y_pred, axis=[
1,
2,
3])
-
union = K.sum(y_true, axis=[
1,
2,
3]) + K.sum(y_pred, axis=[
1,
2,
3])
-
return K.mean( (
2. * intersection + smooth) / (union + smooth), axis=
0)
-
def dice_coef_loss(y_true, y_pred):
-
1 - dice_coef(y_true, y_pred, smooth=
1)
上面的代码只是实现了2分类的dice loss,那么多分类的dice loss又应该是什么样的呢?
注:正确性还没验证。。。
-
# y_true and y_pred should be one-hot
-
# y_true.shape = (None,Width,Height,Channel)
-
# y_pred.shape = (None,Width,Height,Channel)
-
def dice_coef(y_true, y_pred, smooth=1):
-
mean_loss =
0;
-
for i
in range(y_pred.shape(
-1)):
-
intersection = K.sum(y_true[:,:,:,i] * y_pred[:,:,:,i], axis=[
1,
2,
3])
-
union = K.sum(y_true[:,:,:,i], axis=[
1,
2,
3]) + K.sum(y_pred[:,:,:,i], axis=[
1,
2,
3])
-
mean_loss += (
2. * intersection + smooth) / (union + smooth)
-
return K.mean(mean_loss, axis=
0)
-
def dice_coef_loss(y_true, y_pred):
-
1 - dice_coef(y_true, y_pred, smooth=
1)