各种排序算法、十大排序算法
目录
二分查找
冒泡排序
选择排序
插入排序
希尔排序
归并排序
快速排序
堆排序
计数排序
桶排序
基数排序
外部排序与归并排序(强调一种思想)
动态规划要点:
二分查找
//不使用递归实现:while循环,时间O(log2 N),空间O(1)
public static int commonBinarySearch(int[] arr,int key){
int low = 0;
int high = arr.length - 1;
int middle = 0; //定义middle
if(key < arr[low] || key > arr[high] || low > high){
return -1;
}
while(low <= high){
middle = (low + high) / 2;
if(arr[middle] > key){
//比关键字大则关键字在左区域
high = middle - 1;
}else if(arr[middle] < key){
//比关键字小则关键字在右区域
low = middle + 1;
}else{
return middle;
}
}
return -1; //最后仍然没有找到,则返回-1
}
//使用递归实现,时间O(log2 N),空间O(log2N )
public static int recursionBinarySearch(int[] arr,int key,int low,int high){
if(key < arr[low] || key > arr[high] || low > high){
return -1;
}
int middle = (low + high) / 2; //初始中间位置
if(arr[middle] > key){
//比关键字大则关键字在左区域
return recursionBinarySearch(arr, key, low, middle - 1);
}else if(arr[middle] < key){
//比关键字小则关键字在右区域
return recursionBinarySearch(arr, key, middle + 1, high);
}else {
return middle;
}
}
二分查找优化:
1、插值查找算法
将mid=left + (right-left)/2 的计算更改为 mid = left + ((target-min)/(max-target))*(right-left),即更换1/2系数
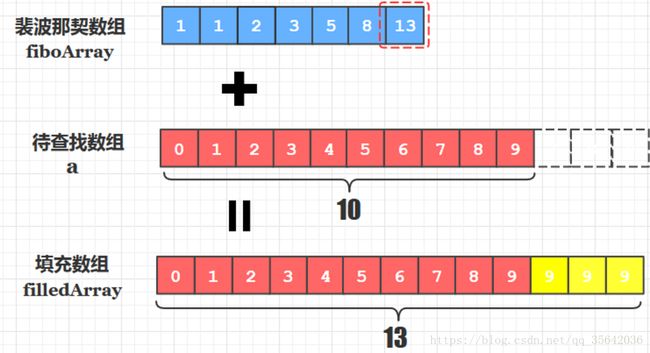
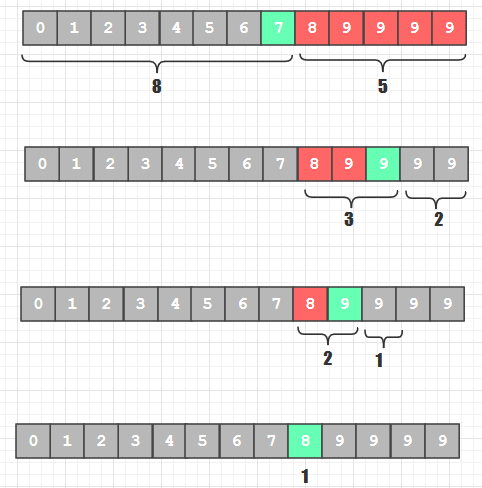
2、斐波那契查找算法
- 根据待查找数组长度确定裴波那契数组的长度(或最大元素值)
- 根据1中长度创建该长度的裴波那契数组,再通过F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)生成裴波那契数列为数组赋值
- 以2中的裴波那契数组的最大值为长度创建填充数组,将原待排序数组元素拷贝到填充数组中来, 如果有剩余的未赋值元素, 用原待排序数组的最后一个元素值填充
- 针对填充数组进行关键字查找, 查找成功后记得判断该元素是否来源于后来填充的那部分元素
参考链接:https://www.cnblogs.com/penghuwan/p/8021809.html#_label3
冒泡排序
public static void bubbleSort(int[] data){
if(data == null) return;
for (int i = 0; i < data.length; i++) {
for (int j = 1; j < data.length-i; j++) {
if (data[j-1]>data[j]) {
int temp = data[j];
data[j]=data[j-1];
data[j-1]=temp;
}
}
}
return;
}
优化版:解释链接:https://mp.weixin.qq.com/s/wO11PDZSM5pQ0DfbQjKRQA
public static void bubbleSortUpdate(int[] data){
if(data == null) return;
//记录最后一次交换的位置
int lastExchangeIndex =0; //解决原数组中后部分都为有序情况下的比较浪费
//无序数列的边界,每次比较只需要比到这里为止
int sortBorder = data.length;
for (int i = 0; i < data.length; i++) {
//有序标记,每一轮的初始是true,当有一轮比较没有找到需要更换位置的数据时,可以直接退出整个循环了
boolean isSorted = true;
for (int j = 1; j < sortBorder; j++) {
if (data[j-1]>data[j]) {
int temp = data[j];
data[j]=data[j-1];
data[j-1]=temp;
//有元素交换,所以不是有序,标记变为false
isSorted = false;
//把无序数列的边界更新为最后一次交换元素的位置
lastExchangeIndex = j;
}
}
sortBorder = lastExchangeIndex;
if (isSorted)
break;
}
return;
}
选择排序
public static void selectionSort(int[] data){
if(data == null) return;
int curMinIndex = 0;
for (int i = 0; i < data.length; i++) {
curMinIndex=i;
for (int j = i; j < data.length; j++) {
if (data[curMinIndex]>data[j]) {
curMinIndex = j;
}
}
int temp = data[i];
data[i]=data[curMinIndex];
data[curMinIndex]=temp;
}
}
插入排序
public static void insertionSort(int[] data){
if(data == null) return;
int now = 0;
int index = 0;
for (int i = 1; i < data.length; i++) {
index = i;
now = data[i];
while (index>0&&data[index-1]>now) {
data[index]=data[index-1];
index--;
}
data[index] = now;
}
}
希尔排序
public static void shellSort(int[] data){
if(data==null || data.length<=1)
return;
//数组长12 d=6 d=3
for(int gap=data.length/2; gap>0; gap=gap/2){
//i=6 7 / 3 4 5
for(int i=gap;i=0 && data[cur-gap]>temp) {
data[cur] = data[cur-gap];
cur = cur-gap;
}
data[cur]=temp;
}
}
}
归并排序
public static void Merge(int[] data){
if (data==null) return;
//在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
int[] temp = new int[data.length];
sort(data,0,data.length-1,temp);
}
private static void sort(int[] data, int start, int end, int[] temp) {
if(start
快速排序
public static void quickSort(int[] data,int start,int end) {
if (data==null) return;
if (start>=end) return;
//获得start元素在原数组中排序后的准确的位置索引
int index = partition3(data,start,end);
quickSort(data,start,index-1);
quickSort(data,index+1,end);
}
//作用:根据输入data【】,start与end,返回data[start]在排序数组中准确的位置
private static int partition(int[] data, int start, int end) {
if(start>=end)
return end;
//存储目标值
int target=data[start];
//start是前面的哨兵,end是后面的哨兵
while(end>start){
//右哨兵从当前位置循环找到一个小于目标值的index
while (end>start&&data[end]>target)
end--;
//执行与左哨兵更换,并让左哨兵走一步
if (end>start)
data[start++] = data[end];
//左哨兵循环找到一个大于目标值的index
while(end>start&&data[start]start)
data[end--] = data[start];
}
//当执行到这里,start=end
data[start]=target;
//System.out.println(start);
return start;
}
堆排序
private static void heapSort(int[] data){
if (data==null) return;
//1.构建初始大顶堆
//data.length/2-1定位到倒数第一个非叶子结点
for (int i = data.length/2-1; i >= 0; i--) {
adjustHeap(data,i,data.length);
}
//2.交换堆顶元素和末尾元素并重建堆
for (int j = data.length-1; j >0; j--) {
swapUtil.swap(data, 0, j);
adjustHeap(data,0,j);
}
}
//调整堆为最大堆,第二个参数i为需要考虑调整的节点,此处需要传入第三个参数长度,因为最后搭建排序数组的时候参加运算的数组长度会减小
private static void adjustHeap(int[] data, int i, int length) {
int temp = data[i];
for (int j = 2*i+1; j < length; j=2*j+1) {
//若当前节点的右子节点的值大于左子节点的值,则定位到右子节点
if (j+1 < length && data[j+1]>data[j]) {//若为最小堆,则第二个>换为<号
j++;
}
//若当前考虑的节点(子节点)大于其父节点,则将其赋值给父节点,不用进行交换,到退出循环时再交换
if (data[j]>temp) {//若为最小堆,则这里换为<号
data[i] = data[j];
i = j;
}else {
break;
}
}
data[i]=temp;
}
计数排序
https://mp.weixin.qq.com/s/WGqndkwLlzyVOHOdGK7X4Q(建议阅读链接!优化稳定版计数排序不在下文中)
适用于数据比较集中的情况,有一定范围,且范围不是很大(此种情况性能比ologn快)
如:20个随机整数,【0,10】,用最快的速度排序
先前的排序算法都是基于元素比较,而计数排序是利用数组下标来确定元素的正确位置
思路:根据整数的最大值max与最小值min之差dis,建立长度为dis的数组,然后遍历数组将每个数放在【数组-min】对应的位置
时间复杂度o(n+k=遍历n查找最大最小值,创建计数数组(max-min=k),再遍历n计数每个值出现的次数,再遍历新数组k进行排序)
空间复杂度o(k=max-min,创建长度为k的数组用于计数值出现的次数)
注意,以下情况不适用:
1.当数列最大最小值差距过大时,并不适用计数排序。
比如给定20个随机整数,范围在0到1亿之间,这时候如果使用计数排序,需要创建长度1亿的数组。不但严重浪费空间,而且时间复杂度也随之升高。
2.当数列元素不是整数,并不适用计数排序。
如果数列中的元素都是小数,比如25.213,或是0.00000001这样子,则无法创建对应的统计数组。这样显然无法进行计数排序。
对于这些局限性,另一种线性时间排序算法(桶排序)做出了弥补
private static void CountSort(int[] data){
if (data==null) return;
int min = data[0];
int max = data[0];
for (int i = 0; i < data.length; i++) {
if (data[i]>max) {
max = data[i];
}else if (data[i]
桶排序
适用于最大最小值相差较大的情况,但是值的分布要够均匀
时间复杂度o(n+k=遍历原数组n找到最大最小值,创建桶数组,遍历原数组n将数据放入桶,排序每个桶内元素后遍历桶取出数据k)
空间复杂度o(n+k=需要一个长度为n的数组作为桶,每个桶里面存储一个数组List,数组的每个位置区间大小为k,k=(max-min)/n+1(经过验证,这个k最好要加1,使得程序鲁棒性得以提升,即区间算出来后要加1))
public static void bucketSort(int[] arr){
//新建一个大小为原数组长度的数组
ArrayList> bucketArr = new ArrayList<>(arr.length);
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
bucketArr.add(new ArrayList());
}
//每个桶的区间大小
int bucketNum = (max - min) / arr.length+1;
//将每个元素放入桶
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / bucketNum ;
bucketArr.get(num).add(arr[i]);
}
//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
System.out.println(bucketArr.toString());
}
基数排序
时间复杂度o(n*k=遍历原数组n得到数组的最大值的位数k,再遍历k遍原数组n)
public static void radixSort(int[] a) {
int exp; // 指数。当对数组按个位进行排序时,exp=1;按十位进行排序时,exp=10;...
int max = getMax(a); // 数组a中的最大值
// 从个位开始,对数组a按"指数"进行排序
for (exp = 1; max/exp > 0; exp *= 10)
countSort2(a, exp);
}
private static void countSort2(int[] a, int exp) {
int[] output = new int[a.length]; // 存储"被排序数据"的临时数组
LinkedList[] buckets = new LinkedList[10];
for (int i = 0; i < buckets.length; i++) {
buckets[i]=new LinkedList();
}
// 将数据存储在buckets[]中
for (int i = 0; i < a.length; i++){
//int temp = (a[i]/exp)%10;
buckets[(a[i]/exp)%10].offer(a[i]);
}
int temp = 0;
// 将数据存储到临时数组output[]中
for (int j = 0; j < 10; j++) {
while (buckets[j].peek()!=null) {
output[temp++]=(int) buckets[j].poll();
}
}
// 将排序好的数据赋值给a[]
for (int i = 0; i < a.length; i++)
a[i] = output[i];
output = null;
buckets = null;
}
外部排序与归并排序(强调一种思想)
有时,待排序的文件很大,计算机内存不能容纳整个文件,这时候对文件就不能使用内部排序了(这里做一下说明,其实所有的排序都是在内存中做的,这里说的内部排序是指待排序的内容在内存中就可以完成,而外部排序是指待排序的内容不能在内存中一下子完成,它需要做内外存的内容交换),外部排序常采用的排序方法也是归并排序,这种归并方法由两个不同的阶段组成:
1、采用适当的内部排序方法对输入文件的每个片段进行排序,将排好序的片段(成为归并段)写到外部存储器中(通常由一个可用的磁盘作为临时缓冲区),这样临时缓冲区中的每个归并段的内容是有序的。
2、利用归并算法,归并第一阶段生成的归并段,直到只剩下一个归并段为止。
例如要对外存中4500个记录进行归并,而内存大小只能容纳750个记录,在第一阶段,我们可以每次读取750个记录进行排序,这样可以分六次读取,进行排序,可以得到六个有序的归并段,如下图:
每个归并段的大小是750个记录,记住,这些归并段已经全部写到临时缓冲区(由一个可用的磁盘充当)内了,这是第一步的排序结果。
完成第二步该怎么做呢?这时候归并算法就有用处了,算法描述如下:
1、将内存空间划分为三份,每份大小250个记录,其中两个用作输入缓冲区,另外一个用作输出缓冲区。首先对Segment_1和Segment_2进行归并,先从每个归并段中读取250个记录到输入缓冲区,对其归并,归并结果放到输出缓冲区,当输出缓冲区满后,将其写到临时缓冲区内,如果某个输入缓冲区空了,则从相应的归并段中再读取250个记录进行继续归并,反复以上步骤,直至Segment_1和Segment_2全都排好序,形成一个大小为1500的记录,然后对Segment_3和Segment_4、Segment_5和Segment_6进行同样的操作。
2、对归并好的大小为1500的记录进行如同步骤1一样的操作,进行继续排序,直至最后形成大小为4500的归并段,至此,排序结束。
以上对外部排序如何使用归并算法进行排序进行了简要总结,提高外部排序需要考虑以下问题:
1、如何减少排序所需的归并趟数。
2、如果高效利用程序缓冲区,使得输入、输出和CPU运行尽可能地重叠。
3、如何生成初始归并段(Segment)和如何对归并段进行归并。
此算法适用于用小内存排序大数据量的问题
假设要对1000G数据用2G内存进行排序
方法:每次把2G数据从文件传入内存,用一个“内存排序”算法排好序后,再写入外部磁盘的一个2G的文件中,之后再从1000G中载入第二个2G数据。循环500遍。就得到500个文件,每个文件2G,文件内部都是有序的。
然后进行归并排序,比较第1/500和2/500的文件,分别读入750MB进入内存,内存剩下的500MB用来临时存储生成的数据,直到将两个2G文件合并成4G,再进行后面两个2G文件的归并……。另外,也可以用归并排序的思想同时对500个2G的文件直接进行归并
优化思路:
- 增设一个缓冲buffer,加速从文件到内存的转储
假设这个buffer已经由系统帮我们优化了
- 使用流水线的工作方式,假设从磁盘读数据到内存为L,内存排序为S,排完写磁盘为T,因为L和S都是IO操作,比较耗时间,所以可以用流水线,在IO操作的同时内存也在进行排序
- 以上流水线可能会出现内存溢出的问题,所以需要把内存分为3部分。即每个流水线持有2G/3的内存。
- 在归并排序上进行优化,最后得到的500个2G文件,每次扫描文件头找最小值,最差情况要比较500次,平均时间复杂度是O(n),n为最后得到的有序数组的个数,优化思路是:维护一个大小为n的“最小堆”,每次返回堆顶元素(当前文件头数值最小的那个值),判断弹出的最小值是属于哪个文件的,将哪个文件此时的头文件所指向的数再插入最小堆中,文件指针自动后移,插入过程为logn,最小堆返回最小值为o(1),运行时空间复杂度为o(n)
参考链接:https://www.cnblogs.com/codeMedita/p/7425291.html
动态规划要点:
将原问题拆解成若干子问题,同时保存子问题的答案,使得每个子问题只求解一次,最终获得原问题的答案
大多数动态规划问题本质都是递归问题——重叠子问题——记忆化搜索(自顶向下)
——动态规划(自底向上)
- 求一个问题的最优解
- 整体问题的最优解依赖各个子问题的最优解
- 子问题之间有相互重叠的更小的子问题
- 从上往下分析问题,从下往上求解问题
三个重要概念:最优子结构,边界,状态转移公式
递归:记忆化搜索——自上而下的解决问题
动态规划——自下而上的解决问题
0-1背包问题示例:
public int SingleArray() {
int[] weight = {3,5,2,6,4}; //物品重量
int[] val = {4,4,3,5,3}; //物品价值
int length = weight.length;
int w = 12;
//如果是不需要装满,则初始化0,要装满则初始化Integer.MIN_VALUE
int[] dp = new int[w+1];//+1的目的使得i位置代表体积为i
for (int i = 0; i < length; i++) {
//for(int j=weight[i];j= weight[i] ; j--) {
dp[j] = Math.max(dp[j],dp[j-weight[i]]+val[i]);
}
}
return dp[w];
}
0-1背包问题更详细的参考链接:https://blog.csdn.net/ls5718/article/details/52227908