关于卷积神经网络（CNN）与递归/循环神经网络(RNN)的入门学习

最近科研看了两篇论文，上面分别用了两种方法，一种是卷积神经网络，另一种则是递归神经网络，因为之前没有接触过神经网络这一块知识，故特地整理一下，方便自己了解。

卷积神经网络（CNN）

卷积神经网络（Convolutional Neural Network）简称CNN，CNN是所有深度学习课程、书籍必教的模型，CNN在影像识别方面的为例特别强大，许多影像识别的模型也都是以CNN的架构为基础去做延伸。另外值得一提的是CNN模型也是少数参考人的大脑视觉组织来建立的深度学习模型，学会CNN之后，对于学习其他深度学习的模型也很有帮助，本文主要讲述了CNN的原理。

从上面一张图片我们可以看出，CNN架构简单来说就是：图片经过各两次的Convolution, Pooling, Fully Connected就是CNN的架构了，因此只要搞懂Convolution, Pooling, Fully Connected三个部分的内容就可以完全掌握了CNN！

1.1 Convolution Layer卷积层

（卷积层提取形状特征）
卷积运算就是将原始图片的与特定的Feature Detector(filter)做卷积运算(符号⊗)，卷积运算就是将下图两个3x3的矩阵作相乘后再相加，以下图为例,有$0\ast 0+0\ast 0+0\ast 1+0\ast 1+1\ast 0+0\ast 0+0\ast 0+0\ast 1+0\ast 1=0$

每次移动一步，我们可以一次做完整张表的计算，如下：

下面的动图更好地解释了计算过程：

中间的Feature Detector(Filter)（就是做卷积运算的矩阵）会随机产生好几种(ex:16种)，Feature Detector的目的就是帮助我们萃取出图片当中的一些特征(ex:形状)，就像人的大脑在判断这个图片是什么东西也是根据形状来推测 ：

利用Feature Detector萃取出物体的边界

使用Relu函数去掉负值，更能淬炼出物体的形状

去掉负值前

去掉负值后

我们在输入上进行了多次卷积，其中每个操作使用不同的过滤器（卷积×不同的矩阵）。这导致不同的特征映射。最后，我们将所有这些特征图放在一起，作为卷积层的最终输出。

就像任何其他神经网络一样，我们使用激活函数使输出非线性。在卷积神经网络的情况下，卷积的输出将通过激活函数。这可能是ReLU激活功能：

这里还有一个概念就是步长，Stride是每次卷积滤波器移动的步长。步幅大小通常为1，意味着滤镜逐个像素地滑动。通过增加步幅大小，您的滤波器在输入上滑动的间隔更大，因此单元之间的重叠更少。下面的动画显示步幅大小为1。

由于feature map的大小始终小于输入，我们必须做一些事情来防止我们的要素图缩小。这是我们使用填充的地方。

添加一层零值像素以使用零环绕输入，这样我们的要素图就不会缩小。除了在执行卷积后保持空间大小不变，填充还可以提高性能并确保内核和步幅大小适合输入。

可视化卷积层的一种好方法如下所示，最后我们以一张动图解释下卷积层到底做了什么

1.2 Pooling Layer 池化层

（池化层降低维数，减少网络中的参数和计算次数）
在卷积层之后，通常在CNN层之间添加池化层。池化的功能是不断降低维数，以减少网络中的参数和计算次数。这缩短了训练时间并控制过度拟合。

最常见的池类型是max pooling，它在每个窗口中占用最大值。需要事先指定这些窗口大小。这会降低特征图的大小，同时保留重要信息。

Max Pooling主要的好处是当图片整个平移几个Pixel的话对判断上完全不会造成影响，以及有很好的抗杂讯功能

1.3 Fully Connected Layer 全连接层

基本上全连接层的部分就是将之前的结果平坦化之后接到最基本的神经网络了

上图，从左往右，从上到下展开为列向量

1.4实践补充

待更新

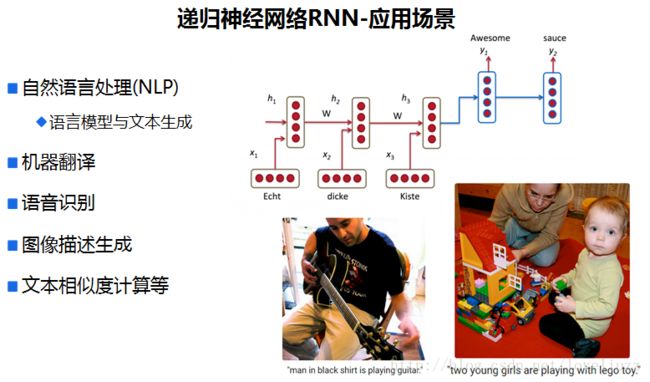
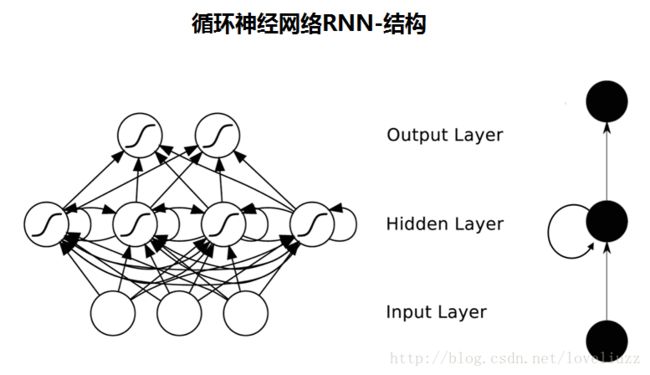
递归神经网络（RNN）

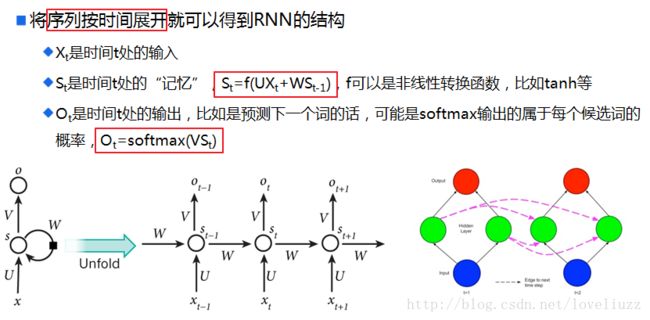
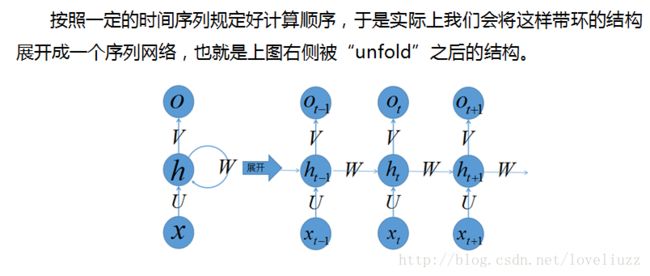
因为神经网络的输入层单元个数是固定的，因此必须用循环或者递归的方式来处理长度可变的输入。循环神经网络实现了前者，通过将长度不定的输入分割为等长度的小块，然后再依次的输入到网络中，从而实现了神经网络对变长输入的处理。一个典型的例子是，当我们处理一句话的时候，我们可以把一句话看作是词组成的序列，然后，每次向循环神经网络输入一个词，如此循环直至整句话输入完毕，循环神经网络将产生对应的输出。如此，我们就能处理任意长度的句子了。入下图所示：

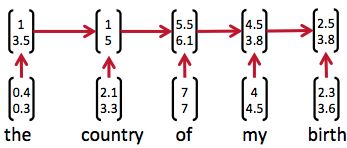
然而，有时候把句子看做是词的序列是不够的，比如下面这句话『两个外语学院的学生』：

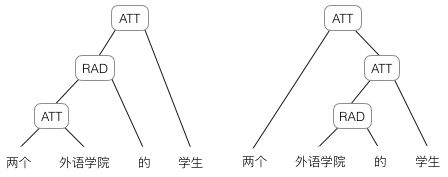
上图显示了这句话的两个不同的语法解析树。可以看出来这句话有歧义，不同的语法解析树则对应了不同的意思。一个是『两个外语学院的/学生』，也就是学生可能有许多，但他们来自于两所外语学校；另一个是『两个/外语学院的学生』，也就是只有两个学生，他们是外语学院的。为了能够让模型区分出两个不同的意思，我们的模型必须能够按照树结构去处理信息，而不是序列，这就是递归神经网络的作用。当面对按照树/图结构处理信息更有效的任务时，递归神经网络通常都会获得不错的结果。

递归神经网络可以把一个树/图结构信息编码为一个向量，也就是把信息映射到一个语义向量空间中。这个语义向量空间满足某类性质，比如语义相似的向量距离更近。也就是说，如果两句话（尽管内容不同）它的意思是相似的，那么把它们分别编码后的两个向量的距离也相近；反之，如果两句话的意思截然不同，那么编码后向量的距离则很远。如下图所示：

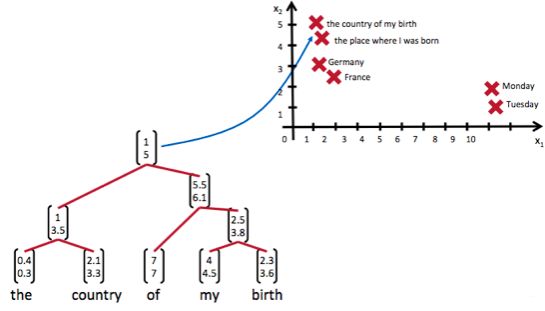
从上图我们可以看到，递归神经网络将所有的词、句都映射到一个2维向量空间中。句子『the country of my birth』和句子『the place where I was born』的意思是非常接近的，所以表示它们的两个向量在向量空间中的距离很近。另外两个词『Germany』和『France』因为表示的都是地点，它们的向量与上面两句话的向量的距离，就比另外两个表示时间的词『Monday』和『Tuesday』的向量的距离近得多。这样，通过向量的距离，就得到了一种语义的表示。

上图还显示了自然语言可组合的性质：词可以组成句、句可以组成段落、段落可以组成篇章，而更高层的语义取决于底层的语义以及它们的组合方式。递归神经网络是一种表示学习，它可以将词、句、段、篇按照他们的语义映射到同一个向量空间中，也就是把可组合（树/图结构）的信息表示为一个个有意义的向量。比如上面这个例子，递归神经网络把句子"the country of my birth"表示为二维向量[1,5]。有了这个『编码器』之后，我们就可以以这些有意义的向量为基础去完成更高级的任务（比如情感分析等）。如下图所示，递归神经网络在做情感分析时，可以比较好的处理否定句，这是胜过其他一些模型的：

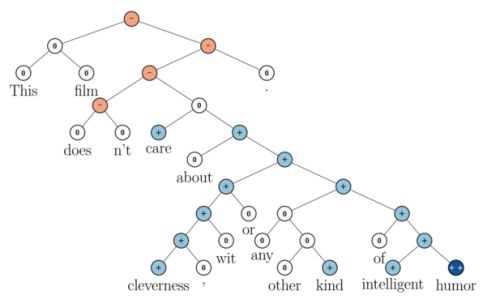
在上图中，蓝色表示正面评价，红色表示负面评价。每个节点是一个向量，这个向量表达了以它为根的子树的情感评价。比如"intelligent humor"是正面评价，而"care about cleverness wit or any other kind of intelligent humor"是中性评价。我们可以看到，模型能够正确的处理doesn’t的含义，将正面评价转变为负面评价。
尽管递归神经网络具有更为强大的表示能力，但是在实际应用中并不太流行。其中一个主要原因是，递归神经网络的输入是树/图结构，而这种结构需要花费很多人工去标注。想象一下，如果我们用循环神经网络处理句子，那么我们可以直接把句子作为输入。然而，如果我们用递归神经网络处理句子，我们就必须把每个句子标注为语法解析树的形式，这无疑要花费非常大的精力。很多时候，相对于递归神经网络能够带来的性能提升，这个投入是不太划算的。

2.3 循环神经网络的前向传播与反向传播

（一）RNN前向传播



（二）RNN反向传播