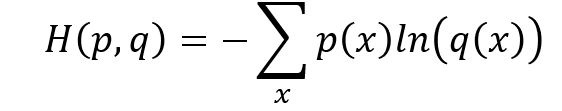softmax cross entropy loss 与 sigmoid cross entropy loss的区别

要了解两者的区别，当然要先知道什么是softmax, sigmoid, 和 cross entropy(交叉熵)了：

1、softmax:

图片来源：李宏毅机器学习课程

sotfmax其实很简单，就是输入通过一个函数映射到0-1之间的输出，上图中蓝色区域可以看做一个函数f，则有y=f(z)，（大家仔细看这个公式哇，z 和 y可我可都加粗了，所以这两个值可不是标量，而是向量，换句话说，扔进softmax一组向量，吐出也是同维度的一组向量）然后这些输出值就有概率的意义了（加起来等于1），为什么要这么做呢，一方面相当于是对输入做了一个归一化处理，另一方面，神经网络的输出要有物理意义才行，而概率是多么有意义的一个值啊。当然，为什么叫softmax呢？输出是概率呀，不是hard（硬的1），而都是一些小于1的数，当然就很soft（软）了。

比较重要的是softmax一般用于多分类的任务（因为上面说了，扔进去的一组向量嘛），比如大家熟悉的mnist数据集分类（不了解mnist的童鞋应该不多吧），要把0-9分开来，最后的输出就是接了一个softmax。关于这个等会再讲。

2、sigmoid 

sigmoid函数又叫s曲线，又叫logistic函数（名字真多）

上图！

图片来源：同上

sigmoid一般用于二分类问题（这个大家都知道）， 看上图的这个公式就知道，扔进sigmoid的是一个标量，然后吐出一个标量。也就是说只是对一个量把它映射到（0,1），于是也就具有了概率意义。当然，当softmax的输入退化为一个标量时，softmax和sigmoid在形式上就一样了。

3、cross entropy

交叉熵：要不咱们直接上公式吧（不想打公式，懒是原罪）

图片来源：同上 

这是最原始的交叉熵公式，对于这个公式，我就稍微说几句吧: 首先，要知道熵这个概念，熵是信息论里面一个概念，用来衡量信息的不确定性，信息的不确定性越大，熵就越大。那么信息的不确定性跟什么有关系呢？答案果断是概率啊。ok，所以熵的公式里有概率（没毛病）。那么交叉的意思就是需要两样东西，不然怎么交叉？所以在这里两样东西就是两个不同的概率分布p和q，交叉熵就是来衡量这两个概率分布的相似情况。我们的目标是让值两个概率分布越接近越好（想一想是不是？一个是标签label，另一个则是网络的输出）假设q是真实的标签，p是网络的输出，我们通过cross entropy loss 和BP算法（误差反向传播）来让p越来越接近q，即在完全知道q的信息量的情况下去不断的窥探q分布的信息量，慢慢的，我们也知道了q分布到底是个什么东西，这个时候两者的交叉熵就很小了，q的不确定性没剩下多少了。（可怜我q，被人家刨了祖坟。）

 

接下来，就让它们产生化学反应吧

当sotfmax 遇到cross entropy

还记得mnist吗，mnist的label是什么呢？答：是用one-hot编码的一组向量哇

0-9的编码（label）如下（哎，还是自己打公式了）： 

 再贴一波公式：

上图第一个公式就是softmax，其中x是样本，k表示类别，再想想上面说的，softmax是用于多分类，每次扔进去的是一个向量。在mnist的例子中每一个样本都是用10维向量来表示的，10维向量的每一维都不独立吧，并且是one-hot编码，只有一维是1，其他维度都是0，完美的匹配了sotfmax输入的要求。所以每次扔进sotfmax的是表示某一个数字的向量哟。

再看第二个公式，把第一个公式带入交叉熵的原始形式就可以得到这个公式，N表示mini-batch的样本数，p就是第一个公式的那个p，one-hot 编码的label只有一个1，所以10个维度的p（x）和q（x）计算交叉熵就只剩下一个维度了。公式很好推就不推了。

当某一次输入到网络中的是x，x表示某个数字，如果x与它对应的label y差的很远，那么loss很大，梯度回传进行参数更新。直到loss变的很小。

当sigmoid 遇到cross entropy

咦，两个交叉熵的公式不一样！！！

当然是不一样的，这里数据的label是下图这样的

举个栗子：

大家都知道sigmoid用于二分类问题，却不知道可以是多标签的二分类问题。

要对如下label的数据集进行分类

这个label是三个维度的，第一维表示性别：男女0/1,第二维代表头发：长发/短发， 第三维代表国籍：中国/其他。这个时候不是只有一个1，与one-hot不同，这是一个多标签的分类问题，每个维度之间是独立的。此时，sigmoid + cross entropy是分别对这三个维度计算概率, 这就是区别。他们之间的物理意义是不一样的。

 

总结一下：

sotfmax + cross entropy loss

适用场景：单标签多分类问题

label的所有维度加起来等于1，互相不独立，label是one-hot编码。

sigmoid + cross entropy loss

适用场景：多标签二分类问题

label的每一维都独立。

从概率分布上来讲，这两种组合其实就是对两种不同定义的概率分布进行学习的不同计算方法。

 

ps：以上只是博主的个人认知，如有错误，望指正。