【多任务学习】多任务学习中的自动任务选择和自动混合(AUTOSEM: Automatic Task Selection and Mixing in Multi-Task Learning)(二)
多任务学习(MTL)已经在许多问题领域上取得了成功,其目的是使用一些与主任务相关的辅助任务来提高主任务的性能。但是,当辅助任务的有用性比较低时,主要任务得不到有效的先验信息。MTL模型的成功取决于这些辅助任务的正确选择,以及在替代训练期间这些任务的平衡混合比。这两个问题可以通过对所有任务组合进行手动选择或超参数调整来解决,但是当候选辅助任务的数量非常大时,这会导致诱导偏差或不可实现。为了解决这些问题,提出了一个双步MTL流水线AUTOSEM方法,第一阶段通过贝塔伯努利多臂限制与Thompson Sampling自动选择最有用的辅助任务,第二阶段学习通过基于高斯过程的贝叶斯优化框架训练这些所选辅助任务的混合比。同时对GLUE语言理解任务进行了几次MTL实验,并表明AUTOSEM框架可以成功找到相关的辅助任务并自动学习它们的混合比例,从而在几个主要任务上实现显着的性能提升。
1、简介
多任务学习(MTL)(Caruana,1997)是一种归纳迁移机制,它利用相关任务的信息来改善主要模型的泛化性能。它通过在共享特征表示的同时并行训练多个任务来实现此目标,其中来自辅助任务的训练信号可以帮助改善主要任务的性能。尽管其性能令人印象深刻,但多任务学习系统的设计并非易事。想要使用来自其他辅助任务的知识来改善主要任务的绩效需要面临两个主要挑战:包括选择最相关的辅助任务以及学习平衡混合比,用于协同训练这些任务。人们可以通过所有任务组合进行手动选择或超参数调整来实现这一目标,但这会引入人为归纳偏差,或者当候选辅助任务的数量过大时难以实现。
在AUTOSEM框架中,第一阶段解决了从辅助任务池中选择自动任务的问题。为此,本文中使用非固定多臂赌博控制器(MAB),在训练循环内动态地交替选择任务,并最终返回每项任务对主要任务辅助效果的估计。我们将每个任务的效果建模为Beta分布,其预测值可以解释为每个任务对主要任务的训练性能做出非负贡献的概率。此外,我们将观察结果建模为伯努利变量,以便后验分布也是β分布的。我们使用Thompson抽样来进行权衡利用和探索。之后第二阶段使用在第一阶段选择出的辅助任务,并通过贝叶斯优化框架自动学习这些任务的训练混合比,通过将每个混合比率的性能建模为高斯过程(GP)从而搜索最佳值(Rasmussen,2004; Snoek等,2012)。对于GP中的协方差函数,我们使用Matern内核,该内核由平滑度超参数进行参数化,以便控制来自GP的样本的可微分性水平。此外,继霍夫曼等人之后(2011年),我们使用基于乐观和改进的决策组合作为提取函数(Shahriari等,2016),从GP搜索空间中选择下一个样本点。
2、模型
设s1和s2是我们分类任务中的输入句子对,我们通过双向LSTM-RNN对这些句子进行编码,类似于Conneau等人的工作(2017年)。接下来,我们对两个编码器的输出隐藏状态进行最大池化,其中u和v分别是s1和s2的max-pooing层的输出。稍后,我们将这两个表示(u和v)映射到单个富密集表示向量h中
h = [ u ; v ; u ∗ v ; ∣ u − v ∣ ] \mathrm{h}=[\mathrm{u} ; \mathrm{v} ; \mathrm{u} * \mathrm{v} ;|\mathrm{u}-\mathrm{v}|] h=[u;v;u∗v;∣u−v∣]
[;]表示相关性质, 表示u和v的元素乘法。我们将这个最终表示h投影到标签空间以对给定的句子对进行分类(参见图1)。我们还在我们的模型中使用ELMo(Peters等,2018)表示字嵌入。为此,我们为每个句子对提取三个ELMo层表示,并使用它们的加权和作为ELMo输出表示,其中权重是可训练的。
图2
3、多任务学习
在这项工作中,我们专注于改进任务(主要任务),允许它通过多任务学习(MTL)与相关辅助任务共享参数。设 { D 1 , … , D N } \left\{D_{1}, \ldots, D_{N}\right\} {D1,…,DN}为一组N个任务,我们将D1设置为主要任务,其余设置为辅助任务。我们可以通过增加具有N个投影层的模型,同时在这N个任务中共享其余模型参数,将我们的单任务学习基本模型(参见3.1节)扩展到多任务学习模型中(参见图1)。
我们基于混合比率 η 1 : η 2 : … : η N \eta_{1} : \eta_{2} : \ldots : \eta_{N} η1:η2:…:ηN在备用小批量中使用MTL训练这些任务,类似于先前的工作(Luong等人,2015),其中我们优化批次的任务i并转到下一个任务。
在MTL中,选择适当的辅助任务并适当调整混合比对于多任务模型的性能非常重要。尝试所有任务选择组合的天真方式难以处理。为了解决这个问题,我们在下一节中提出了AUTOSEM,这是一个两级流水线。在第一阶段,我们自动找到相关的辅助任务(在给定的N-1选项中),这些任务可以提高主要任务的性能。在找到相关的辅助任务后,在第二阶段,我们将这些选定的任务与主要任务一起进行,并自动学习他们的训练混合比例。
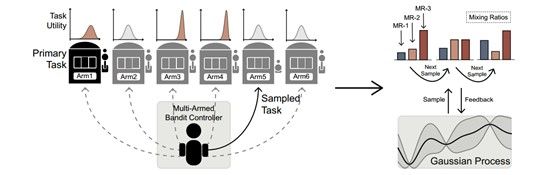
随着辅助任务的数量变得非常大,调整MTL中N个任务的混合比率会变得更加困难。但是,在大多数情况下,只有少数这些辅助任务可用于改进手头的主要任务。手动搜索相关任务的这种最佳选择是棘手的。因此,在这项工作中,我们提出了一种通过Thompson Sampling的多臂匪徒自动选择任务的方法(参见图2的左侧)。
设 [ a 1 , … , a N ] \left[a_{1}, \dots, a_{N}\right] [a1,…,aN]表示我们的多任务设置中赌博控制器的N个臂组(对应于任务组 { D 1 , … , D N } \left\{D_{1}, \ldots, D_{N}\right\} {D1,…,DN}),其中控制器选择序列在目前的培训轨迹上的行动/臂,以最大化预期的未来收益。在每轮 t b t_{b} tb,控制器基于噪声值估计选择臂并观察所选臂的奖励 r t b r_{t b} rtb。设 θ k \theta_{k} θk∈[0,1]为任务k的效用(有用性)。最初,选择器首先对 θ k \theta_{k} θk有独立的先验信念。我们将这些先验分布认为是带有两个参数 α k , β k \alpha_{k}, \beta_{k} αk,βk的β分布,先验分布概率方程为:
p ( θ k ) = Γ ( α k + β k ) Γ ( α k ) Γ ( β k ) θ k α k − 1 ( 1 − θ k ) β k − 1 \mathrm{p}\left(\theta_{k}\right)=\frac{\Gamma\left(\alpha_{k}+\beta_{k}\right)}{\Gamma\left(\alpha_{k}\right) \Gamma\left(\beta_{k}\right)} \theta_{k}^{\alpha k-1}\left(1-\theta_{k}\right)^{\beta_{k}-1} p(θk)=Γ(αk)Γ(βk)Γ(αk+βk)θkαk−1(1−θk)βk−1
其中Γ表示伽马函数。我们在第 t b t_{b} tb轮在伯恩利变量上得到奖励 r t b r_{t b} rtb∈{0,1},其中动作k产生为1的奖励(有概率为 θ k \theta_{k} θk,奖励为1,有概率为1- θ k \theta_{k} θk,奖励为0)。任务k的真实效用,即 θ k \theta_{k} θk,是未知的,并且可以或可以不随时间改变(基于任务效用的静止与非静止)。我们将奖励定义为对任务k进行抽样是否改进(或维持)主要任务的验证度量。
r t b = { 1 , if R t b ≥ R t b − 1 0 , otherwise r_{t b}=\left\{\begin{array}{c}{1, \text { if } R_{t_{b}} \geq R_{t_{b}-1}} \\ {0, \text { otherwise }}\end{array}\right. rtb={1, if Rtb≥Rtb−10, otherwise
其中 R t b R_{\mathrm{t}_{b}} Rtb表示在时间 t b t_{b} tb的主要任务的验证性能。通过上面的我们的上述设置,每个任务( θ k \theta_{k} θk)的作用可以直观地解释为具有任务k的多任务学习可以改善(或维持)主要任务的性能的概率。由于Beta分布的共轭性质我们更新数据也同样可以服从Beta分布,其参数可以使用简单的贝叶斯规则更新,其定义如下(Russo等,2018),
p ( θ ∣ r ) ∝ Bern θ ( r ) Beta α , β ( θ k ) p ( θ ∣ r ) ∝ Beta α + r , β + 1 − r ( θ k ) ( 4 ) ( α k , β k ) = { ( α k , β k ) if x t b s ≠ k ( α k , β k ) + ( r t b , 1 − r t b ) i f x t h s = k \begin{array}{l}{\mathrm{p}(\theta | \mathrm{r}) \propto \operatorname{Bern}_{\theta}(r) \operatorname{Beta}_{\alpha, \beta}\left(\theta_{k}\right)} \\ {\mathrm{p}(\theta | \mathrm{r}) \propto \operatorname{Beta}_{\alpha+r, \beta+1-r}\left(\theta_{k}\right) \quad(4)} \\ {\left(\alpha_{k}, \beta_{k}\right)=\left\{\begin{array}{c}{\left(\alpha_{k}, \beta_{k}\right) \quad \text { if } x_{t_{b}}^{s} \neq k} \\ {\left(\alpha_{k}, \beta_{k}\right)+\left(r_{t b}, 1-r_{t b}\right) \quad i f x_{t_{h}}^{s}=k}\end{array}\right.}\end{array} p(θ∣r)∝Bernθ(r)Betaα,β(θk)p(θ∣r)∝Betaα+r,β+1−r(θk)(4)(αk,βk)={(αk,βk) if xtbs̸=k(αk,βk)+(rtb,1−rtb)ifxths=k
其中 x t h s x_{t_{h}}^{s} xths是圆形 t b t_{b} tb处的采样任务。最后,在训练结束时,我们按如下方式计算每个臂的预期值:
E p = α k α k + β k \mathbb{E}_{p}=\frac{\alpha_{k}}{\alpha_{k}+\beta_{k}} Ep=αk+βkαk
这里,期望通过对该任务进行采样来测量改善(或维持)主要任务的概率。为了决定下一步采取的行动,我们应用Thompson Sampling(Russo等,2018;Chapelle和Li,2011)来进行权衡利用(最大化立即绩效)和探索(投资以积累新的信息,可能会改善未来的表现。在Thompson Sampling(Russo et al。,2018)中,我们不是采取最大化预期的动作k(即 arg max k E p [ θ k ] \arg \max _{k} \quad \mathbb{E}_{p}\left[\theta_{k}\right] argmaxkEp[θk]),而是从后验分布 θ k ∼ p ( θ k ) \theta_{k} \sim \mathrm{p}\left(\theta_{k}\right) θk∼p(θk)中随机抽取主要任务改进概率 θ k \theta_{k} θk。,并采取最大化采样主要任务来改进概率的动作k,即 larg max k θ k \operatorname{larg} \max _{k} \theta_{k} largmaxkθk。在训练结束时,任务选择可以通过期望阈值进行,也可以执行前K任务,并使用所选任务子集作为辅助任务运行第2阶段(详见第3.4节)

图2的右侧说明了我们的高斯过程控制器,用于自动学习MTL训练混合比(参见3.2节中的定义)。鉴于上一节中选择的辅助任务,下一步是找到一个适当的混合比率,训练这些选定的任务以及主要任务。通过对超参数值的大网格搜索手动调整此混合比率是非常消耗时间并且计算成本很高(即使所选辅助任务的数量很小)。因此,在我们的第二阶段,我们改为应用非参数贝叶斯方法来搜索近似最佳混合比。特别是,我们使用“高斯过程”通过自动折衷开采和勘探来顺序搜索混合比率。接下来,我们将详细描述高斯过程优化方法。
高斯过程(Rasmussen,2004;Snoek等,2012;Shahriari等,2016), G P ( μ 0 , k ) \mathrm{GP}\left(\mu_{0}, \mathrm{k}\right) GP(μ0,k),是一个非参数模型,完全由平均函数 μ 0 : χ ⟼ R \mu_{0} : \chi \longmapsto \mathbb{R} μ0:χ⟼R和正定核或协方差函数k: χ × χ ↦ R \chi \times \chi \mapsto \mathbb{R} χ×χ↦R.设 x 1 , x 2 , … , x n \mathbf{x}_{1}, \mathbf{x}_{2}, \dots, \mathbf{x}_{n} x1,x2,…,xn表示n个点的任何有限集合,其中每个 x i \mathbf{x}_{i} xi表示混合比的选择(即,第3.2节中描述的比率 η 1 , η 2 , … , η n \eta_{1}, \eta_{2}, \ldots, \eta_{n} η1,η2,…,ηn,并且 f i = f ( x i ) \mathrm{f}_{i}=\mathrm{f}\left(\mathrm{x}_{i}\right) fi=f(xi)是在 x i \mathbf{x}_{i} xi处评估的(未知)函数值(给定选择的混合比率的模型的真实性能)。设 y 1 , y 2 , … , y n \mathrm{y}_{1}, \mathrm{y}_{2}, \ldots, \mathrm{y}_{n} y1,y2,…,yn是相应的噪声观测值(训练结束时的验证性能)。在GP回归(GPR)的背景下, f = { f 1 , … , f n } \mathrm{f}=\left\{\mathrm{f}_{1}, \ldots, \mathrm{f}_{n}\right\} f={f1,…,fn}被认为是联合高斯(Rasmussen,2004), f ∣ X ∼ N ( m , K ) \mathrm{f} | \mathrm{X} \sim \mathrm{N}(\mathrm{m}, \mathrm{K}) f∣X∼N(m,K)其中, m i = μ 0 ( x i ) \mathrm{m}_{i}=\mu_{0}\left(\mathrm{x}_{i}\right) mi=μ0(xi)是平均向量, K i , j = k ( x i , x j ) \mathrm{K}_{i, j}=\mathrm{k}\left(\mathrm{x}_{i}, \mathrm{x}_{j}\right) Ki,j=k(xi,xj)是协方差矩阵。然后噪声观测 y = y 1 , y 2 , … , y n \mathrm{y}=\mathrm{y}_{1}, \mathrm{y}_{2}, \ldots, \mathrm{y}_{n} y=y1,y2,…,yn正常分布在f周围如下: f ∣ X ∼ N ( f , σ 2 I ) \mathrm{f} | \mathrm{X} \sim \mathrm{N}\left(\mathrm{f}, \sigma^{2} \mathrm{I}\right) f∣X∼N(f,σ2I)。
给定 D = ( x 1 , y 1 ) , … , ( x n 0 , y n 0 ) D=\left(x_{1}, y_{1}\right), \ldots,\left(x_{n 0}, y_{n 0}\right) D=(x1,y1),…,(xn0,yn0),随机初始观察的集合, X i \mathbf{X}_{i} Xi表示混合比率, Y i \mathbf{Y}_{i} Yi表示相应模型的验证性能。接下来,我们基于如上所述的这些初始观察对GP进行建模。我们从该GP中采样下一个点 x n 0 + 1 x_{n 0+1} xn0+1(在我们的例子中为混合比)并获得其相应的模型性能$$,并且现在考虑到n0+1点再次更新GP(Rasmussen,2004)。我们继续这个过程以进行固定的步骤。接下来,我们将讨论我们如何执行采样(基于采集函数)和用于cal-2Note的内核。
采集方程 在这里,我们描述了用于决定下一个采样位置的采集方程。虽然人们可以选择最大化平均功能的点,但这并不总能带来最好的结果(Hoffman等,2011)。由于我们还有估计的方差以及每个点的平均值,我们可以将此信息合并到优化中。在这项工作中,我们使用GP-Hedge方法(Hoffman等,2011;Auer等,1995),其概率性地选择三个获取函数之一:改进概率函数,预期改进函数和上限置信度函数。改进采集功能的概率测量采样混合比率到目前为止 ( τ ) P ( f ( x i ) > τ ) (\tau) \quad P\left(f\left(x_{i}\right)>\tau\right) (τ)P(f(xi)>τ)的最佳观测值的改进的概率。预期的改进还包括改进量 E [ ( f ( x i ) − τ ) I ( f ( x i ) > τ ) ] \mathrm{E}[(\mathrm{f}(\mathrm{xi})-\tau) \mathrm{I}(\mathrm{f}(\mathrm{xi})>\tau)] E[(f(xi)−τ)I(f(xi)>τ)]。对于某些超参数λ,高斯过程上置信界(GP-UCB)算法测量采样混合比的乐观性能上限(Srinivas等,2009), μ i ( x i ) + λ σ i ( x i ) \mu_{i\left(x_{i}\right)}+\lambda \sigma_{i}\left(x_{i}\right) μi(xi)+λσi(xi)。
马特恩核 协方差函数(或kerel)定义了高斯过程中两点的接近度或相似度。在这里,我们使用自动相关性确定(ARD)Matern kernel(Rasmussen,2004),其通过ν>0参数化来控制平滑度。特别是来自具有这种核的GP的样本是可微分的。当ν是半整数时(即对于非负整数p,ν=p+1/2),协方差函数是指数p和p阶多项式的乘积。在机器学习的背景下,ν的通常选择包括3/2和5/2(Shahriari等,2016)
4、训练细节
我们使用预先训练的ELMo来获取句子表示作为我们模型的输入(Peters等,2018),实现基于Scikit-Optimize的高斯过程,我们大多数配置使用默认配置。我们使用准确性作为所有任务的验证标准。对于除QNLI和SST-2之外的所有实验,我们将早期停止应用于验证性能平台。当主要任务是分类时,候选任务组包括所有2句分类任务。当主要任务是单个句子的分类时,它由两个句子组成,而它包括所有两句话和单句子分类任务。由于多臂赌博控制器的效用估计是含有噪声的的,我们选择前两个基于预期任务效用估计的任务,如果其效用估计值高于0.5,则包括其他任务。除非明确提到,否则报告的所有结果都是具有两次运行(具有不同随机种子)的相同实验的集合。我们使用隐藏单元大小为1024的两层LSTM-RNN用于RTE,512个单元用于其余模型,并且使用AdamOptiizer(Kingma和Ba,2014)。阶段1中每个任务的先前参数设置为 =1, =1,这些参数通常用于其他阶段。对于阶段1,赌博控制器在训练期间迭代地选择来自不同任务的批量数据,以了解每个辅助任务的近似重要性(Graves等,2017)。在阶段2(高斯过程)中,我们依次绘制混合比例样本并在完全训练后评估每个样本(Snoek等,2012)。在没有太多调整的情况下,我们使用了大约200轮用于基于阶段1赌博的方法,其中每轮由大约10个小批量的优化组成。对于第二阶段,我们用15和20作为绘制样本的数量进行了实验,发现MRPC的15个样本和其余任务的20个样本运行良好。这使得我们的两级流水线的总计算成本大约为(15+1)x和(20+1)x,其中x表示为给定任务运行基本模型模型所花费的时间。这比基于网格搜索的手动调整混合比设置(它可以根据任务数量指数扩展)显着更有效。