大数据与算法系列之排序算法

排序算法是从事IT行业中最为常见的算法，排序是数值计算基础，本次将讲解各种排序算法。

一般情况下的算法思想是通过两两比较的方式进行排序，虽然从理论上来讲采用两两比较可以解决现实问题，但是实际上却不会采用两两比较的方式，因此，本次将会介绍性能较高的爱须算法，也是实际中用的最多的方法。

快速排序

快速排序(Quick Sort)采用分治法的思想，首先把一个数值序列划分为两个子序列，然后对两个子序列再进行分治法的思想，计算过程如下：

1. 从数值队列中选择一个基准元素
2. 将队列中的其他元素与基准元素进行比较，比基准元素小的元素放在基准元素的左边，比基准元素大的元素放在右边(降序排列则相反)，则队列被基准元素划分为左右两个区间。
3. 对两个区间的值分别递归步骤2，使其最终形成有序的序列。

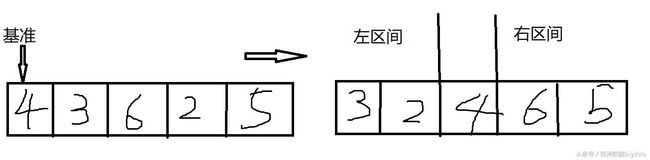
虽然上述步骤是采用递归的方式，但是当区间小于等于1时，将会直接返回，因此不会无限制的递归下去，例如，对于队列数值‘4、3、6、2、5’采用快速排序进行升序排列过程如图所示：

快速排序基准区间划分

以‘4’为基准，将比其小的元素‘3’，‘2’放到‘4’的左边，比其大的‘6’，‘5’放到右边，形成以4为基准的左右区间，然后对左右区间分别再次选择出基准元素，重复上述过程，最终得到序列值‘2’，‘3’，‘4’，‘5’，‘6’

快速排序的时间复杂度O(nlogn)，空间复杂度与具体的实现有关。

归并排序

归并排序(Merge Sort)是指将两个已经有序的序列合并成一个有序序列的排序方式。归并排序可以采用迭代的方式进行排序。例如，有两组数值序列A、B，采用归并排序进行升序排序，则排序步骤如下

1. 申请存放最终合并后的数值序列存放空间，空间大小为数值序列A、B的空间纸盒
2. 初始化两个指针，分别指向数值序列A、B的收元素地址
3. 比较两个指针对应的值，将较小的值放入到最终存放空间，并移动较小指针到序列的下一位置
4. 重复步骤3，直到某个指针已经到序列的队尾，且没有元素可以和另外一个序列进行比较
5. 将另外一个序列的剩余元素直接复制到最终 序列存放空间的末尾

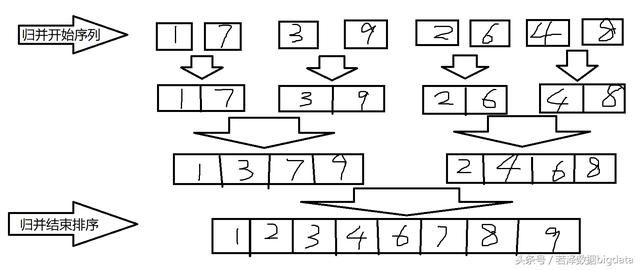
例如，两组数值序列A、B，可以采用递归的思想，将一个大的序列拆分成两组子序列，然后对两组子序列再次进行拆分，直到每个子序列中仅有一个元素，然后将两个只有一个元素的序列归并为一个含有两个元素的序列，再将两个含有两个元素的序列进行归并，以此类推，直到所有的元素都完成归并，如图：

归并排序方法的时间复杂度：最差时间复杂度O(nlogn)(不理解复杂度的，请看本人上一篇文章)，最优时间复杂度O(n)，平均复杂度O(nlogn)

归并排序方法的空间复杂度：具体与实现方法有关，不应高于O(n)

推排序

对排序(Heap Sort)是基于推的数据结构实现的排序算法，推是一种日常中使用较多的数据结构，对于含有N个数值序列的{X1,X2,X3.....Xn}，若满足Xi小于等于K2i且Ki小于等于K2i+1其中(1<=i<=n/2)则可以称作小根推，小根堆是堆顶的元素值，且是堆所有元素节点最小的值，相反，当Xi大于等于K2i且Ki大于等于K2i+1，即堆顶的元素值是堆里所有节点关键字中最大的值，称作大根堆。

根据上面描述，最小堆的第0个元素是整个堆中的最小值，最大堆的第0个元素是整个堆中的最大值

由于堆顶元素是最大值或最小值，所以可以利用此特性，每次从数组中直接选取出最大值或者最小值，使每次排序变的相对简单，推排序的实现步骤氛围以下4步：

1. 将初始元素值X1,X2,X3......Xn构建大根推(最大堆)
2. 将堆顶元素Xi与最后一个元素Xn置换，此时可将所有排序元素区分为两个部分，其中，置换后的Xn属于有序集合，前序元素{X1,X2,X3......Xn}属于无序集合
3. 根据步骤2的结果，将无序集合中的元素再洗进行大根堆调整，将得到的堆顶元素与最后的Xn-1置换，德大有序集合{Xn,Xn-1}及无需集合X1,X2,X3......Xn-2}
4. 重复上述过程直到无序集合中的数据小于2，然后将有序几个与无序集合的最后一个元素合并，最终得到完成的有序集合

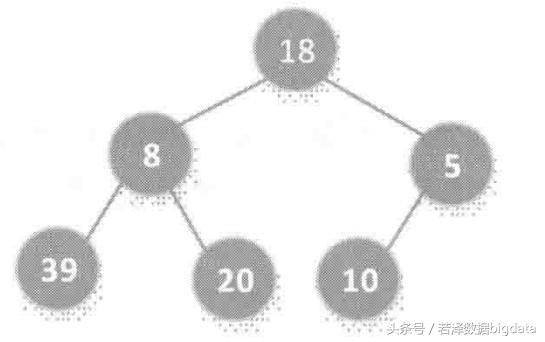
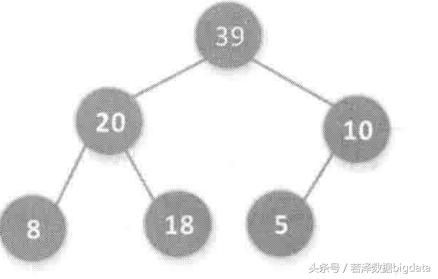
排序元素的升序排序或者降序排序，取决于排序过程采用的是最小堆结构还是最大堆结构，以给定数组A[6]={18,8,5,39,20,10}为例，进行构建堆

首先构造一个二叉树

构建初始堆

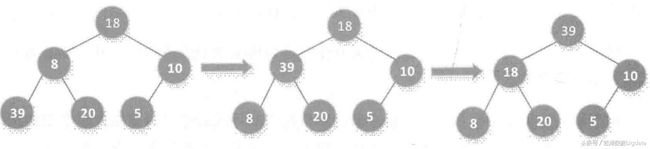
元素18所在的子树找那个不满足堆的性质，因此进一步调整后，从完全二叉树最后一个非叶子节点开始，使子节点与当前节点进行比较，将最大的值做哦为当前节点，一次调节左子树和右子树

重复迭代进行堆排序，最终获得从大到小的排序结果

此外还有基数排序，外排序等，不做具体介绍了。喜欢的话，点一下关注吧！每天都有文章哦！