数据结构————查找与排序
复习了几遍数据结构,线性表、栈、队列、串、数组、广义表、树、图、查找和排序。发现查找和排序算法很容易忘,而且这些算法又是很经典的,其他的掌握结构体和指针稍微好一点,想在此写下查找和排序算法,让自己更深刻,很多都不好写,所以有些就没写。
查找
1.基于线性表查找法 静态查找表 不对表做插入和删除
顺序查找法 : 就是遍历一遍进行if判断 平均查找长度 (n+1)/2;
int SeqSearch(RecordList l,KeyType k)
{
l.r[0].key=k;i=l.length;
while(l.r[i].key!=k)
i--;
return i;
}
折半查找法 : 顺序存储,有序排序,优点:比较次数少,查找速度快,平均性能好;缺点:待查表为有序表,且插入删除困难,适合用于不经常变动而查找频繁的有序列表。 平均查找长度 log2(n+1)-1
int BinSrch(RecordList l,KeyType k)
{
low=1;high=l.length;
while(low<=high)
{
mid=(low+high)/2;
if(k==l.r[mid].key) return mid;
else if(k
分块查找法 :性能介于顺序查找和折半查找之间
25 ->{18,14,12,25 } 58->{8,28,32,45,36,58} 88->{60,88,71}
| 25 | 58 | 88 |
| 18 | 14 | 12 | 25 | 8 | 28 | 32 | 45 | 36 | 58 | 60 | 88 | 71 |
2.基于树的查找法 动态查找表:需要对表做插入和删除
二叉排序树 :平均查找长度 log2(n) 与折半查找相差不大,插入和删除结点十分方便,对于经常做插入、删除、查找运算的表,采用二叉排序树结构。
BSTree SearchBST(BSTree bst,KeyType key)
{
if(!bst) return NULL;
else if(bst->key==key) return bst;
else if(bst->key>key) return SearchBST(bst->lchild,key);
else
return SearchBST(bst->rchild,key);
}平衡二叉树 : 又称AVL树,左子树与右子数的高度之差的绝对值小于等于1,引入平衡二叉排序树目的:为了提高查找效率,平均查找长度为 log2(n)
B树: 与二叉树类似,可以定义一种“m叉排序树”,通常称为m路查找树
如果m路查找树为平衡树时,其查找性能更好 B树即为一颗平衡的m路查找树,或者空树
1.树中每个结点最多有m棵子树 2.根结点至少有两棵子树
3.除根结点之外的所有非叶结点至少有m/2棵子树
例:具有n个叶结点的m阶B树,至少含有多少个关键字? 答:1+(【m/2】-1)*(n-1)
3.计算式查找法—哈希法
哈希法又称散列法、杂凑法或关键字地址计算法
构造哈希函数 1.数字分析法 2.平方取中法 3.分段叠加法 4.除留余数法 5.伪随机数法
处理冲突的方法: 1.开放定址法 2.再哈希法 3.链地址法 4.建立公共溢出区
1.开放定址法 (1)线性探测再散列 d=1,2,3,4,5,6················
(2)二次探测再散列 d=1*1 ,-1*1,2*2,-2*2,·············k*k,-k*k
(3) 伪随机数序列 建立一个随机数发生器
3.链地址法 经常进行插入和删除
排序
1.插入类排序
直接插入排序: 时间复杂度 T=O(n^2); 空间复杂度 S=O(1) 稳定
void InsSort(RecordType r[],int length)
{
for(i=2;i<=length;i++)
{
r[0]=r[i];j=i-1;
while(r[0].key{48} 62 35 77 55 14 35 98
{48 62} 35 77 55 14 35 98
{35 48 62} 77 55 14 35 98
{35 48 62 77} 55 14 35 98
{35 48 55 62 77} 14 35 98
{14 35 48 55 62 77} 35 98
{14 35 35 48 55 62 77} 98
{14 35 35 48 55 62 77 98}
折半插入排序: 时间复杂度O(n^2) 比较时间复杂度 nlogn 空间复杂度 O(1) 不稳定
void BinSort(RecordType r[],int length)
{
for(i=2;i<=length;i++)
{
x=r[i];
low=1;high=i-1;
while(low<=high)
{ mid=(low+high)/2;
if(x.key=low;--j) r[j+1]=r[j];
r[low]=x;
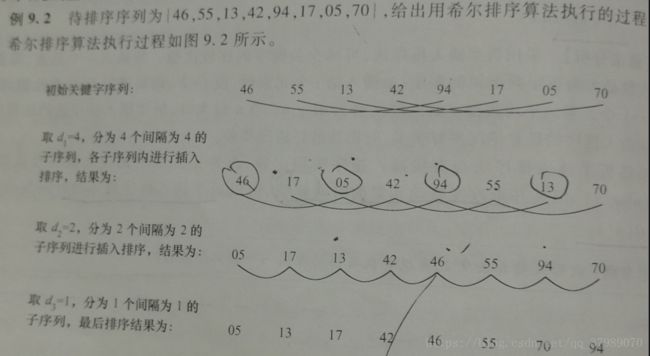
}} 希尔排序: 时间复杂度O(n^1.5) 空间复杂度O(1)
void ShellInsert(RecordType r[],int length,int delta)
{
for(i=1+delta;i<=length;i++)
if(r[i].key0&&r[0].key 2.交换类排序
冒泡排序: 时间复杂度O(n^2) 空间复杂度O(1) 稳定
void BubbleSort(RecordType r[],int n)
{
change=TRUE;
for(i=1;ir[j+1].key)
{ x=r[j]; r[j]=r[j+1]; r[j+1]=x;
change=TRUE;
}
}
} 序列 {48,62,35,77,55,14,35,98,22,40}进行冒泡排序
第一趟 48 35 62 55 14 35 77 22 40 98
第二趟 35 48 55 14 35 62 22 40 77 98
第三趟 35 48 14 35 55 22 40 62 77 98
第四趟 35 14 35 48 22 40 55 62 77 98
第五趟 14 35 35 22 40 48 55 62 77 98
第六趟 14 35 22 35 40 48 55 62 77 98
第七趟 14 22 35 35 40 48 55 62 77 98
快速排序: 时间复杂度 nlog2(n) 空间复杂度 log2(n) 不稳定
void QKSort(RecordType r[],int low,int high)
{
if(low=x.key)
high--;
if(low 3.选择类排序
简单选择排序: 时间复杂度O(n^2) 空间复杂度O(1) 不稳定
void SelectSort(RecordType r[],int n)
{
for(i=1;i<=n-1;++i)
{
k=i;
for(j=i+1;j<=n;++j)
if(r[j].key{48 62 35 77 55 14 35 98 }
14 {62 35 77 55 48 35 98 }
14 35 {62 77 55 48 35 98 }
14 35 35 {77 55 48 62 98}
14 35 35 48 {55 77 62 98}
14 35 35 48 55 62 77 98
树形选择排序: 时间复杂度:O(nlog2(n)) 空间复杂度O(n) 稳定
堆排序: 时间复杂度 O(nlog2(n)) 空间复杂度O(1) 不稳定
void sift(RecordType r[],int k,int m)
{ /*以r[k]为根的完全二叉树,分别以r[2k]和r[2k+1]为根的左右子树*/
t=r[k]; x=r[k].key; i=k; j=2*j;
finished=FALSE;
while(j<=m&&!finished)
{
if(j+1<=m&&r[j].key=r[j].key) finished=TRUE;
else
{r[i]=r[j];i=j;j=2*i;}
}
r[i]=t;
}
void crt_heap(RecordType r[],int n)
{
for(i=n/2;i>=1;--i)
sift(r,i,n);
}
void HeapSort(RecordType r[], int n)
{
crt_heap(r,n);
for(i=n;i>=2;--i)
{
b=r[1]; r[1]=r[i]; r[i]=b;
sift(r,1,i-1);
}
}
4.归并排序
归并排序:将两个或者以上的有序表合并成一个新的有序表 时间复杂度O(nlog2(n)) 空间复杂度O(n) 稳定
5.分配类排序
多关键字排序
链式基数排序: O(d(n+rd)) O(rd) 稳定