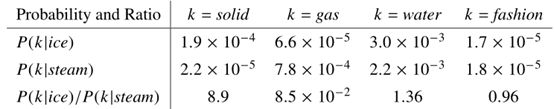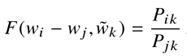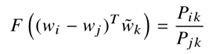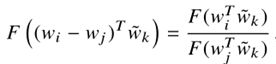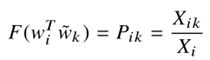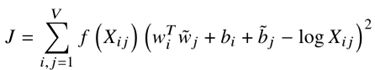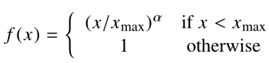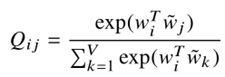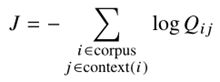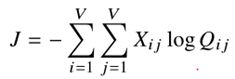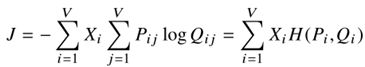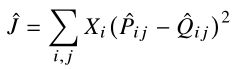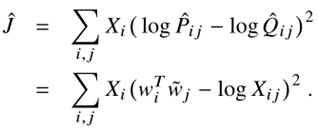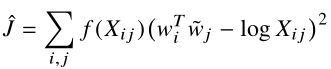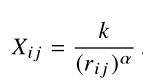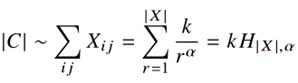GloVe模型介绍
GloVe
本模型结合了以下两个主要模型族的优点:全局矩阵分解和局部上下文窗口方法。我们的模型只训练单词-单词共现矩阵中的非零元素,而不是整个稀疏矩阵或单个上下文窗口的大型语料库,从而有效地利用统计信息。该模型生成了一个具有意义子结构的向量空间,其在最近的一次单词类比任务中的性能为75%。在相似性任务和命名实体识别方面,它也优于相关模型。
1 介绍
大多数的词向量方法都依赖于词向量对之间的距离或角度作为评价这类词表示的本质质量的主要方法。目前有一种新的基于词的类比的方法,通过考察词向量之间的标量距离,而不是词向量之间的各种维数的差异,来研究词向量空间的精细结构。例如:“king is to queen as man is to woman”可表示为king −queen = man – woman
如潜在语义分析(LSA)和本地上下文窗口的方法,如skip-gram模型。目前,这两个方法都存在明显的缺陷。虽然像LSA这样的方法有效地利用了统计信息,但它们在单词类比任务上的表现相对较差,表明向量空间结构不够理想。像skip-gram这样的方法可能在类比任务上做得更好,但是它们不能很好地利用语料库的统计数据,因为它们是在单独的本地上下文窗口上训练的,而不是在全局共现计数上。
在这项工作中,我们分析了产生线性意义方向所必需的模型性质,并认为全局对数-双线性回归模型适合于这样做。提出了一种特殊的加权最小二乘模型,用于训练全局词与词的共现计数,从而有效地利用统计量。
2 相关工作
2.1 矩阵分解方法
用于生成低维单词表示的矩阵分解方法可以追溯到LSA。这些方法利用低秩近似来分解大型矩阵,从而获取语料库的统计信息。这些矩阵捕获的特定信息类型因应用程序的不同而不同。在LSA中,矩阵属于“term-document”类型,即,行对应单词或术语,列对应语料库中的不同文档。相反,超空间类比语言(HAL)利用“term-term”类型的矩阵,即,行和列对应单词,条目对应给定单词在另一个给定单词上下文中出现的次数。
HAL和相关方法的主要问题是最常见的单词贡献不成比例的相似性测量:两个词与and或者the共现的次数,将会对它们的相似性产生很大的影响,尽管表达的语义相关度相对较少。有许多技术可以解决HAL的这一缺点,比如COALS ,其中共现矩阵首先通过基于熵或相关关系的归一化进行转换。这种类型转换的一个优点是对原始的共现计数进行压缩,以便在更小的间隔内更均匀地分布。对于大小合理的语料库,共现计数可能跨越8或9个数量级。
2.2 基于窗口的方法
另一种方法是学习有助于在本地上下文窗口中进行预测的单词表示。与矩阵因子分解方法不同,基于窗口的方法的缺点是不能直接对语料库的共现统计量进行操作。相反,这些模型在整个语料库中扫描上下文窗口,这无法利用数据中大量的重复。
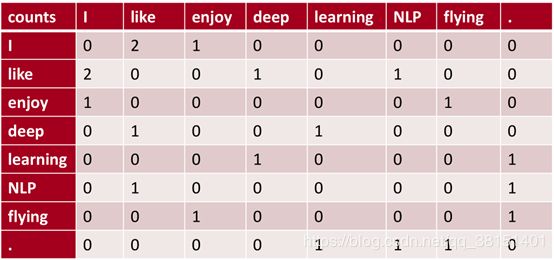
| 举例:假设有如下语料库,构建基于窗口的共现矩阵
|
3 GloVe 模型
词出现在语料库的统计数据是信息的主要来源,所有非监督方法学习单词的问题在于如何从这些统计数据生成意义,以及由此产生的词向量可能代表的意义。于是构造了一种新的单词表示模型,我们称之为GloVe ,用于全局向量,因为全局语料库统计数据是由该模型直接捕获的。
一些概念及符号:
X:词与词的共现计数用表示
![]() :将单词j在单词i上下文中出现的次数列成表
:将单词j在单词i上下文中出现的次数列成表
![]()
![]() :是任何单词在单词i上下文中出现的次数
:是任何单词在单词i上下文中出现的次数
![]()
![]() :为单词j出现在单词i上下文中的概率
:为单词j出现在单词i上下文中的概率
| 我们从一个简单的例子开始,它展示了如何从共现概率中直接提取意义的某些方面。例如,考虑两个单词i和j,我们可以取i =冰,j =蒸汽。这些词之间的关系可以通过研究它们与各种探测词k的共出现概率的比值来检验。对于与冰有关而与蒸汽无关的词k,比如k = solid,我们预计 |
上述论证表明,单词矢量学习的合适起点应该是共现概率的比值,而不是概率本身。注意到![]() 的比值取决于i、j和k三个单词,最一般的模型采用这种形式:
的比值取决于i、j和k三个单词,最一般的模型采用这种形式:
其中:
![]() :是单词向量
:是单词向量
![]() :是独立的上下文单词向量
:是独立的上下文单词向量
F可能依赖于一些尚未指定的参数。
F的可能性是巨大的,但是通过强制执行一些操作,我们可以得到一个唯一的选择。
- 首先,我们希望F编码的信息在向量空间中以
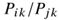 的比例表示。由于向量空间本质上是线性结构,因此最自然的方法是使用向量差。在此基础上,我们可以将考虑范围限制在仅依赖于两个目标词的差值的函数F上,即修改上述等式为:
的比例表示。由于向量空间本质上是线性结构,因此最自然的方法是使用向量差。在此基础上,我们可以将考虑范围限制在仅依赖于两个目标词的差值的函数F上,即修改上述等式为:
- 接下来,我们注意到上式中的F的自变量是向量,而右边是标量。虽然F可以被看作是一个复杂的函数参数化,例如,一个神经网络,这样做会混淆我们试图捕捉的线性结构。为了避免这个问题,我们可以先取参数的点积,这可以防止F以不合适的方式混合向量维数:
- 接下来,注意对于单词-单词共现矩阵,单词和上下文单词之间的区别是任意的,我们可以自由地交换这些单词。这样做,我们不仅必须交换
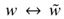 还有
还有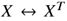 。在这种重新标记下,最终的模型应该是不变的,但是Eqn(3)不是。然而,对称可以通过两个步骤恢复。首先,我们要求F是组
。在这种重新标记下,最终的模型应该是不变的,但是Eqn(3)不是。然而,对称可以通过两个步骤恢复。首先,我们要求F是组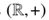 和
和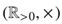 之间的同态,即:
之间的同态,即:
- 由Eqn(3)求出:
- Eqn(4)的解是F 为:
- 接下来,我们注意到,如果不是右边的
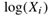 , Eqn(6)将显示交换对称性。然而,这一项与k无关,所以它可以被吸收到偏置
, Eqn(6)将显示交换对称性。然而,这一项与k无关,所以它可以被吸收到偏置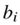 中,为了
中,为了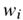 。最后,为
。最后,为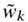 添加一个额外的偏置
添加一个额外的偏置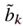 恢复对称性:
恢复对称性:
Eqn(7)是对Eqn(1)的一个极大的简化,但实际上它的定义是错误的,因为对数在参数为0时发散。解决这个问题的一个方法是在对数![]() 中添加一个移位,它在保持X的稀疏性的同时避免了分歧。该模型的一个主要缺点是,它对所有同时发生的事件都具有同等的权重,即使是那些很少发生或从未发生的事件。
中添加一个移位,它在保持X的稀疏性的同时避免了分歧。该模型的一个主要缺点是,它对所有同时发生的事件都具有同等的权重,即使是那些很少发生或从未发生的事件。
- 针对这些问题,提出了一种新的加权最小二乘回归模型。将Eqn(7)转化为最小二乘问题,在代价函数中引入加权函数
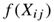 ,得到了该模型:
,得到了该模型:
其中:
V:词汇表的大小
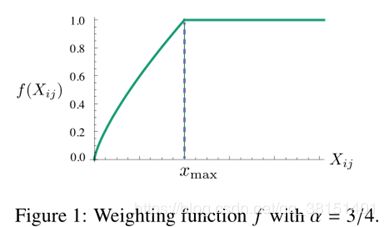
函数f应遵循如下规则:
- f(0) = 0。如果f是连续的函数,它应该在x→0时快速消失,足够使
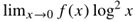 是有限的。
是有限的。 - f (x)应该是不递减的,这样就不会出现罕见的共现。
- 对于较大的x值,f (x)应该相对较小,这样就不会对频繁出现的共存项进行加权。
当然,很多函数都满足这些性质,但是我们发现有一类函数可以很好地参数化:
3.1 与其他模型的关系
skip-gram或ivLBL方法的起点是一个模型![]() ,表示单词j出现在单词i上下文中的概率。
,表示单词j出现在单词i上下文中的概率。
- 假设
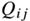 是一个softmax函数:
是一个softmax函数:
- 全局目标函数可以写成:
- 然而,Eqn(11)中的和可以更有效地计算,如果我们首先把i和j值相同的项放在一起:
其中X表示共现矩阵。
- 由于
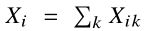 ,
,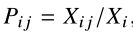 ,我们可以将Eqn(12)重写为:
,我们可以将Eqn(12)重写为:
其中:![]() 是pi和qi分布的交叉熵,我们用xi来类比。该目标作为交叉熵误差的加权和,与Eqn(8)的加权最小二乘目标具有一定的形式化相似性。
是pi和qi分布的交叉熵,我们用xi来类比。该目标作为交叉熵误差的加权和,与Eqn(8)的加权最小二乘目标具有一定的形式化相似性。
首先,交叉熵误差只是概率分布之间许多可能的距离度量之一,它对不太可能发生的事件给予了过多的权重。此外,要使测度有界,需要对模型分布Q进行适当的归一化。这提出了一个计算瓶颈,由于整个词汇在Eqn(10)求和,它将需要考虑不同的距离测量。一个自然的选择是一个最小二乘目标,其中Q和P中的归一化因子被丢弃:
其中,![]() ,
,![]()
- 由于
 通常是非常大的值,又带来了新的问题,使得优化变得复杂,一个方式是使用对数的平方误差来代替:
通常是非常大的值,又带来了新的问题,使得优化变得复杂,一个方式是使用对数的平方误差来代替:
- 最后,我们观察到,虽然权重因子xi是由skip-gram和ivLBL模型固有的在线训练方法预先设定的,但它并不能保证是最优的。事实上,Mikolov等人观察到,可以通过过滤数据来提高性能,从而降低频繁单词权重因子的有效值。考虑到这一点,我们引入了一个更一般的加权函数,我们也可以自由地使用它来依赖上下文单词。其结果是:
它等价于我们之前推导出的Eqn(8)的代价函数。
3.2 模型的复杂性
根据Eqn(8)可知,模型的复杂性取决于共现矩阵X中非零元素的数目。然而,典型的词汇有成千上万的单词,因此可以对X的非零元素的数量进行更严格的限制。为了对X中非零元素的数量作出任何具体的说明,有必要对单词共现的分布做一些假设。
- 特别地,我们假设单词i与单词j共出现的次数
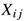 可以建模为该词对频率秩的幂函数:
可以建模为该词对频率秩的幂函数:
- 语料库中的单词总数与共现矩阵X中所有元素的和成正比:
以下推导有些复杂,不再赘述
4 实验
4.1 评价方法
- 词的类比:“a is to b as c is to ?”
语义问题:典型的人或地方的类比,like “Athens is to Greece as Berlin is to ?”
语法问题:动词时态或形容词的形式,like “dance is to dancing as fly is to ?”
我们根据余弦相似度,通过找到表示![]() 最接近
最接近![]() 的单词d来回答“a is to b as c is to ?”的问题。
的单词d来回答“a is to b as c is to ?”的问题。
- 词汇相似度
- 命名实体识别:
四种实体类型:人员、位置、组织和杂项
- 语料库和训练细节
我们标记和小写与斯坦福记号赋予器每个语料库,构建一个最频繁的词汇的400000字,然后构造一个矩阵的共存计数X。在构造X时,我们需要考虑要选择多大的上下文窗口以及是否要区分窗口左边和右边的单词。我们将在下面探讨这些选择的效果。在所有的情况下,我们都使用一个递减加权函数,这样的话,单词对中间隔为d个单词的单词对占总数的1/d。这是一种解释这一事实的方法,即非常遥远的词对应该包含关于单词之间关系的相关信息较少。
对于我们所有的实验,我们设置![]() ,α= 3/4,和训练模型使用AdaGrad ,随机抽样的非零元素x,最初的学习速率为0.05。我们对小于300维的向量执行50次迭代,否则执行100次迭代。除非另有说明,我们使用的上下文是左边十个单词和右边十个单词。
,α= 3/4,和训练模型使用AdaGrad ,随机抽样的非零元素x,最初的学习速率为0.05。我们对小于300维的向量执行50次迭代,否则执行100次迭代。除非另有说明,我们使用的上下文是左边十个单词和右边十个单词。
该模型生成了两组词向量,W和![]() ,当X对称时,W和
,当X对称时,W和![]() 是等价的,只是由于它们的随机初始化而不同;这两组向量应该相等。另一方面,有证据表明,对于某些类型的神经网络,对网络的多个实例进行训练,然后将结果结合起来,可以帮助减少过拟合和噪声,总体上提高结果。考虑到这一点,我们选择用W +
是等价的,只是由于它们的随机初始化而不同;这两组向量应该相等。另一方面,有证据表明,对于某些类型的神经网络,对网络的多个实例进行训练,然后将结果结合起来,可以帮助减少过拟合和噪声,总体上提高结果。考虑到这一点,我们选择用W + ![]() 的和作为单词向量。这样做通常会在性能上有一个小的提升,其中语义类比任务的提升最大。
的和作为单词向量。这样做通常会在性能上有一个小的提升,其中语义类比任务的提升最大。
4.2 模型分析
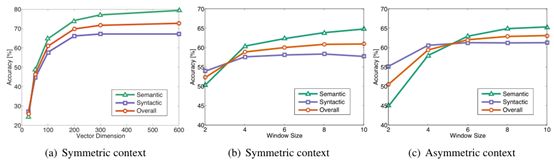
- 向量长度和上下文大小
- 观察到大于200维的向量的准确率提升效果变差
- 我们研究了改变对称和非对称上下文窗口的窗口大小的影响。对于小而不对称的上下文窗口,语法子任务的性能更好,这与直觉一致,即语法信息主要来自即时上下文,并且可以强烈依赖于词序。另一方面,语义信息通常是非本地的,并且更多的信息是用更大的窗口大小捕获的。
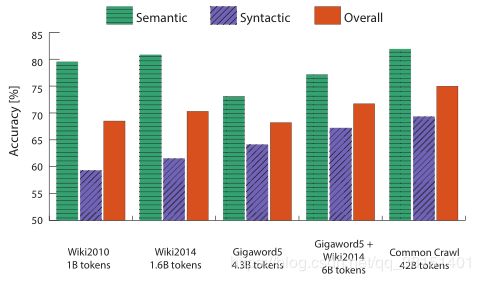
- 语料库的大小
在句法子任务上,随着语料库规模的增大,其性能呈单调增长。这是意料之中的,因为较大的语料库通常会产生更好的统计数据。有趣的是,同样的趋势在语义子任务上并不成立,在较小的Wikipedia语料库上训练的模型比在较大的Gigaword语料库上训练的模型做得更好。这可能是由于类比数据集中有大量基于城市和国家的类比,而且维基百科对大多数这样的地点都有相当全面的文章。此外,维基百科的条目是为了吸收新知识而更新的,而Gigaword是一个固定的新闻存储库,其中包含过时的、可能不正确的信息。
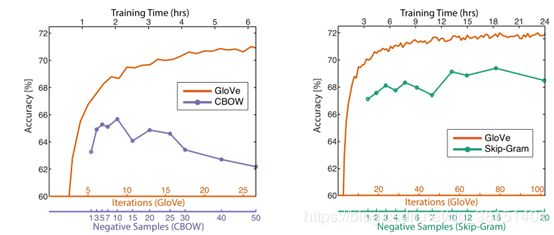
- 运行时间
- 与word2vec对比
总运行时间被划分为填充(构造)X所需时间和训练模型所需时间。前者取决于许多因素,包括窗口大小、词汇量大小和语料库大小。
我们注意到,如果负样本数超过10,word2vec的性能实际上会下降。这可能是因为负抽样法不能很好地逼近目标概率分布。
在相同的语料库、词汇量、窗口大小和训练时间下,GloVe始终优于word2vec。
5 结论
最近,相当多的注意力集中在分布式单词表示是否是最好的学习方法,是基于计数的方法还是基于预测的方法。基于预测的模型获得了大量支持,基于计数的方法捕获全局统计的效率可能是有利的。但是。我们构建了一个模型,该模型利用计数数据的这一主要优点,同时捕获最近流行的基于对数双线性预测的方法(如word2vec)中有意义的线性子结构。结果,Glove是一个新的全局对数双线性回归模型,用于无监督学习的单词表示,它优于其他模型在单词类比,单词相似性,和命名实体识别任务。
------------------------------------------------------------------------------------------------
参考资料:https://nlp.stanford.edu/pubs/glove.pdf