选择排序,冒泡排序,归并排序,快速排序,直插排序算法实现以及算法分析
一.排序算法原理及实现
1. 选择排序(select_sort)
(1)原理:
第一步:在1~n个数中找出最小数,然后与第1个数交换,前1个数排好;
第二步:在2~n个数中找出最小数,然后与第2个数交换,前2个数排好;
……
第n-1步:在n-1~n个数中找出最小数,然后与第n-1个数交换,排序结束。
(3)算法复杂度分析:
选择排序的比较次数与关键字的初始状态无关,总的比较次数N=(n1)+(n-2)+……+1=n*(n-1)/2,所以比较次数O(n2)。其交换次数最好情况是已经有序,交换0次;最坏情况是逆序,交换n-1次。交换次数是O(n),而复制操作在0到3(n-1)之间。所以选择排序平均算法复杂度为O(n^2)。
(4)测试结果(数据规模从10000到60000):
![]()
结果分析:由于直接选择排序算法的时间复杂度为O(n^2),随着数据规模的增加,算法的执行时间增长地越快。
2. 冒泡排序(bubble_sort)
(1) 原理:
- 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。

(3)算法复杂度分析:
其比较次数是 n*(n-1)/2,交换次数介于0到n*(n-1)/2之间,所以平均其复杂度是O(n^2)。
(4)测试结果(数据规模从10000到60000):
![]()
结果分析:冒泡排序算法的时间复杂度为O(n^2),跟直接选择排序一样,但是其比直接选择排序算法数组元素交换的次数要更多,由于交换所需CPU时间比比较所需的CPU时间多,故数据规模较大的时候,冒泡排序的效率更低。
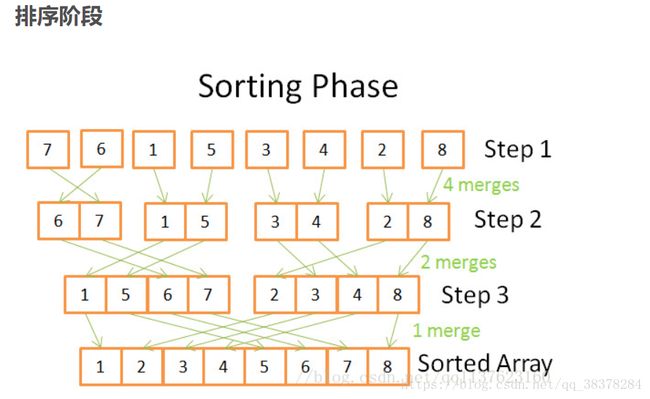
3.合并排序(merge_sort)
(1)原理: 合并排序法是采用分治法的一个典型应用,它将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

(3)复杂度分析:从上面的两个原理图可以知道,拆分阶段一共有log2(n)个步骤,而在合并阶段则需要对每一个步骤的两个子序列合并起来,即对n个元素进行排序,可以分析出其平均复杂度为 O(nlgn)。
(4)测试结果(数据规模从10000到60000):
![]()
结果分析:归并排序算法的时间复杂度为O(nlogn),由运行结果可知,其对于较大规模数据的排序效率很高。
4.快速排序(quick_sort)
(1)原理:通过一轮的排序将序列分割成独立的两部分,其中一部分序列的关键字均比另一部分关键字小。继续对长度较短的序列进行同样的分割,最后到达整体有序。在排序过程中,由于已经分开的两部分的元素不需要进行比较,故减少了比较次数,降低了排序时间。

(3)算法复杂度分析:
1)最优情况:排序n个元素,如果Partition每次都划分得很均匀,其递归树的深度就为 [log2n]+1,即仅需递归 log2n 次。第一次Partiation需要对整个数组扫描一遍,做n次比较,需要时间为T(n)。然后,获得的枢轴将数组一分为二,那么各自还需要T(n/2)的时间。这时的时间复杂度与合并排序相同,都是O(nlogn)。
2)最坏情况:当我们需要升序(降序)的时候,待排序的序列为逆序(正序),且每次划分只得到一个比上一次划分少一个记录的子序列,另一个为空。此时需要执行n‐1次递归调用,且第i次划分需要经过n‐i次关键字的比较才能找到第i个记录,,因此比较次数为

最终其时间复杂度为O(n^2)。
(4)测试结果(数据规模从10000到60000):
![]()
分析:快速排序算法是冒泡排序的优化,它具有最好的平均性能O(nlogn)。但是当基数值不能很好地分割数组,即基准值将数组分成一个子数组中有一个记录,而另一个子组组有 n -1 个记录时,下一次的子数组只比原来数组小1,这是快速排序的最差的情况。如果这种情况发生在每次划分过程中,那么快速排序就退化成了冒泡排序,其时间复杂度为O(n^2)。
5.直接插入排序(straight_insert)
(1)原理:插入即表示将一个新的数据插入到一个有序数组中,并继续保持有序。例如有一个长度为N的无序数组,进行N-1次的插入即能完成排序;第一次,数组第1个数认为是有序的数组,将数组第二个元素插入仅有1个有序的数组中;第二次,数组前两个元素组成有序的数组,将数组第三个元素插入由两个元素构成的有序数组中…第N-1次,数组前N-1个元素组成有序的数组,将数组的第N个元素插入由N-1个元素构成的有序数组中,则完成了整个插入排序。

(3)算法复杂度分析:
1)最好情况:如果是把 n 个元素的序列升序排列,且序列已经是升序排列了,在这种情况下,需要进行的比较操作需 n-1 次即可。
2)最坏情况就是,序列原本是降序排列,那么此时需要进行的比较共有 n*(n-1)/2 次。平均来说插入排序算法复杂度为 O(n2)。
(4)测试结果(数据规模从10000到60000):
![]()
分析:简单插入排序在最好情况下,需要比较n-1次,无需交换元素,时间复杂度为O(n);在最坏情况下,时间复杂度依然为O(n2)。但是在数组元素随机排列的情况下,插入排序还是要优于选择和冒泡两种排序的。
二.排序算法时间效率比较
(1)将先前五种排序算法在不同规模下的平均运行时间汇总,如下:
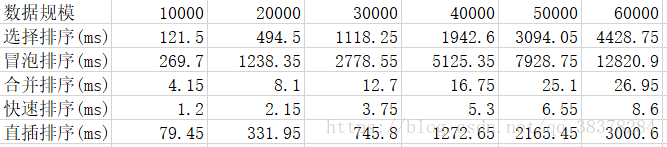
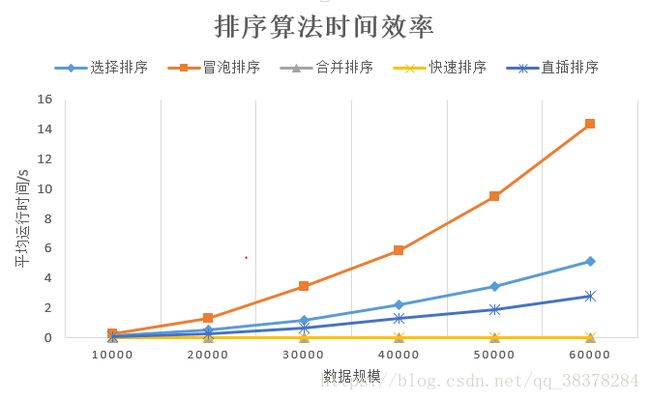
(2)性能分析:由折线图可以看出,快速排序与合并排序效率最好,插入排序次之,然后是选择排序,最后是冒泡排序的运行效率最差。
(3)由于合并排序与快速排序的最好时间都是O(nlogn),两者的运行效率都优于其他算法,为此单独来看看两者的运行效率的区别:

由此可知,快速排序的效率是优于合并排序的。虽然两者的时间复杂度都是O(nlogn),但是合并排序的空间复杂度为O(n),而快速排序的空间复杂度最好情况为O(logn)。
二.排序理论效率与实际效率分析比较
以输入规模为10000的数据运行时间为基准点,计算输入规模为其他值的理论运行时间。
(1) 选择排序


分析:
由上图可知实际效率与理论效率基本吻合,偏差甚微。当数据规模到达40000以上的时候,理论效率会略微小于实际效率,这是因为赋值操作随着n的增大而增大,并且在时间上体现出来。
(2) 冒泡排序


分析:
由上图发现实际效率与理论效率相差不小。这是因为赋值操作产生的误差随着数据规模的增加而越来远大,当数据规模达到万级以上的时候这个误差已经不能忽略不计。
(3) 合并排序

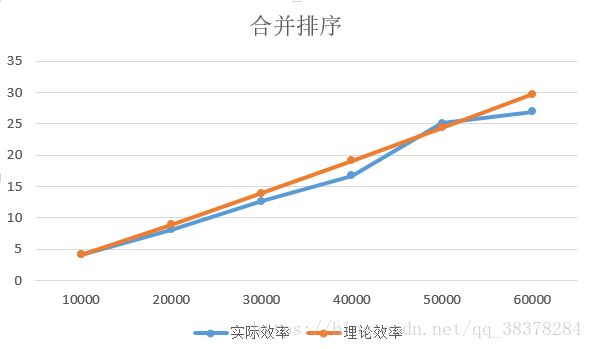
分析:
由上图发现,实际效率竟然有的时候可以比理论效率更好。这是因为将两个已经排好的子序列合并成一个有序的序列的时候,如果左子序列已经排好,那么可以直接将剩余的右子序列移动过去,而减少了循环和判断次数。
(4) 快速排序

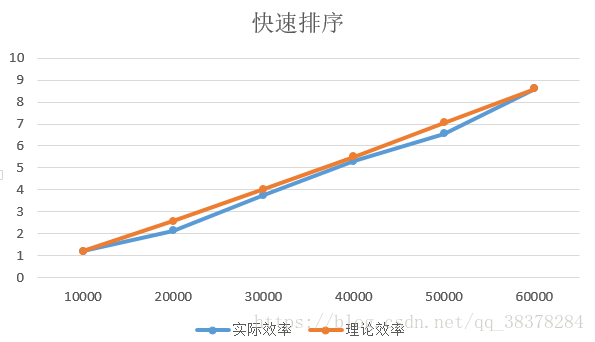
分析:
由上图快速排序的实际效率和理论效率虽然有偏差,但是可以忽略不计。造成偏差的主要原因是快速排序时间复杂度的最好情况与最坏情况分别为O(nlogn)和O(n^2),不同的数据规模,不同的样本,排序的情况自然有所不同,有偏差很正常。