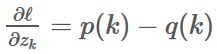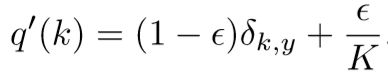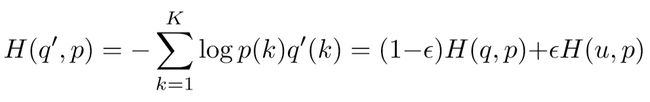Inceptionv3论文详解

原文地址：

https://arxiv.org/pdf/1512.00567.pdf

 

论文目标：

高效增大网络，即通过适当的分解卷积和有效的正则化尽可能有效地利用所增加的计算。

 

Inception网络的缺点分析：

1.Inception架构的复杂性使得更难以对网络进行更改。如果单纯地放大架构，大部分的计算收益可能会立即丢失（计算效率高的优势立即降下来）。

2.缺少一个关于Inception网络的设计决策的明确描述。这使得它更难以在适应新用例的同时保持其效率。例如，如果认为有必要增加一些Inception模型的能力，将滤波器组大小的数量加倍的简单变换将导致计算成本和参数数量增加4倍。这在许多实际情况下可能会被证明是禁止或不合理的，尤其是在相关收益适中的情况下。

 

卷积网络通用设计原则的尝试提出(以下原则的效用是推测性的)：

1.bottleneck(有信息丢失的操作类似下采样或者1*1的卷积)可以降维降低计算量，但是也会丢失信息，所以要合适地降，别降太猛丢信息了；

2.更高维度的特征表示，更稀疏，耦合更少，更好训练；

3.空间聚合可以通过低纬嵌入，不会导致网络表示能力的降低。例如在进行大尺寸的卷积（如3*3）之前，我们可以在空间聚合前先对输入信息进行降维处理，如果这些信号是容易压缩的，那么降维甚至可以加快学习速度。可能是因为通道间信息相关性比较高。

4.平衡好网络的深度和宽度。通过平衡网络每层滤波器的个数和网络的层数可以是网络达到最佳性能。增加网络的宽度和深度都会提升网络的性能，但是两者并行增加获得的性能提升是最大的。

 

Inception网络改进步骤：

1.卷积的大滤波器尺寸分解：

使用原因：

GoogLeNet网络[20]的大部分初始收益来源于大量地使用降维。这可以被视为以计算有效的方式分解卷积的特例。至于为什么这么做可以（不会大量丢失信息造成效果变差），因为在视觉网络中，相近激活层的输出是高度相关的，所以，激活可以在聚合之前被减少。

分解得到更小的卷积核：

利用卷积结构和平移不变性原则可以实现两个卷积串联对一个大卷积的替换。
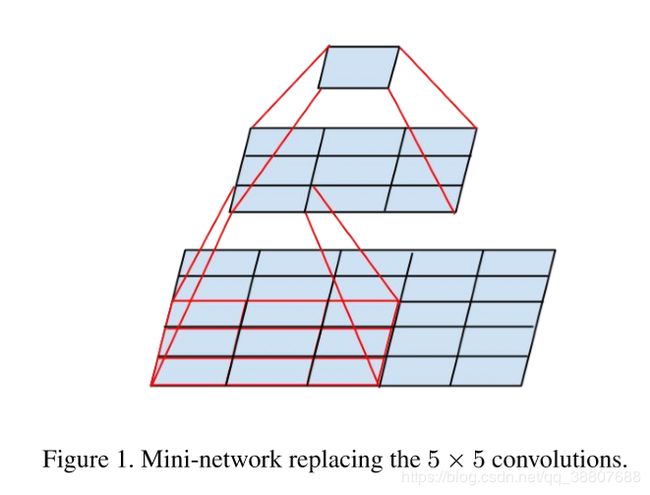
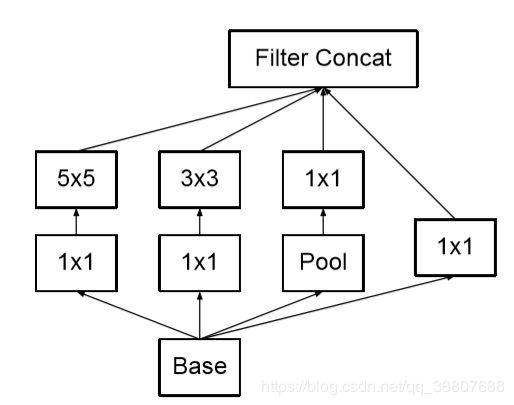
对5*5卷积的3*3替代：

Inception中对5*5卷积块的替换：

替换效果的分析：

替换后的好处：
通过相邻块之间共享权重(原来5*5个参数，现在3*3个参数，但是3*3个参数可以通过在5*5的区域内共享权重的滑动达到采集特征而又减小参数的目的)明显减少了参数数量。

替换的反思：
这样替换会不会导致任何表征力的丧失？
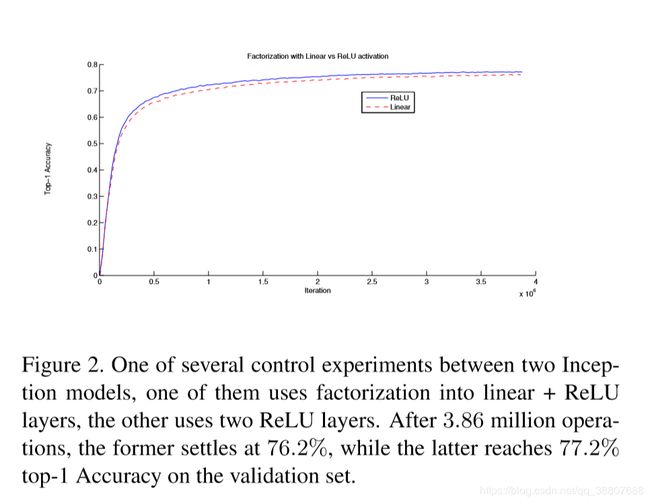
如果3*3对5*5的分解是一种线性关系的分解，那么我们分解之后的两个卷积层间使用的激活函数是不是保持线性激活更好？所以现在做实验看看到底分解的是不是线性关系：

结果表明，第一层使用线性激活函数反而有没Relu的效果好，所以可见分解的关系不是线性关系。

 

空间分解为不对称卷积：

思路由来：
分解3*3的卷积核有效果，那么继续往下分解成更小的呢？

使用不对称卷积：
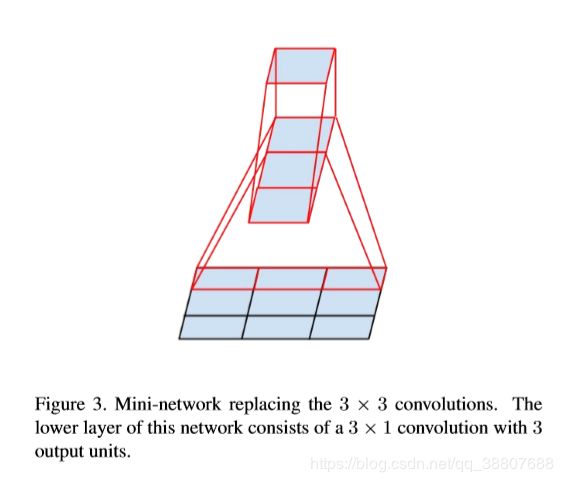
不对称卷积的分通过使用非对称卷积，可以做出甚至比2×2更好的效果，即n×1。例如使用3×1卷积后接一个1×3卷积，相当于以与3×3卷积相同的感受野滑动两层网络（参见图3）。如果输入和输出滤波器的数量相等，那么对于相同数量的输出滤波器，两层解决方案便宜33％。相比之下，将3×3卷积分解为两个2×2卷积表示仅节省了11％的计算量。所以，可以把卷积核分解到更小。

计算量分析：
一个5x5的图用一个3x3的模板去卷积,padding=SAME,stride=1,那卷积模板需要横向位移4次(即计算5次),纵向位移4次(同上),即横向纵向一共计算5x5=25次,每个模板是3x3也就是要计算9个数,一共就是25x9=225次。然后换成1x3和3x1两个模板去卷积,1x3需要横向计算5次,纵向计算5次,每次3个数,一共就是5x5x3=25x3=75,同理3x1模板也需要计算75次,即一共150次，225和150差33%（这个计算过程默认padding=same）。https://www.zhihu.com/question/270055683/answer/351817237

使用过程的一个注意点：
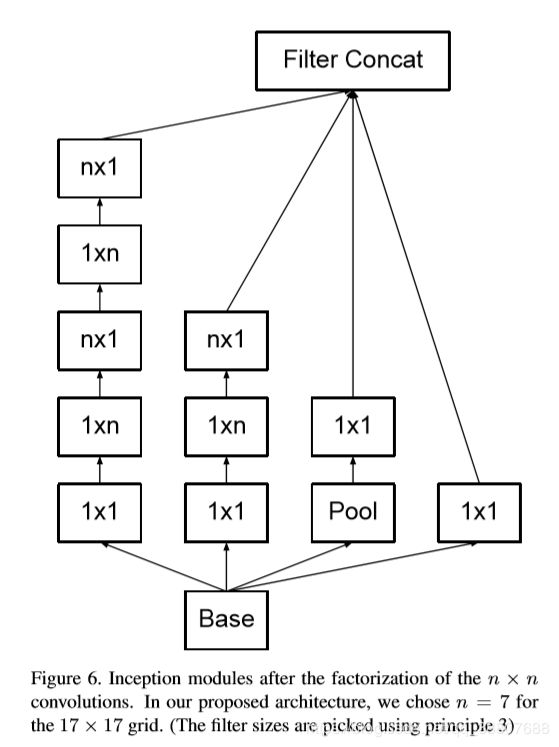
对中等Fm使用1×n卷积和后面接一个n×1卷积替换任何n×n卷积效果才比较好：
实际上，我们发现，采用这种分解在前面的层次上不能很好地工作，但是对于中等网格尺寸（在m×m特征图上，其中m范围在12到20之间），其给出了非常好的结果。在这个水平上，通过使用1×7卷积，然后是7×1卷积可以获得非常好的结果。

2.辅助分类器的使用（有进一步的发现）：

原来辅助分类器的作用是克服梯度消失与提供正则化。我们现在有趣的一点发现是辅助分类器的作用在训练的末期才开始显现出来：
辅助分类器在训练早期并没有导致改善收敛：在两个模型达到高精度之前，有无侧边网络的训练进度看起来几乎相同。接近训练结束，辅助分支网络开始超越没有任何分支的网络的准确性，达到了更高的稳定水平。

从发现的结果我们推测：
1.辅助分类器有助于演变低级特征的推断可能是不正确的
2.相反，我们认为辅助分类器起着正则化项的作用。由于如果侧分支是批标准化的[7]或具有丢弃层，则网络的主分类器性能更好。这也为推测批标准化作为正则化项给出了一个弱支持证据。

3.在不引入表征瓶颈的情况下减小网格尺寸(Fm的大小)

Inception结合传统方法：

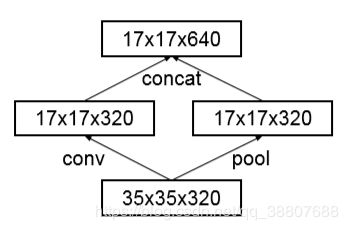
使用池化操作来缩减Fm网格大小。为了避免表征瓶颈，在应用最大池化或平均池化之前，需要扩展网络滤波器的激活维度。如下所示，例如，开始有一个带有k个滤波器的d×d网格，如果我们想要达到一个带有2k个滤波器的d/2×d/2网格，我们首先需要用2k个滤波器计算步长为1的卷积，然后应用一个额外的池化步骤。总体计算成本由在较大的网格上使用2d2k2次运算的昂贵卷积支配.

另一种减小运算量的做法如下，先进行池化，再进行维度扩展。因此导致主要运算量为2(d/2)2k2次运算.运算量是上面方法的四分之一。

当然，这种方法是更不可取的，因为它违反了原则1，引入了表征瓶颈，减弱了网络的表现力。

提出新的减小Fm网格大小的方法(降低计算成本的同时避免表征瓶颈)：

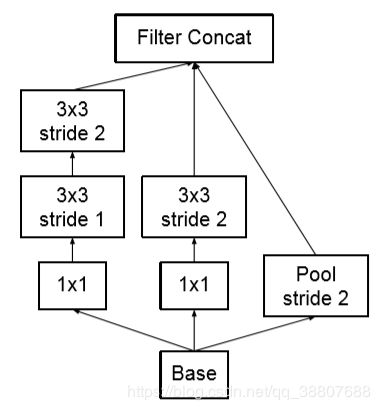
方法描述：
使用平行的步长为2的块，池化和卷积操作平行。达到减小网格与表征瓶颈的相互平衡。

另一种更直观的表示：

4.通过标签平滑进行模型正则化

标签平滑正则化理论：
(基本概念可以参考：http://cxsmarkchan.com/articles/ml-regularization-label-smoothing.html)

我们对单个样本计算每个标签的概率(这里，zi是对数单位或未归一化的对数概率)：

考虑这个训练样本在标签上的实际分布q(k|x)（相当于已知的标签y）,因此归一化后

为了简洁，我们不将p和q对样本x的依赖写出来。

如果我们用交叉熵定义样本损失的话，损失如下：

最小化交叉熵（前面有负号，所以是最大化标签的对数似然期望）等价于最大化标签对数似然期望，其中标签是根据它的实际分布q(k)选择的。交叉熵损失对于zk是可微的，因此可以用来进行深度模型的梯度训练。所以，梯度

它的范围在−1到1之间。

考虑单个真实标签y的例子，对于所有k≠y，有q(y)=1，q(k)=0。在这种情况下，最小化交叉熵等价于最大化正确标签的对数似然。对于一个特定的样本x，其标签为y，对于q(k)=δk,y，最大化其对数概率，δk,y为狄拉克δ函数，当且仅当k=y时，δ函数值为1，否则为0。如果对应实际标签的逻辑单元远大于其它的逻辑单元，那么对数概率会接近最大值（1）。

如果像上述这样表示损失(这也就是传统的交叉熵表示方法)，会两个缺点：

1.它可能导致过拟合：如果模型学习到对于每一个训练样本，分配所有概率到实际标签上，那么它不能保证泛化能力。
2.它鼓励最大的逻辑单元与所有其它逻辑单元之间的差距变大，与有界限的梯度∂ℓ/∂zk相结合，这会降低模型的适应能力。直观上讲这会发生，因为模型变得对它的预测过于自信。如若标签中有错误的训练标签，那这种自信将对模型的训练很不利。

标签平滑正则化理论的正式提出：
所以，我们提出了一个鼓励模型不那么自信的机制。如果目标是最大化训练标签的对数似然，那这个机制可能不是想要的，但它确实使模型正规化并使其更具适应性。

这个方法很简单。考虑标签u(k)的分布和平滑参数ϵ，与训练样本x相互独立。对于一个真实标签为y的训练样本，我们用

代替标签分布q(k|x)=δk,y。其由最初的实际分布q(k|x)和固定分布u(k)混合得到，它们的权重分别为1−ϵ和ϵ。这可以看作获得标签k的分布如下：首先，将其设置为真实标签k=y；其次，用分布u(k)中的采样和概率ϵ替代k。我们建议使用标签上的先验分布作为u(k)。在我们的实验中，我们使用了均匀分布u(k)=1/K，以便使得

我们将真实标签分布中的这种变化称为标签平滑正则化，或LSR。LSR实现了期望的目标，阻止了最大的逻辑单元变得比其它的逻辑单元更大。实际上，如果发生这种情况，则一个q(k)将接近1，而所有其它的将会接近0。这会导致q′(k)有一个大的交叉熵，因为不同于q(k)=δk,y，所有的q′(k)都有一个正的下界(这里主要指其他的非正确标签的q′(k))。

LSR的另一种解释可以通过考虑交叉熵来获得：

标签正则化效果：

在我们的K=1000类的ImageNet实验中，我们使用了u(k)=1/1000和ϵ=0.1。对于ILSVRC 2012，我们发现对于top-1错误率和top-5错误率，持续提高了大约0.2%。

 

最终的Inception V3架构：

相比Inception之前的版本，有如下更改：

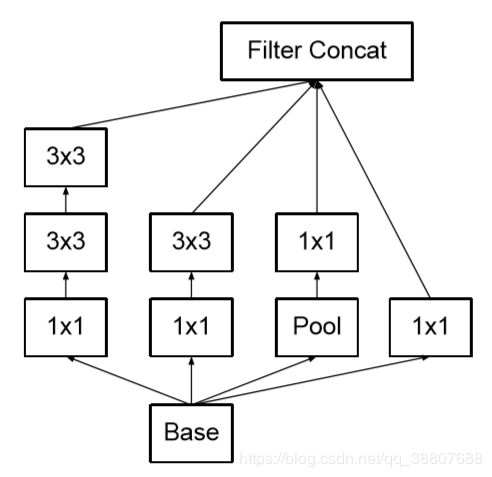
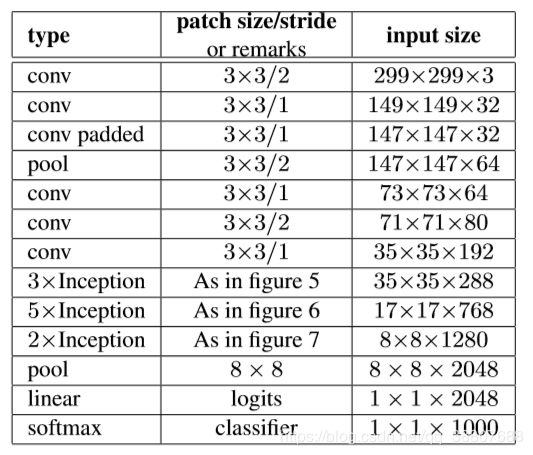
1.我们将传统的7×7卷积分解为3个3×3卷积
2.对于网络的Inception部分，我们在35×35处有3个传统的Inception模块，每个模块有288个滤波器。
3.使用第5节中描述的网格缩减技术，这将缩减为17×17的网格，具有768个滤波器。
4.这之后是图5所示的5个分解的Inception模块实例。使用图10所示的网格缩减技术，这被缩减为8×8×1280的网格。
5.在最粗糙的8×8级别，我们有两个如图6所示的Inception模块，每个块连接的输出滤波器组的大小为2048。

我们的网络深度是42层，但我们的计算成本仅比GoogLeNet高出约2.5倍，它仍比VGGNet要高效的多。

最后17×17层之上的辅助分类器。 侧头中的层的批标准化[7]导致top-1 0.4％的绝对收益

 

模型训练方法

1.TensorFlow[1]分布式机器学习系统
2.随机梯度方法训练
3.使用了50个副本，每个副本在一个NVidia Kepler GPU上运行
4.批处理大小为32，100个epoch
5.之前的实验使用动量方法[19]，衰减值为0.9，而我们最好的模型是用RMSProp 实现的，衰减值为0.9，ϵ=1.0。
6.使用0.045的学习率，每两个epoch以0.94的指数速率衰减
7.阈值为2.0的梯度裁剪被发现对于稳定训练是有用的，梯度截断可以一定程度上缓解梯度爆炸问题
具体参考：https://blog.csdn.net/guolindonggld/article/details/79547284
8.使用随时间计算的运行参数的平均值来执行模型评估。

 

模型测试：

1.低分辨率上模型的测试:

我们想要确定的一个问题是：

如果计算量保持不变，更高的输入分辨率会有多少帮助。一个简单方法是在较低分辨率输入的情况下减少前两层的步长，或者简单地移除网络的第一个池化层。

我们进行了下面三个实验：

1.步长为2，大小为299×299的感受野和最大池化。
2.步长为1，大小为151×151的感受野和最大池化。
3.步长为1，大小为79×79的感受野和第一层之后没有池化。

当感受野尺寸变化时，识别性能的比较，在每种情况下，网络都进行了训练，直到收敛，并在ImageNet ILSVRC 2012分类基准数据集的验证集上衡量其质量。

结果表明：

虽然分辨率较低的网络需要更长时间去训练，但最终结果却与较高分辨率网络的质量相当接近。

从结果可以感悟出：

对更小的对象使用专用的高成本低分辨率网络是一个不错的主意。

 

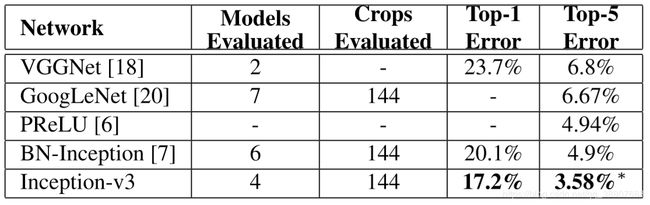
2.Inception V3的多裁剪图像和组合设置评估

我们将最后一行的模型称为真正的Inception-v3

模型组合评估结果，比较多模型，多裁剪图像的报告结果：

 

 

欢迎批评指正，讨论学习~
最近在github放了两份分类的代码，分别是用Tensorflow和Pytorch实现的，主要用于深度学习入门，学习Tensorflow和Pytorch搭建网络基本的操作。打算将各网络实现一下放入这两份代码中，有兴趣可以看一看，期待和大家一起维护更新。
代码地址：
Tensorflow实现分类网络
Pytorch实现分类网络