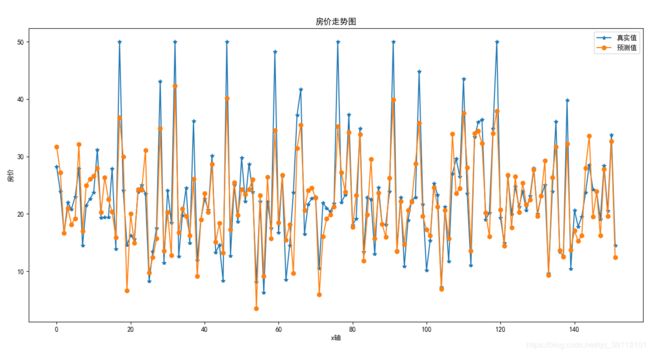
基于线性回归的波士顿房价预测
波士顿数据集在sklearn中自带,使用的时候引入就可以直接使用
from sklearn.datasets import load_boston#加载波士顿数据集
获取特征值、目标值和列名称
数据以字典的形式保存,获取的时候需要按照字典的方式提取数据
feature = boston['data'] #特征值 feature_names = boston['feature_names'] #特征值的列名称 target = boston['target'] #目标值
将特征值和目标值转化为df格式,给特征值和目标值加上列名称,并且拼接特征值和目标值,并且将结果保存到本地的excel文件中
#将波士顿房价数据保存到本地 #将特征值和目标值转化为df, df_feature= pd.DataFrame(feature,columns=feature_names) df_target= pd.DataFrame(target,columns=['MEDV']) #将特征值df与目标值df拼接,在进行保存 df_data = pd.concat((df_feature,df_target),axis=1) #index=False,去除行索引 df_data.to_excel('./boston.xlsx',index=False)
训练集测试集拆分
这个时候需要导入包来拆分训练集合测试集
from sklearn.model_selection import train_test_split#训练集测试集拆分拆分的返回值是:先特征值(先训练接,再测试集),再目标值(先训练接,再测试集)。
#拆分数据集,拆分成训练集与测试集,特征值与目标值 #测试集占30% #返回值--先特征值(先训练接,再测试集),再目标值(先训练接,再测试集) #准确率不一样是由于拆分的随机性 #random_state=1 固定拆分,设置为1的话会固定拆分,0的话就不是固定拆分 x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.3,random_state=1)
缺失值和异常值不存在,所以跳过
进行标准化
目标值是具体的房价,特征值是各个特征,特征值量级减小--w变大。目标值不需要标准化,特征值需要标准化。
先计算均值与标准差,再进行转化
stand = StandardScaler() #先计算均值与标准差,再进行转化 x_train = stand.fit_transform(x_train) x_test = stand.fit_transform(x_test)
线性模型构建的三种方式如下
正规方程求解的方程:正规方程求解的线性回归适用于特征不是特别多,不是特别复杂度的数据。
from sklearn.linear_model import LinearRegression #正规方程求解的方程#进行构建模型--线性模型 #正规方程求解的线性回归--特征不是特别多,不是特别复杂度的数据 #实例化数据 lr = LinearRegression() #训练数据 lr.fit(x_train,y_train) #预测数据 y_predict = lr.predict(x_test) # print(y_predict) #计算准确率 score = lr.score(x_test,y_test) #获取权重与偏置 weight = lr.coef_ bias = lr.intercept_ # show_res(y_test,y_predict) print(score) print(weight) print(bias)
SGD线性回归,随机梯度下降线性回归,sgd适用于特征较大,数据量较多的情况,进行自我学习需要设置学习率,默认学习率为0.01,想要更改学习率---learning_rate = 'constant'且eta0=‘要设置的学习率’,梯度方向不需要考虑,因为他是沿着损失减小的方向的,学习率过大会造成梯度爆炸,梯度爆炸出现在复杂的神经网络中,梯度爆炸是损失或准确率全部变成NAN类型,梯度也不能过小,如果过小,会造成原地打转,此时梯度消失,--损失不减小,一直那么大。
学习率如何设置?一般为0.1、0.01或0.001,不能过大或过小。
from sklearn.linear_model import SGDRegressor #SGD线性回归,随机梯度下降线性回归#sgd适用于特征较大,数据量较多的情况 #进行自我学习需要设置学习率 #实例化数据 sgd = SGDRegressor() #默认学习率为0.01 #想要更改学习率---learning_rate = 'constant' eta0=要设置的学习率 #梯度方向--不需要考虑,因为他是沿着损失减小的方向的 #学习率如何设置,0.1 0.01 0.001 不能过大或过小 #学习率过大会造成梯度爆炸,梯度爆炸出现在复杂的神经网络中,梯度爆炸是损失或准确率全部变成NAN类型 #也不能过小,如果过小,会造成原地打转,此时梯度消失,--损失不减小,一直那么大 #训练数据 sgd.fit(x_train,y_train) #预测数据 y_predict = sgd.predict(x_test) # print(y_predict) #计算准确率 score = sgd.score(x_test,y_test) #获取权重与偏置 weight = sgd.coef_ bias = sgd.intercept_ # show_res(y_test,y_predict) print(score) print(weight) print(bias)
线性回归+L2正则化(让某些特征值的权重趋于0),在小的数据集上效果会比LinearRegression效果好一些,正规方程求解的线性回归特征不是特别多,不是特别复杂度的数据 。
线性回归+L2正则化(让某些特征值的权重趋于0) --在小的数据集上效果会比LinearRegression效果好一些 正规方程求解的线性回归--特征不是特别多,不是特别复杂度的数据 实例化数据 rd = Ridge() #训练数据 rd.fit(x_train,y_train) #预测数据 y_predict = rd.predict(x_test) # print(y_predict) #计算准确率 score = rd.score(x_test,y_test) #获取权重与偏置 weight = rd.coef_ bias = rd.intercept_ # show_res(y_test,y_predict) print(score) print(weight) print(bias)
绘图代码如下
def show_res(y_test,y_predict): ''' 结果展示 :param y_test: 测试集目标值真实值 :param y_predict: 预测值 :return: ''' plt.rcParams['font.sans-serif'] = 'SimHei' plt.rcParams['axes.unicode_minus'] = False plt.figure() x = np.arange(0,len(y_predict)) plt.plot(x,y_test,marker='*') plt.plot(x,y_predict,marker='o') plt.title('房价预测与真实值的走势') plt.xlabel('x轴') plt.ylabel('房价') plt.legend(['真实值','预测值']) plt.show()
完整代码如下
import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import load_boston#加载波士顿数据集 from sklearn.model_selection import train_test_split#训练集测试集拆分 from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LinearRegression #正规方程求解的方程 from sklearn.linear_model import SGDRegressor #SGD线性回归,随机梯度下降线性回归 from sklearn.linear_model import Ridge #岭回归=线性回归+L2正则化 def show_res(y_test,y_predict): ''' 结果展示 :param y_test: 测试集目标值真实值 :param y_predict: 预测值 :return: ''' plt.rcParams['font.sans-serif'] = 'SimHei' plt.rcParams['axes.unicode_minus'] = False plt.figure() x = np.arange(0,len(y_predict)) plt.plot(x,y_test,marker='*') plt.plot(x,y_predict,marker='o') plt.title('房价预测与真实值的走势') plt.xlabel('x轴') plt.ylabel('房价') plt.legend(['真实值','预测值']) plt.show() #加载数据 boston = load_boston() # print(boston) # 数据以字典的形式保存,获取的时候需要按照字典的方式提取数据,获取特征值 feature = boston['data'] feature_names = boston['feature_names'] target = boston['target'] # print(feature.shape) # print(feature_names) # print(target.shape) #将波士顿房价数据保存到本地 #将特征值和目标值转化为df, # df_feature= pd.DataFrame(feature,columns=feature_names) # df_target= pd.DataFrame(target,columns=['MEDV']) # # #将特征值df与目标值df拼接,在进行保存 # df_data = pd.concat((df_feature,df_target),axis=1) # # df_data.to_excel('./boston.xlsx',index=False) #拆分数据集,拆分成训练集与测试集,特征值与目标值 #测试集占30% #返回值--先特征值(先训练接,再测试集),再目标值(先训练接,再测试集) #准确率不一样是由于拆分的随机性 #random_state=1 固定拆分,设置为1的话会固定拆分,0的话就不是固定拆分 x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.3,random_state=1) # print('拆分结果') # print('x_train:\n',x_train) # print('x_test:\n',x_test) # print('y_train:\n',y_train) # print('y_test:\n',y_test) #缺失值检测--没有缺失值 #检测异常值--没有异常值 #进行标准化--需要标准化 目标值是具体的房价,特征值是各个特征,--特征值量级减小--w变大 #目标值不需要标准化,特征值需要标准化 stand = StandardScaler() #先计算均值与标准差,再进行转化 x_train = stand.fit_transform(x_train) x_test = stand.fit_transform(x_test) # stand.fit(x_test) # x_test = stand.transform() #进行构建模型--线性模型 #正规方程求解的线性回归--特征不是特别多,不是特别复杂度的数据 #实例化数据 # lr = LinearRegression() # #训练数据 # lr.fit(x_train,y_train) # #预测数据 # y_predict = lr.predict(x_test) # # print(y_predict) # #计算准确率 # score = lr.score(x_test,y_test) # #获取权重与偏置 # weight = lr.coef_ # bias = lr.intercept_ # # show_res(y_test,y_predict) # print(score) # print(weight) # print(bias) #sgd适用于特征较大,数据量较多的情况 #进行自我学习需要设置学习率 #实例化数据 # sgd = SGDRegressor() #默认学习率为0.01 #想要更改学习率---learning_rate = 'constant' eta0=要设置的学习率 #梯度方向--不需要考虑,因为他是沿着损失减小的方向的 #学习率如何设置,0.1 0.01 0.001 不能过大或过小 #学习率过大会造成梯度爆炸,梯度爆炸出现在复杂的神经网络中,梯度爆炸是损失或准确率全部变成NAN类型 #也不能过小,如果过小,会造成原地打转,此时梯度消失,--损失不减小,一直那么大 #训练数据 # sgd.fit(x_train,y_train) # #预测数据 # y_predict = sgd.predict(x_test) # # print(y_predict) # #计算准确率 # score = sgd.score(x_test,y_test) # #获取权重与偏置 # weight = sgd.coef_ # bias = sgd.intercept_ # # show_res(y_test,y_predict) # print(score) # print(weight) # print(bias) # ++++++++++线性回归+L2正则化(让某些特征值的权重趋于0) --在小的数据集上效果会比LinearRegression效果好一些 # 正规方程求解的线性回归--特征不是特别多,不是特别复杂度的数据 # 实例化数据 rd = Ridge() #训练数据 rd.fit(x_train,y_train) #预测数据 y_predict = rd.predict(x_test) # print(y_predict) #计算准确率 score = rd.score(x_test,y_test) #获取权重与偏置 weight = rd.coef_ bias = rd.intercept_ # show_res(y_test,y_predict) print(score) print(weight) print(bias)