【数据结构与算法】
递归法
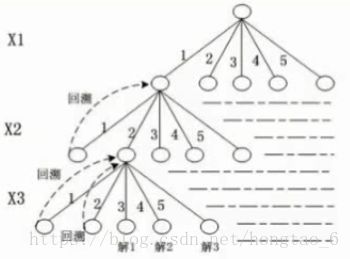
设法将问题分解成一些规模较小的问题,然后从这些小问题的解方便地构造出大问题的解,并且这些规模较小的问题也能采用同样的分解方法和综合方法。递推阶段,把复杂问题的求解推到较简单的问题求解上;回归阶段:获得最简单情况的解后逐级返回,获得稍复杂问题的解。典型用法是菲波那切数列。
通俗讲,递归就是在程序运行的过程中调用自己。如菲波那切数列:
F 0 =0,F 1 =1,F n =F n−1 +F n−2
int F(int n)
{
if(n==0) return 0;
if(n==1) return 1;
if(n>1) return F(n-1)+F(n-2);
}
分治法
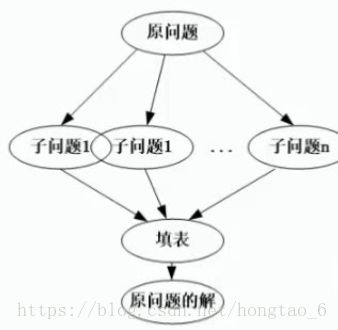
思想:将一个规模较大的问题,分解为一些规模较小的子问题,这些子问题相互独立且与原问题形式相同,递归地解决这些子问题,让后将各子问题的解合并得到原问题的解。步骤:分解,解决,合并
特点:
该问题可以分解为若干规模较小的相同问题
问题的规模缩小到一定的程度可以容易地解决
分解出的子问题的解可以合并为该问题的解
分解出的各个子问题相互独立
二分查找
int Binary_Search(L,a,b,x)
{
if(a>b) return -1;
else
{
m=(a+b)/2;
if(x == L[m]) return m;
else if (x>L[m])
return Binary_Search(L,m+1,b,x);
else
return Binary_Search(L,a,m-1,x);
}
}
回溯法
回溯法是一种深度优先的选优搜索法,按选优条件向前搜做,以达到目标。但当搜索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择。这种走不通就退回去再走的技术就是回溯法。
试探部分:扩大规模,满足除规模之外的所有条件,则扩大规模
回溯部分:缩小规模,当前规模解不是合法解时回溯,求完一个解要求下一个解时也要回溯。
典型问题:迷宫问题,N皇后问题
n皇后问题:在n×n格的棋盘上放置n个皇后,任何2个皇后不放在同一行或同一列或同一斜线上。
贪心法
总是做出在当前来说是最好的选择,而并不从整体上加以考虑,它所做的每步选择只是当前步骤的局部最优选择,但从整体来说不一定是最优的选择。由于它不必为了寻找最优解而穷尽所有可能解,因此其耗费时间少,一般可以快速得到满意的解,但得不到最优解。
典型问题:背包问题:有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
动态规划法
在求解问题中,对于每一步决策,列出各种可能的局部解,再依据某种判定条件,舍弃那些肯定不能得到的局部最优解,在每一步都经过筛选,以每一步都是最优解来保证全局是最优解。
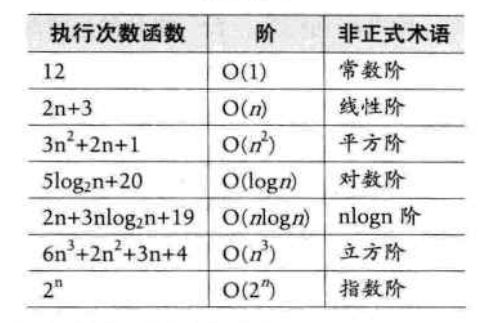
时间复杂度计算
常数阶
int sum=0,n=1000;
sum=(1+n)*n/2;
printf("%d",sum);
以上是顺序结构的时间复杂度,这个算法的运行次数函数是f(n)=3。根据上面的方法,第一部就是把常数改成1,。在保留最高阶时发现,它根本没有最高阶项,所以它的时间复杂度是O(1)。
对于分支结构而言,无论是真,还是假,执行的次数都是恒定的,不会随着n的变化而发生变化,所以单纯的分支结构(不包含在循环结构中),其时间复杂度也是O(1)。
线性阶
要分析算法的复杂度,关键就是要分析循环结构的运行情况。
int i;
for(i=0;i上面的代码,它的时间复杂度是O(n),因为循环体中的代码需要执行n次。
对数阶
int count=1;
while (count < n)
{
count=count * 2;
int sum=0,n=1000;
sum=(1+n)*n/2;
printf("%d",sum);
}
由于每次count乘以2之后,就距离n更近了一分。也就是说,有多少个2相乘后大于n,则会退出循环。又2x=n 得到x=log2n。所以找个循环的时间复杂度为O(logn)。
平方阶
下面的代码是一个循环嵌套,根据上面的分析,内循环的时间复杂度为O(n)
int i ,j;
for(i=0;i对于外部的循环,不过是内部的循环又循环了n次,所以这段代码的时间复杂度为O(n2)。
如果外循环的次数改成了m,即
int i ,j;
for(i=0;i那么时间复杂度就是O(m×n)所以总结得出,循环的时间复杂度等于循环体的复杂度乘以该循环的运行的次数。
常见的时间复杂度
常见的数量级大小:O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n ^ 3)<O(2^n)<O(n!)
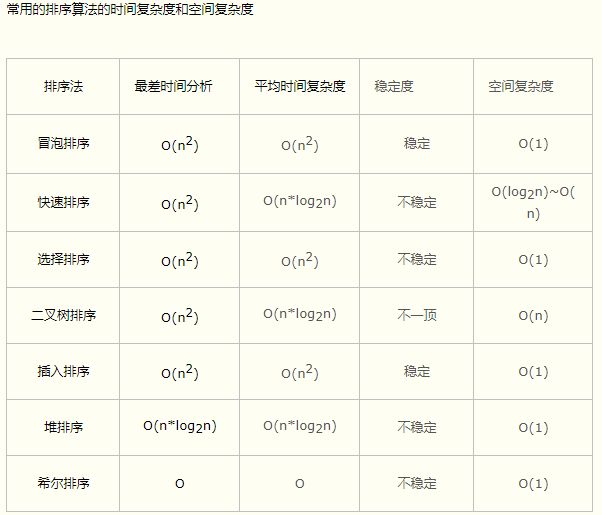
排序算法
冒泡排序
基本思想:两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
以升序冒泡为例:每趟排序过程中通过两两比较相邻元素,将小的数字放到前面,大的数字放到后面。
快速排序(Quick Sort)
通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分关键字小,则分别对这两部分继续进行排序,直到整个序列有序。
一次划分过程,以第一个数字49位基准:
初始关键字 [49 38 65 97 76 13 27 49]
一趟排序之后 [27 38 13] 49 [76 97 65 49]
二趟排序之后 [13] 27 [38] 49 [49 65]76 [97]
三趟排序之后 13 27 38 49 49 [65]76 97
最后的排序结果 13 27 38 49 49 65 76 97
简单选择排序
基本思想:
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。
2.排序过程:
【示例】:
初始关键字 [49 38 65 97 76 13 27 49]
第一趟排序后 13 [38 65 97 76 49 27 49]
第二趟排序后 13 27 [65 97 76 49 38 49]
第三趟排序后 13 27 38 [97 76 49 65 49]
第四趟排序后 13 27 38 49 [49 97 65 76]
第五趟排序后 13 27 38 49 49 [97 97 76]
第六趟排序后 13 27 38 49 49 76 [76 97]
第七趟排序后 13 27 38 49 49 76 76 [ 97]
最后排序结果 13 27 38 49 49 76 76 97
堆排序(Heap Sort)
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子
该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
**大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] **
**小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] **
堆排序的基本思想是:
将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换,此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了
直接插入排序(Insertion Sort)
基本思想:
每次将一个待排序的数据元素,插入到前面已经排好序的数列中的适当位置,使数列依然有序;直到待排序数据元素全部插入完为止。排序过程:
【示例】:
[初始关键字] [49] 38 65 97 76 13 27 49
J=2(38) [38 49] 65 97 76 13 27 49
J=3(65) [38 49 65] 97 76 13 27 49
J=4(97) [38 49 65 97] 76 13 27 49
J=5(76) [38 49 65 76 97] 13 27 49
J=6(13) [13 38 49 65 76 97] 27 49
J=7(27) [13 27 38 49 65 76 97] 49
J=8(49) [13 27 38 49 49 65 76 97]
希尔排序
1.排序思想:
先 取一个小于n的证书d1作为第一个增量,把文件的全部记录分成d1组。所有距离为d1的倍数的记录放在同一组中。先在各组内进行直接插入排序,然后取第二 个增量d2
希尔排序算法通过设置一个间隔,对同样间隔的数的集合进行插入排序,此数集合中的元素
移位的长度是以间隔的长度为准,这样就实现了大步位移。但是最后需要对元素集合进行一次直接插入排序,所以
最后的间隔一定是1。
下面举一个例子:
第一趟希尔排序,间隔为4
第二趟排序:间隔是2
第三趟 间隔为1,即 直接插入排序法:
有人问,这个间隔怎么确定,这是个数学难题,至今没有解答。但是通过大量的实验,还是有个经验值。
归并排序
1.排序思想:
设两个有序的子文件(相当于输入堆)放在同一向量中相邻的位置上:R[low..m],R[m+1..high],先将它们合并到一个局部的暂存向量R1(相当于输出堆)中,待合并完成后将R1复制回R[low..high]中。
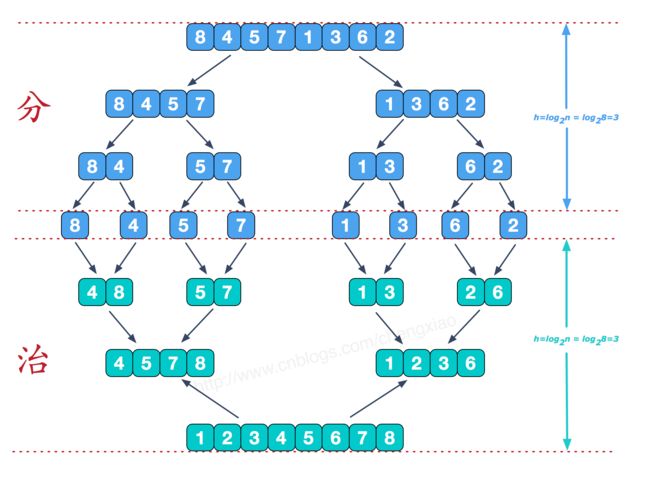
排序过程
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
基数排序
1.排序思想:
具体做法是:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列
2.排序过程
基数排序图文说明
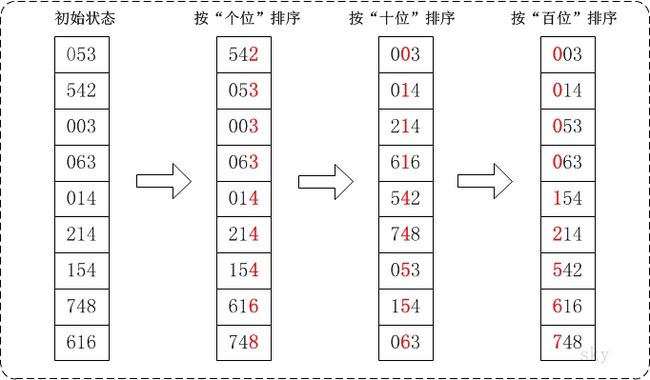
通过基数排序对数组{53, 3, 542, 748, 14, 214, 154, 63, 616},它的示意图如下:
在上图中,首先将所有待比较树脂统一为统一位数长度,接着从最低位开始,依次进行排序。
1. 按照个位数进行排序。
2. 按照十位数进行排序。
3. 按照百位数进行排序。
排序后,数列就变成了一个有序序列。
查找算法
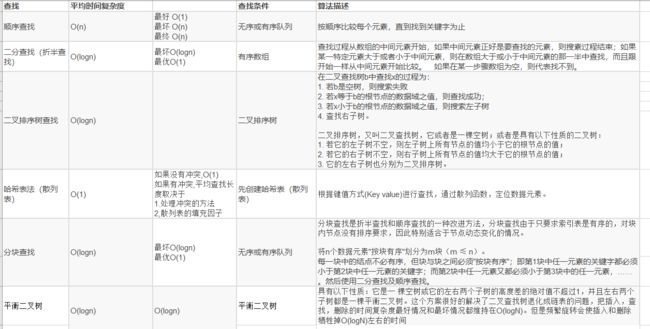
顺序查找
适合对象——无序或有序队列
(1)思想:逐个比较,直到找到或者查找失败。
(2)时间复杂度:T(n) = O(n)。
(3)空间复杂度:S(n) = O(n)。
折半查找(二分查找)
二分查找要求序列本身是有序的。因此对于无序的序列,我们要先对其进行排序。现在我们手头有一有序序列:
array[10] = {2,4,5,7,,8,9,13,23,34,45},则二分查找的过程为:
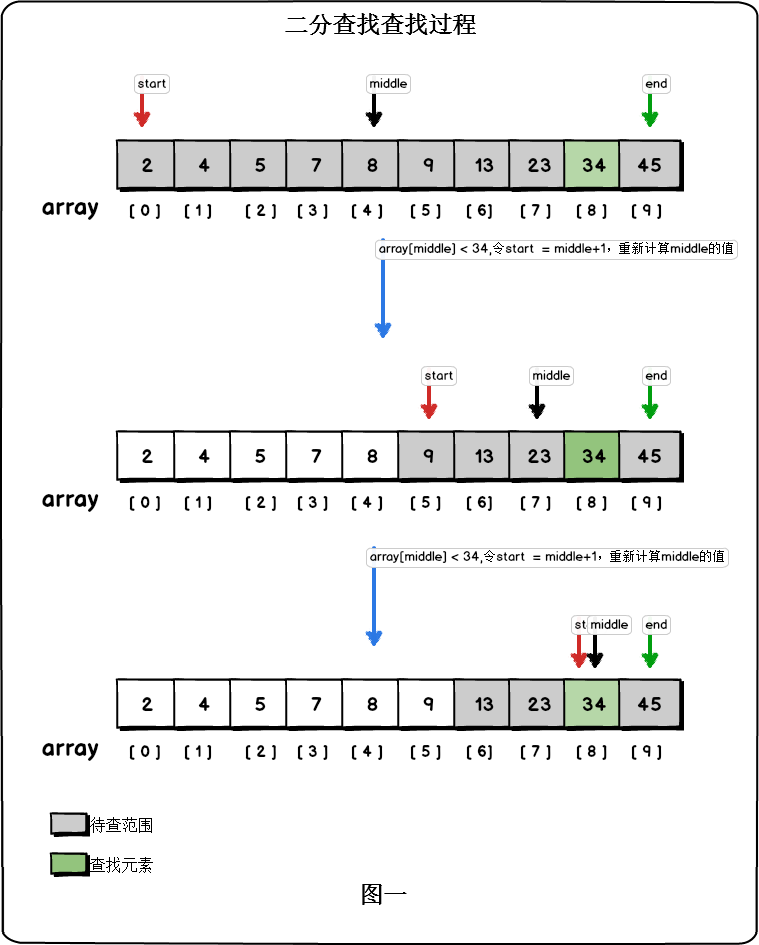
- 设置三个索引:start指向数组待查范围的起始元素,end指向数组待查范围的最后一个元素,middle=(start+end)/2。开始时待查范围为整个数组。
- 比较array[middle]与查找元素的大小关系:
- 如果array[middle]等于查找元素,则查找成功
- 如果array[middle]大于查找元素,则说明待查元素在数组的前半部分,此时缩小待查范围,令end = middle-1
- 如果array[middle]小于查找元素,则说明待查元素在数组的后半部分,此时缩小待查范围,令start = middle +1
- 重复执行前面两步,直到array[middle ] 等于查找元素则查找成功或start>end查找失败。
现在我们在数组{2,4,5,7,,8,9,13,23,34,45}中查找元素23,过程如图:
https://www.cnblogs.com/maybe2030/p/4715035.html
https://blog.csdn.net/cc1258000/article/details/79113211