复合映射
对于X,Y和Z三个集合,存在映射f,g和h
其中h可以表示为先f后g的复合映射,所以复合映射h可以表示为下面的形式,注意书写的顺序和映射复合的顺序相反。
流形(Manifold)
粗略的说,一个拓扑空间(Topological Space)再加上一个微分结构(Differentiable structure),称为流形(Manifold)。
开覆盖(Open Cover)
假定有一个拓扑空间M,存在一个由M上的若干开集(Open Set)组成的集合
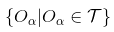
如果下式成立,则说上面这个是M的一个 开覆盖(Open Cover)

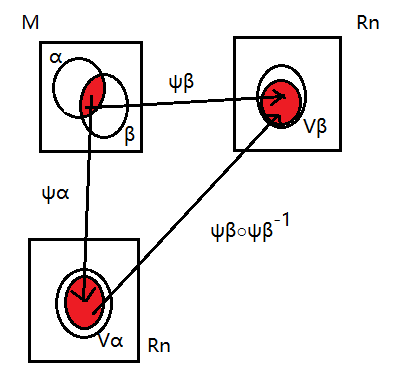
如果M上存在一个开覆盖,并且满足下面两个条件,则称M为一个n维的流形(Manifold)。
-
对于这个开覆盖中的任意一个开集Oα,存在一个从Oα到拓扑空间Rn上的某个开子集的同胚映射。(注意:Rn的拓扑结构在没有特殊声明的时候取通常拓扑(Usual topology),即可表示为开球之并的子集的集合)
-
对于开集Oα和开集Oβ,如果它们的交集不为空,则从Vα到Vβ上的复合映射的无限阶连续(任意阶导函数存在且连续)。
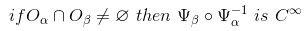
流形(Manifold)的维数是由映射ψ决定的,ψ将一个开集映射到一个几维的空间上,流形的维数就是几。
对于条件二,需要特别注意这个条件中映射的原像和像的范围。
第一个条件使得一个n维的流形(Manifold)的局部上看起来像一个Rn。
第二个条件保证了不同的开集之间的相容性,又叫做相容性条件(Compatibility condition)。
图/坐标系&图册(Chart/Coordinate System& Atlas)
对于M上的某个点,通过ψ映射得到了Rn上的一组数(x1,...,xn),这一组数称作这个点在ψ映射下对应的自然坐标。
对于M中红色区域中的点,在ψα和ψβ的映射下得到了(x1,...,xn),(x1',...,xn')两个不同的自然坐标,而这两个不同的自然坐标可以通过之前提到的复合映射进行变换,这就是所谓的坐标变换(Coordinate transformation)。
一般将流型上的某个开集O和其对应的映射ψ称作一个坐标系(Coordinate system),或者图(Chart),记作(O, ψ)。
若干图(Chart)的集合称做图册(Atlas),记作{ (O1, ψ1), ..., (On, ψn) }。
例子
给定R2上的一个拓扑空间 M = R2
- 寻找一个最简单的开覆盖:O1 = R2。
- 寻找一个最简单的同胚映射:ψ1 : R2 -> R2(恒等映射)
则M是一个2维流形,其图册为{ (O1, ψ1) }。
可以发现在上面的例子中,O1在映射ψ1下的坐标就是普通的直角坐标。
通过在开覆盖中给定其它满足条件的同胚映射,可以得到不同的坐标系(Coordinate system)或者图(Chart)。如果要使用极坐标来表示2维流型上的某个点,只需要按照上面说的找到其相应的映射即可。
给定R2上的一个拓扑空间S
可以按照下面的方式划分不同的 坐标系(Coordinate system)或 图(Chart)
由于图中四个相交的部分都等效,可以取其中一个加以证明,如黄色和绿色相交的地方。黄色区域的点在该坐标系下的坐标的值为该点在R2下自然坐标的横坐标,即x,同理绿色区域的点在其坐标系下的坐标为y。
对于一个从黄色区域对应的坐标系到绿色区域的坐标变换,其表达式为
显然上式无限阶连续(任意阶导函数存在且连续)
则M是一个1维流形,其图册为{ (O1, ψ1), (O2, ψ2), (O3, ψ3), (O4, ψ4) }。
图册(Atlas)
对于一个拓扑空间M,定义了两个不同的图册{ (O1, ψ1) }和{ (O2, ψ2) }。
当这两个图册不相容(O1和O2的交集不为空,并且从O1到O2的复合映射不是无限阶连续),这个时候就在同一个拓扑空间上定义了两个不同流形。
一开始谈流形的时候说过:一个拓扑空间再加上一个微分结构,称为流形。那么对于这两个流形,它们的拓扑结构是相同,不同的是它们微分结构。
而当这两个图册相容的时候,可以把这两个图册合并为一个更大的图册{ (O1, ψ1), (O2, ψ2) },这样3个图册定义出来流形的是一样的。为了方便,一般定义一个流形都取最大的图册。
流形间映射
假定存在一个从流形M到流形M’上的映射f,根据流形的定义,分别选定它们开覆盖上的开集O和O',且它们分别存在从自身到对应维度的拓扑空间Rn和Rn'上的某个开子集的同胚映射,如下图所示
观察图中的映射关系,可以发现映射f是ψ、g和ψ'逆映射的复合,根据流形的定义可以知道ψ和ψ'为同胚映射,所以要看映射f的连续性,只需要看映射g的连续性,如果g是无限阶连续的,则f也是无限阶连续的。
之前提到,两个拓扑空间的映射如果是One to one和onto,并且正反映射都是C0连续的,则称它们是同胚的。
同样地,两个流形之间的映射如果是One to one和onto,并且正反映射都是无限阶连续的,则称它们是微分同胚(Diffeomorphism)的。
标量场 & 函数(Scaler Field & Function)
假定存在一个从流形M到实数域R上的映射f,则称映射f为一个函数(Function)或者标量场(Scaler field)。
需要特别注意,这里的函数和我们之前学的函数是不一样的。
以前我们考虑一个n元函数需要给定一个n元的自变量,换句话说就是要给定一个坐标,而对于流形M上的同一个点,由于给定的坐标系或图不同,得到的坐标也不同。不同的坐标通过函数得到的函数值相同,所以这几个函数的函数关系也不同。
所以,对于之前理解的函数,他是依赖于坐标系或图,它是相对的。而这里的我们所提到的函数是不依赖于具体坐标系,它是绝对的。
所以为了防止混淆,把这个从流形M到实数域R上的映射f称作标量场更加合适。
开子集&闭子集
如果一个子集是开子集(Open Subset),那么它的补集就是闭子集(Closed Subset)。
一个集既可以是开的,也可以是闭的,还能是不开不闭和即开又闭的。
全集是开子集,全集的补集是空子集,所以空集是闭子集,而空集又是开子集,所以空集即开又闭,反之同理可以得到全集也是既开又闭的。
连通性(Connectivity)
如果一个拓扑空间的既开又闭的子集只有两个,则称它是连通的(Connected)。
还有一个和上面连通性定义比较像的定义:对于一个拓扑空间内的任意两点,如果它们都能够被处于该拓扑空间内部的一条曲线连接,则称它是弧连通。
这两个定义本身是有一定区别的,不过在研究流形的时候它们是没有区别的。