前言
最近在研读OkHttp源码,发现它的Dispatcher分发器使用了ArrayDeque数据集合,这个集合类是java.util里提供的双端队列/栈,非线程安全,但是性能很好,非常值得研究一下。
基本设计
我们先整体推测一下ArrayDeque的设计思路。
功能
每一种集合类的具体功能,基本上都是增/删/改/查四大项,ArrayDeque也不例外,只不过它更贴近于栈的功能,主要操作栈顶和栈底的数据,对于栈中的数据,只有delete一个函数。
问题
Java中一般只有两种基础的数据容器,数组或链表。数组排列紧密、下标查找快、中间插入慢;链表排列稀疏、查找慢,中间插入快。对于栈结构来说,采用数组更具优势,ArrayDeque也是采用了数组来作为基本数据容器,也需要处理数组扩容问题。
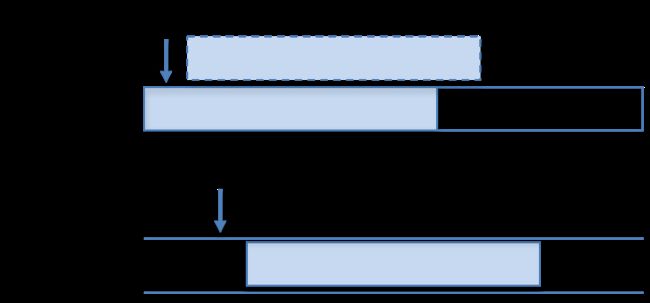
不过,传统的数组都是线性数组,向尾部添加数据固然很方便,但是向中间添加数据的话,就需要挪动插入点之后的所有数据,如果向头部添加数据的话,整个数组都要挪一遍,虽然Java提供了Native函数System.arrayCopy来提升效率,但是对内存的操作是不可避免的。
循环数组
为了提高效率,ArrayDeque采用了循环数组的设计,也就是说虽然基础容器是一个普通的数组(默认容量16),但是在逻辑上,这个数组没有固定的开头或结尾,既可以直接向尾部添加数据,也可以直接向头部之前添加数据,不需要大面积地移动数据。
逻辑上的概念大概是这样的:
具体实现及优化
循环数组在概念上没有左右边界,但是Java并没有这样的数组,Java只能提供固定大小的数组,这样的话,如何实现循环数组就转变为如何利用固定数组实现循环数组。
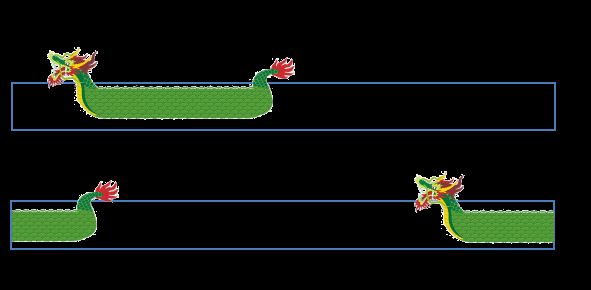
相对于线性数组,循环数组是连续的,但是数组的头和尾可能在任何位置,所以循环数组在真实数据中的映射大概是这样:
在逻辑上,队首总是在左边,队尾总是在右边,但是如果持续向队首插入数据,就很容易把队首”顶“出物理容器的左边界,”顶“进物理容器的右侧。
这时候,我们可以看到,循环数组在物理数组中最大的问题是, 很多时候,逻辑上连续,但物理上被分成了两截。
所以,ArrayDeque需要针对以下操作,做特殊处理:
1.添加/删除头
主要判断头的新位置在左侧还是右侧。
先看添加:
head的新位置一定是head-1,如果得到的结果为-1,就需要挪到右侧,也就是物理数组中的最后一个位置length-1。
如果让我们自己来写,可能是这样写:
if(head-1<0){
head=elements.length -1;
}else{
head=head-1;
}
elements[head]=e;
事实上,ArrayDeque使用了更精妙的实现,他用一步位与运算实现了这个功能:
elements[head = (head - 1) & (elements.length - 1)] = e;
这行代码具体什么意思呢?
当head-1为-1时,实际上是11111111&00001111,结果是00001111,也就是物理数组的尾部15;
当head-1为较小的值如3时,实际上是00000011&00001111,结果是00000011,还是3。
当head增长如head+1超过物理数组长度如16时,实际上是00010000&00001111,结果是00000000,也就是0,这样就回到了物理数组的头部。
所以,位与运算可以很轻松地实现把数据控制在某个范围内。
回过头来,我们再看删除头的代码:
elements[h] = null; // Must null out slot
head = (h + 1) & (elements.length - 1);
先清空数据,然后移动head位置,也是用位与运算实现的。
位运算本来就非常高效,ArrayDeque的这种写法,更是用一行代码覆盖了函数中的所有场景,非常精妙。
2.添加/删除尾
主要判断尾的新位置在左侧还是右侧,具体操作和上一步添加/删除头类似。
3.删除中间某个数据
删除中间元素时,即使是循环数组,也需要批量移动数组元素了,所以删除中间元素实际上面临三个问题,一是需要在左侧或右侧删除,二是需要挪动头或尾,三是优化需要,尽量少得移动数组元素。
ArrayDeque实际上是先从第三个问题入手的,先判断中间元素里head近还是离tail近,然后移动较近的那一端。
不过,较近的一端只是逻辑上较近,物理数组上,可能被分成了两截,这就需要做两次数组元素的批量移动。
//ArrayDeque源码(部分情况)
System.arraycopy(elements, 0, elements, 1, i);
elements[0] = elements[mask];
System.arraycopy(elements, h, elements, h + 1, mask - h);
4.计算队列长度,如果物理上不连续,需要特别计算真正的数据。
如果让我们自己写,可能也是分条件判断,分别计算两截的数据。
ArrayDeque又使用了位与运算:
return (tail - head) & (elements.length - 1);
也是只有一行,当物理上被分为两截时,tail-head会是负数,整个操作相当于取模运算,例如,当tail为3,head为14,物理数组长度16时,运算的就是11110101&00001111,值为00000101,也就是5。
5.复制一个线性数组toArray
从基本操作上,如果物理上不连续,先复制右侧,再补上左侧。
toArray的问题在于新数组的长度是动态的,为了生成大小刚好的新数组,ArrayDeque使用了Arrays工具类来实现这个特定长度的数组,并同时实现对head一侧数据的复制:
boolean wrap = (tail < head);
int end = wrap ? tail + elements.length : tail;
Object[] a = Arrays.copyOfRange(elements, head, end);
if (wrap)
System.arraycopy(elements, 0, a, elements.length - head, tail);
这样的话,如果物理空间连续,就直接复制完成;
但如果物理空间不连续,第一次Arrays.copyOfRange需要保证一次性生成足够的物理空间,所以end的值不能是length(否则长度就只有length-head这么长),而应该是tail+length。
6.空间扩容。
数据容器的扩容其实可以分解为两个问题,一是何时开始扩容,二是旧数组数据的复制。
对于何时开始扩容的问题,为了减少检查的次数,ArrayDeque采用了对head和tail是否重合的检查,只要tail和head不重合,就说明tail后面/head前面还有空间,所以只要在添加头/尾时检查head==tail即可。
对于旧数组数据的复制,空间扩容和问题和toArray有些类似,不同的是新数组的长度是可知的(2倍),所以可以直接new一个定长的数组,这样就不需要Array.copyOfRange函数,可以统一使用System.arrayCopy:
Object[] a = new Object[newCapacity];
System.arraycopy(elements, p, a, 0, r);
System.arraycopy(elements, 0, a, r, p);
其他
相比ArrayList,我们可以看到ArrayDeque大量减少了System.arrayCopy的使用,只在delete、clone、扩容和toArray函数中使用了这个函数,其他操作中都不需要大量移动数组元素,这也可以说明ArrayDeque这个数据集合的性能非常优良。
参考
Java ArrayDeque源码剖析