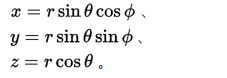我相信,很多人看到这个都是对google-s2有了解的,所以我在这里废话就不多说了,直接进入正题。
首先我们先看下目前都有什么资源
(1)GO源码:github.com/golang/geo
(2)java源码:github.com/google/s2-geometry-library-java
(3)唯一的pdf:pan.baidu.com/s/1gfxJB0J
然后我们理解一个概念:希尔伯特曲线(能够连续的把平面填满)
我们可以直观的看到该曲线到底是什么,不理解的去
维基百科
转转吧。
下面,让我们直观的感受一下,google-s2是如何把空间地理位置进行编码的,如何映射到一位空间的编码上的:bit-player.org/extras/hilbert/hilbert-mapping.html
请打开连接,随便点点吧,你会感觉很神奇。
不用怀疑了,你猜对了,原图都在这里:blog.christianperone.com/2015/08/googles-s2-geometry-on-the-sphere-cells-and-hilbert-curve/
到这点,我觉得是时候你去拜读一下这个连接了。
到现在,也许会有人问,为什么不用geohash而搞这玩意干啥?
你可以到这里看一下是为什么:www.tuicool.com/articles/UnEZvm
Why not Geohash?
(1)Geohash is a great solution to perform geo coordinates queries but the way it works can sometimes be an issue with your data.
(2)Remember geohashes are cells of 12 different widths from 5000km to 3.7cm, when you perform a lookup around a position, if your position is close to a cell’s edge you could miss some points from the adjacent cell, that’s why you have to query for the 8 neightbour cells, it means 9 range queries into your DB to find all the closest points from your location.
(3)If your lookup does not fit in level439km by 19.5km, the next level is 156km by 156km!
(4)The query is not performed around your coordinates, you search for the cell you are in then you query for the adjacent cells at the same level/radius, based on your needs, it means it works very approximately and you can only perform ‘circles’ lookup around the cell you are in.
(5)The most precise geohash needs 12 bytes storage.
(6)-90 +90 and +180 -180, -0 +0 are not sides by sides prefixes.
Why S2?
(1)S2 cells have a level ranging from30~0.7cm² to0~85,000,000km².
(2)S2 cells are encoded on an uint64, easy to store.
(3)The main advantage is the region coverer algorithm, give it a region and the maximum number of cells you want, S2 will return some cells atdifferent levels that cover the region you asked for, remember one cell corresponds to a range lookup you’ll have to perform in your database.
(4)The coverage is more accurate it means less read from the DB, less objects unmarshalling…
看到这里,你是不是很想知道,google-s2的来龙去脉,那就跟我一块解开里边神秘的面纱吧。
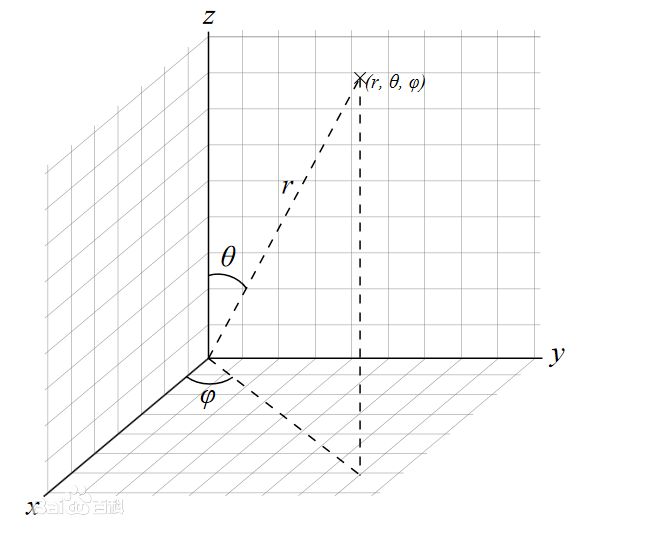
首先就是经纬度如何转换成三围空间坐标即:Point(lat, lng) ==> (x, y, z)
转化成如下:
如果看不懂,补一下数学吧。
找不到的话我就给你提供一个地方:球坐标系
其实,在我们现在讨论的问题大可不考虑 r 因为这个就是地球的半径,是个常量,不考虑就可以
那么,x, y, z就被局限在一个立方体里边了([-1, 1], [-1, 1], [-1, 1])
说到这里,我想你应该明白了吧?
如果你还不明白,请继续往下看吧
NOW : 让我们闭上眼睛,想象你的前方有一个地球,地球外表有个正立方体,刚好与地球外切。
然后,请你想想一下,你右手就是一把快刀,从中间劈下去!对,狠狠的劈下去
让我们来看一下你的成果,你的切面
不错,地球成了两半,我们只看被你伤过的切面
p呢,就是地球上的一个点,p的坐标呢我们可以表示成三围坐标系的空间坐标(x,y,z)不信,你就再看看上边吧,谁让你数学不好呢。
到这里,我们可不可以疯狂的想想一下吧,发散你的思维
假如说我们能把地球上的经纬度,能够放到外切立方体上那该多好,那么,立方体可以这样
玩过拼图吗?我们可以拼拼,最后我们拼成一个矩形
到这里,你应该自豪一下,整个世界的每个坐标都被你撕成了一个平面
不懂?
那我们回头去看那个p和那个红线,p点通过红线是不是可以映射到到正立方体的一个面上?
想象一下,整个地球的所有坐标是不是都能够按照这个方式映射到这个神奇的立方体的面上,
所以,这样我们就能把地球上的每个坐标与立方体面上的每个点做一一映射。
然而、、、、、、(是不是感觉为什么会有然而?)
我们,还是看看为什么说然而吧,我们知道
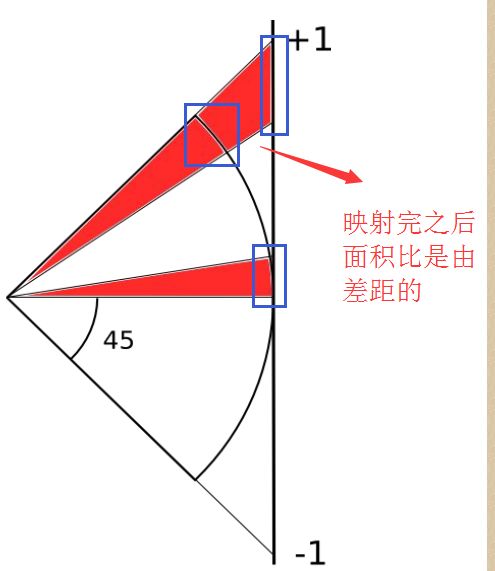
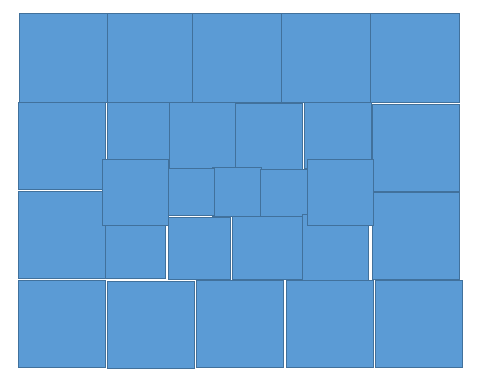
那么问题就来了,我们把地球上每个方格映射到一个立方体面上很可能就会出现如下的情况
大概是这样字,画的不好,将就着看吧。
也就是每个被映射过来的方格的面积是不均匀的。为了让他们均匀,我们要对每个地球上的坐标做一次空间变换
在google-s2中提供了三种变换形式( -1 < u < 1)
(1)线性变换,就是不做任何处理,就是跟上图差不多
(2)针对(x,y)每个值u,做
(3)针对(x,y)每个值u,做
如果u > 0
如果u < 0
到这里你会想,为什么google会选这两个函数
那就让我们看一下这两个函数在[-1,1]上的图形吧
上边是(2)下边是(3)
看曲线的走势,中间斜率大,两端斜率区域平缓,转换以后就是把边缘的方格缩小,把中间的小的方格放大,当然也不是无限放大,只是略微的调整,使得,影射在立方体面上的方格尽量的均匀化。(当然,优化的映射过程你也可以找到一个更好的,这也是一个优化的方向)
到这里,我们完成了把地球上画的方格全部映射到了外切立方体的面上了
下面就是如何给每个方格编码了
总共有六个面,不难想到,编码肯定跟面也有关系
其实在这个过程中就隐含了把点映射到希尔伯特曲线的逻辑
下面就介绍一下如何把点映射到希尔伯特曲线上
为了更好的理解这个问题,我们借鉴一下:blog.jobbole.com/81106/(版权归原创所有)
原文核心观点:曲线规定了平面上点的顺序。如果我们用这顺序来表达希尔伯特曲线,画曲线就不
值一提了。
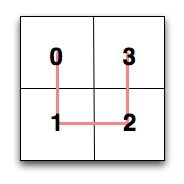
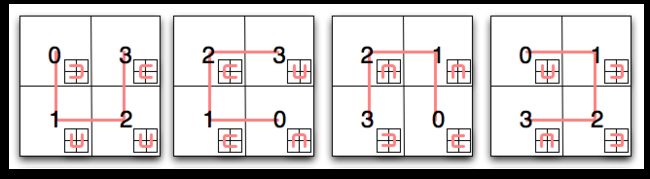
在根这一层,列举点很简单:选定一个方向和一个起始点,环绕四个象限,用0到3给他们编号。当
我们要确定访问子象限的顺序同时维护总体的邻接属性,困难就来了。通过检查我们发现,子象限
的曲线是原曲线的简单变换,而且只有四种变换。自然地,这个结论也适用于子子象限,等等。对
于一个给定的象限,我们在其中画出的曲线是由象限所在大的方形的曲线以及该象限的位置决定
的。只需要费一点力,我们就能构建出如下概况所有情况的表。
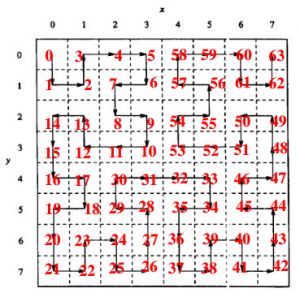
假设我们想用这个表来确定某个点在第三层希尔伯特曲线上的位置。在这个例子中,假设点的坐标
是(5,2)。(译者注:请参照下图)从上图的第一个方形开始,找到你的点所在的象限。在这个例子
中,是在右上方的象限。那么点在希尔伯特曲线上的位置的第一部分是3(二进制是11)。接着我们
进入象限3里面的方块,在这个例子中,它是(上图中的)第二个方块。重复刚才的过程:我们的点
落在哪个子象限?这次是左下角,意味着位置的下一部分是1(二进制01),我们将进入的小方块又
是第二个。最后一次重复这个过程,发现点落在右上角的子子象限,因此位置的最后部分是3(二进
制11)。把这些位置连接起来,我们得到点在曲线上的位置是二进制的110111,或者十进制的55。
就这样我们也知道了点如何映射在希尔伯俄曲线上了。
那么问题又来了,我们如何确定x,y两个边上的方格编号呢?
在google-s2源码中,是这样确认的
首先我们拿到最后映射到立方体面上的一个点(s , t)已经经过均匀化变化的
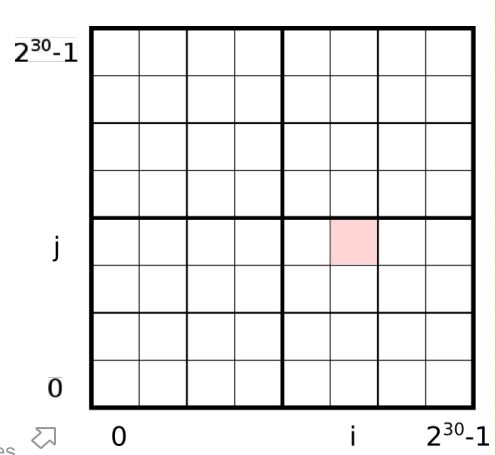
默认的,我们先进入30层的曲线填充,把平面每个纬度分成2^30 - 1个方格
现在我们就是为了找到那个(i, j)来确认方格所在位置,假设粉红色的就是p点映射的方格
p是(s, t) 其中 -1 < s , t< 1
为了找到方格的位置源码中是这样做的
Math.max(0,Math.min(2*m-1,Math.round(m*s+(m-0.5))))
其中MAX_SIZE = 2^30
其实这段代码就是为了计算(s, t)==>(i, j)即方格的位置,可以配合下图进行理解
其实m就可以理解为被黄线坐标系分割后某一个区域在横向或者纵向的纬度上的方格个数
比如说计算i 的值,首先需要s 的值,s就是在[-1, 1]上的一种坐标,现在要映射到[0, 2^30-1]上
也就是[0, 1] 被映射到 [(2^30-1)/2, 2^30-1] 即 [m-0.5, 2m-1]
为了计算p 的i 拿m*s + (2^30-1)/2也就是m*s + (m-0.5)就是i 的坐标
并其整个过程就是从地位连续空间向高维离散空间的一种离散化,这样也就是任意点到希尔伯特曲线上映射的过程
最后,就让我们一块了解一下,编码是如何做的
我们都知道,geohash的编码方式是经纬度交叉进行的,那么,s2的呢?
见证奇迹的时候到了
烧了半天脑,是不是觉得无法抵抗这种诱惑?
其实,我也是、、、
但是,革命尚未成功,我们岂能纠结于美食?
编码:
给出一个level=2的案例
编码考虑了面的属性,和希尔伯特曲线,具体的实现可以看下源码,这里不再过多赘述。
最后总结一下,只发图,不多说