广度优先搜索算法是最简便的图的搜索算法之一,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
广度优先搜索,又称宽度优先搜索。其英文全称为Breadth First Search,简称BFS。
一、基本思想
1 首先访问起始顶点v
2 接着由v出发,依次访问v的各个未访问过的邻接顶点w1,w2,…,wi;
3 然后再依次访问w1,w2,…,wi的所有未被访问过的邻接顶点;
4 依次类推,直到图中所有和v有路径相通的顶点都被访问过;
5 若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行步骤1~4,直到图中所有顶点均被访问过为止。
二、例子
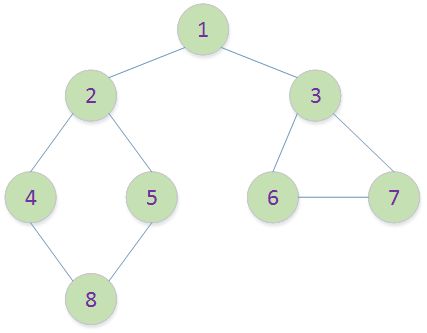
求下图的广度优先搜索顺序。
分析:可用两个队列实现,队列1里放未被搜索过的元素,队列2里放已被搜索过的元素。
步骤:
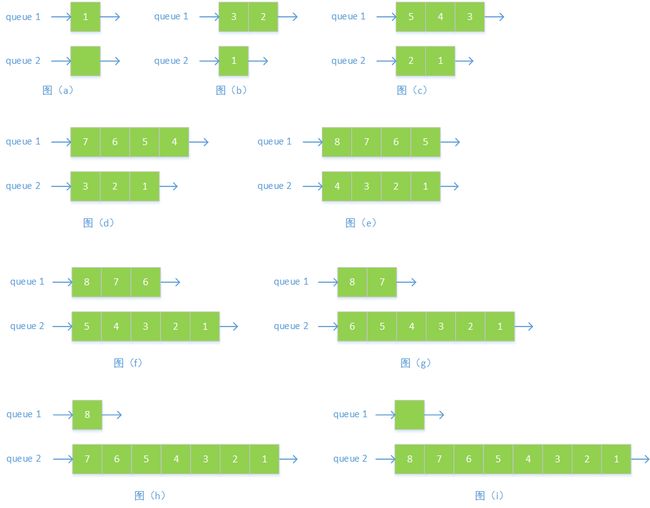
1)先把第一个元素1,放到队列1中。见图(a)
2)弹出队列1的中的队首元素,并把队首元素的相邻元素2和3,加入到队列1中;被弹出的元素则放以队列2中。见图(b)
3)重复步骤2),见图(c)~图(e)
4)若队列1的队首元素没有相邻元素,则把队列1中的元素弹出并放到队列2中,直至队列1为空,见图(f)~图(i)。整个过程结束。队列2中的元素顺序就是使用广度优先搜索方法所遍历的顺序。
三、python 3代码实现
class Graph(object):
def __init__(self,*args,**kwargs):
self.node_neighbors = {}
self.visited = {}
def add_nodes(self,nodelist):
for node in nodelist:
self.add_node(node)
def add_node(self,node):
if not node in self.nodes():
self.node_neighbors[node] = []
def add_edge(self,edge):
u,v = edge
if(v not in self.node_neighbors[u] and u != v):
self.node_neighbors[u].append(v)
self.node_neighbors[v].append(u)
def nodes(self):
return self.node_neighbors.keys()
def breadth_first_search(self, root=None):
queue = []
order = []
def bfs():
while len(queue) > 0:
node = queue.pop(0)
self.visited[node] = True
for n in self.node_neighbors[node]:
if (not n in self.visited) and (not n in queue):
queue.append(n)
order.append(n)
if root in self.nodes():
queue.append(root)
order.append(root)
bfs()
for node in self.nodes():
if not node in self.visited:
queue.append(node)
order.append(node)
bfs()
return order
if __name__ == '__main__':
g = Graph()
g.add_nodes([i+1 for i in range(8)])
g.add_edge((1, 2))
g.add_edge((1, 3))
g.add_edge((2, 4))
g.add_edge((2, 5))
g.add_edge((4, 8))
g.add_edge((5, 8))
g.add_edge((3, 6))
g.add_edge((3, 7))
g.add_edge((6, 7))
print ("Original nodes: ", g.nodes())
order = g.breadth_first_search(1)
print ("Breadth-First-Search order: ", order)
运行结果:
Original nodes: dict_keys([1, 2, 3, 4, 5, 6, 7, 8])
Breadth-First-Search order: [1, 2, 3, 4, 5, 6, 7, 8]
更多内容请关注微信公众号