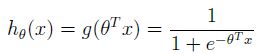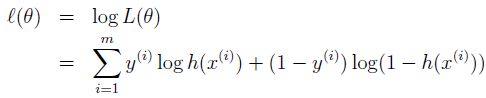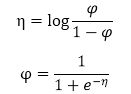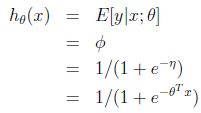目录:
1.逻辑回归
2.牛顿法求极值
3.指数分布族与多项分布
4.广义线性模型
前言
在看逻辑回归之前,先回想一下线性回归问题的求解步骤,再顺着线性回归,来介绍逻辑回归。
1.首先假设误差存在且为高斯分布,等价于真实数据的概率分布。
2.求出联合概率分布,也就是似然函数。
3.进行取对数运算,得到对数似然函数l(θ)。
4.求l(θ)的最大值,得到了最小二乘的策略。
5.使用梯度下降,让参数逐渐逼近最小二乘法中的最优解。
1.逻辑回归
逻辑回归虽然名字里带“回归”,但它不解决回归问题,而是处理分类问题。回归问题中预测值y是一系列连续值,而分类问题中y是一些离散的值。通常二分类的预测值y可以用0和1表示。例如,要建立一个垃圾邮件的分类器,那么x(i)表示邮件的特征,y是邮件的标签。当y=0时,属于正常邮件,y=1时,属于垃圾邮件。0和1分别为负例和正例,可以用符号”-“、”+“表示。现在先选择一个函数hθ(x),能够表示分类问题。我们选择下面这个函数:
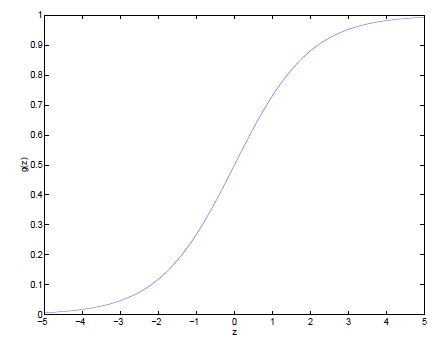
它叫做逻辑回归(logistic function,或sigmoid function),在二维坐标上是一个“S”型曲线,如图所示。
当z趋近于正无穷时,g(z)趋近于1,当z趋近于负无穷时,g(z)趋近于0。并且g(z)和h(x)的取值范围都在(0,1),相当于,把整个实数范围压缩到了0到1之间。这样,预测y的值可以表示属于某一类的概率,当y越接近1时,它属于y=1的概率越大。和线性回归一样,我们设每个特征xj的权重为θj,x0=1,所以可以求出所有权重与特征的乘积和,用向量θTx代替z,得到如下表达式:
确定了处理二分类问题的模型,接下来就是求解θ了。像最小二乘的推导一样,我们对分类模型也做一些假设,用最大似然法和来优化θ。假设给定x和θ,输出值hθ(x)表示y=1的概率,那么y=0的概率就是1- hθ(x)。
可以将两个式子合并:
假设所有样本都是独立分布,接着求出参数的似然性:
为方便后面的计算,对它取对数,将累乘变成累和:
我们的目标就是找到θ,使对数似然性最大。为了求它的最大值,可以使用梯度下降的思想,逐步迭代,最终求极大值。所以这里可以叫做梯度上升法。那么接着对这个函数求偏导:
顺便提一下logistic函数求导,根据链式求导法则得到如下表达式:
现在就得到了梯度上升的迭代公式:
准确来说,得到的是随机梯度上升的公式,即每进行一个样本的拟合,就更新一次参数。与之相对应的,是批梯度上升。
虽然决策函数hθ(x(i))是一个非线性的函数,这个公式是由一个不同的算法推导出来,但是推导过程与最终结果都与线性回归与最小二乘法差不多,接下来就介绍另一种求极值的方法。
2.牛顿法
梯度下降法和牛顿法都是为了求函数最优解,但是方式不同。梯度下降法的步骤是,选择一组随机值,计算函数的导数,接着沿着导数的反方向,也就是沿着下降的方向前进一步,逐步逼近最小值。而当一个函数存在极值时,它的极值点处的一阶导数等于0,那么用迭代的方法逐步逼近一阶导数为0的位置,就是牛顿法的核心思想。接下来看具体步骤:
上图是某函数的一阶导数f(x),要求y=0位置处的值,首先随机取一点A,做A的切线,交x轴于θ(1),再过做x轴垂线,交f(x)于点B,再做B的切线,以此类推,逼近极值点。那么根据导数和线段上的关系,有以下表达式:
其中f(x)是逻辑回归里的似然函数l(θ)的导数,于是牛顿法求似然函数的迭代公式为:
当参数θ是一个向量时,牛顿法表示如下,∇θ l(θ)是对l(θ)求θ的偏导数,H表示Hessian矩阵:
牛顿法通常比梯度下降法的收敛速度更快,对逻辑回归的效果很好,经过较少的迭代次数就能得到较高的精度,但它也有缺点。牛顿法适用条件比较复杂,不像如梯度下降适用性那么广。而且牛顿法需要计算Hessian矩阵,当参数较多时,运算量会很大:
3.指数分布族与多项分布
其他函数也能作为分类函数,理论上只要在0到1之间且单调即可。不过逻辑斯蒂函数与伯努利分布不是随便写出来的,它和线性回归一样,都是指数分布族的一个特例。指数族分布可以写成如下形式:
η是分布的自然参数;
T(y)为充分统计量;
a(η)为对数分配函数。
当给定一组a,b,T,这个公式就定义了一个概率分布的集合。
对于伯努利二项分布,假设它的参数是φ,类别用0,1表示,可以这么表达:
p(y = 1; φ) = φ
p(y = 0; φ) = 1 – φ
那么伯努利分布可以改写成如下形式:
所以参数
这就得到了sigmoid函数。所以总结一下,当指数分布族满足以下条件时,可以推出伯努利分布。
除了高斯分布、伯努利分布,多项式分布也属于指数分布族。多项式分布可以解决多分类问题,可以认为是二项分布的延伸。这里直接给出多分类问题的模型函数,具体推导这篇文章里写的很详细。
4.广义线性模型
当我们要对单位时间内随机事件发生的个数进行建模,我们可以用泊松分布;对二项分布问题建模,可以使用伯努利分布建模;但是,如果遇到一个特定的问题,没有现成的模型可以使用时,我们就需要广义线性模型来建立一套算法。为了推导出这些问题的模型,要对y的分布做以下三个假设:
1.给定x与θ,输出y属于指数族分布,并以η为参数。
2.模型的目标是预测T(y)的期望值,即h(x) = E[T(y)|x]。
3.η和输入x是线性关系:η= θTx。
还是以二项分布为例,用广义线性模型来对它建模。给定x,θ后,二项分布的输出值应该是属于某一类的概率,h(x) = E[y|x],期望值就是y=1的概率,P(y=1|x;θ)=φ,根据上文的已经推出的结论φ=1/(1+e^(-η) ),且η= θTx,于是得到:
本文主要参考:
吴恩达课程
拾毅者博客
玉心sober博客