2016 summer &

index picture

1、递归与分治法

递归的基本思想：一个直接或间接调用自身的算法

（1）斐波那契数列:

斐波那契数列递归以及递归优化

分治法的基本思想：将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且与原问题相同。递归地解决这些子问题，然后将各子问题的解合并得到原问题的解。

（1）排列问题：

先贴出可能用到的代码：

交换两个数的模板：

交换函数

问题：已知R={1,2,3},对它产生全排列

分析：当第一个数1固定，对23进行全排列，可以分为当2固定，对3进行全排列；当3固定，对2进行全排，则可以得到123,132;其余当第一个数是2，对13进行全排列；当第一个数是3，对12进行全排列。

程序代码：

全排列

（2）整数划分问题

问题：

整数划分问题

程序代码：

整数划分

（3）二分搜索技术：

问题：给定已排好序的n个元素a[0,n-1],现要在这n个元素中找出一特定元素x

程序代码：

循环实现：

二分搜索循环

递归实现：

二分搜索递归

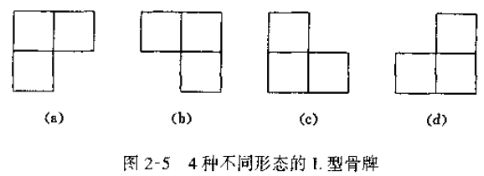
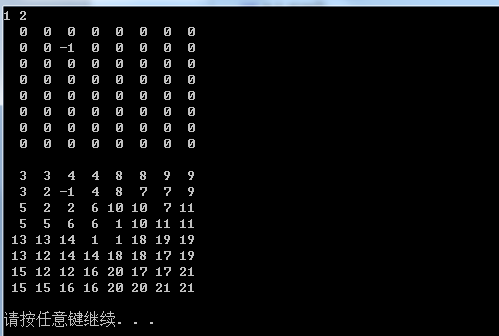
（4）棋盘覆盖

先贴出可能用到的代码：

动态申请一个一维数组：

动态申请一维数组

动态开辟一个二维数组：

动态开辟一个二维数组

问题：

问题

l型骨牌

分析：可以用分治法解决此问题，当k > 0时，将2^k * 2^k的棋盘分割为4个2^(k-1) * 2^(k-1)个子棋盘，如下图：

分割与填法

上图中的右图就是我们填L型骨牌的方式，使得每一个区域都有一个特殊方格。

代码一

代码二

运行结果

（5）合并排序

基本思想：当n=1时，终止排序；否则将待排序的元素分割为大小大致相同的两个子集和，分别对子集和进行排序，最终将排好序的子集和合并。

代码一

代码二

（6）快速排序

快速排序

注：若数据是基本有序的，则快速排序的效率不高，可以用随机化法解决：

随机化法

（7）线性时间选择

问题：给定线性序集中n个元素和一个整数k，要求找出这n个元素中第k小的元素。

分析：利用分治法，调用Partition函数可以对其进行划分，一次划分得到第pos个小的元素，然后判断k值与pos的大小，分别对部分重复上述步骤，最主要的是pos的求法是index-left+1

找第k小的元素

2、动态规划算法

基本思想：将待求解的问题分解为若干个子问题，先求解子问题，然后从这些子问题得到原问题的解。经动态规划法得到的子问题往往不是相互独立的，为了避免重复计算，我们可以用一个表来记录所有已解决的子问题的答案。它常用于求解具有最优子结构性质（问题的最优解包含了子问题的最优解）和子问题重叠性质（在用递归算法自顶向下的解决问题时，每次产生的子问题并不总是新问题，有些问题被反复计算多次）的问题。

基本步骤：a、找出最优解的性质，并刻画其特征；

b、递归地定义最优值；

c、以自底向上的方式计算出最优值；

d、根据计算最优值时得到的信息，构造一个最优解。

（1）矩阵连乘问题

两个矩阵相乘代码：

矩阵相乘

问题：给定n个矩阵{A1，A2，A3.........An}，计算出n个矩阵连乘积的最优计算次序

分析：

a、最优解的性质：设A[1,n]是n个矩阵的连乘，则可将其划分为A[1,k]和A[k+1,n]

b、递归地定义最优值：设m[i,j]为所需的最少数乘次数，则当i=j时，m[i,j]=0；当i

m[i,j] = min(m[i,k]+m[k+1,j]+p[i-1]*p[k]*p[j]),其中k取值范围是i到j-1；

c、以自底向上计算最优值

d、构造一个最优解

（2）最长公共子序列

规定：子序列是按照下标递增的方式

问题：给定两个序列分别是：X={A,B,C,B,D,A,B},Y={B,D,C,A,B,A},假设Z是X和Y的最长公共子序列，求Z？

分析：

a、最优解的性质：若xm = yn，则zk = xm = yn，z(k-1)是x(m-1)和y(n-1)的最长公共子序列；若xm!=yn且zk!=xm，则z是x(m-1)和yn的最长公共子序列；若xm!=yn且zk!=yn，则z是xm和y(n-1)的最长公共子序列；

b、递归地定义最优值：用c[i][j]记录xi和yj最长公共子序列的长度。当i=j=0时，c[i][j]=0;当i,j>0时，若xi=yj,则c[i][j]=c[i-1][j-1]+1;若xi!=yj,则c[i][j] =max(c[i][j-1],c[i-1][j])。

c、以自底向上计算最优值

d、构造一个最优解

（3）0-1背包问题

问题：

0-1背包问题

分析：

a、最优解的性质：假设对于n元0-1向量x={x1,x2……xn}，有Sum(wi xi) <= c && Max(Sum(vi xi))为最优解，则有对于x={x2……xn}，有Sum(wi xi) - w1 x1 <= c && Max(Sum(vi xi)-v1 x1)为最优解

b、递归地定义最优值：设m(i,j)代表最大价值，i表示为i……n,即放入了这么些物品，j代表当前容器的容量。则有第一种情况当i==n，如果j>w[n]，则返回v[n],否则返回0；第二种情况当i < n时，若jw[i],则返回Max( m(i+1,j) , (m(i+1,j-w[i]) + v[i] ) )

c、以自底向上计算最优值：