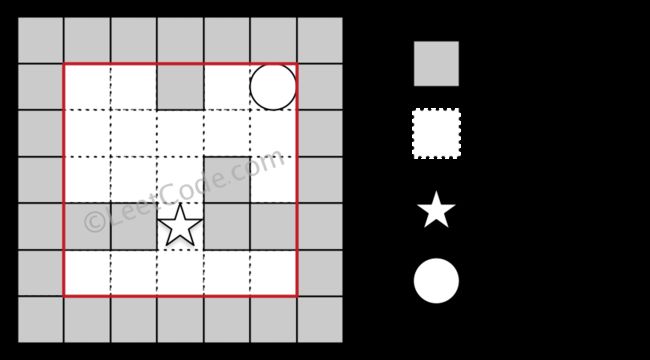
Descriptio
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the ball's start position, the destination and the maze, determine whether the ball could stop at the destination.
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.
Example 1
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
Example 2
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)
Output: false
Explanation: There is no way for the ball to stop at the destination.
Note:
- There is only one ball and one destination in the maze.
- Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
- The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.
Solution
DFS
一眼就知道要用DFS或者BFS去做的题,但是如何避免重复路径呢?将所有路径上的点做标记,然后不允许重复?这样是不行的,因为有的路径里面就是有交叉的。记录下来前一层递归的方向,然后不能反方向走?这样逻辑就太复杂了,不好写。
正确的做法是,标记start[],不能重复以同一个坐标作为起点!至于路径中滑过的那些位置不必计较,只需要在球能停住的位置做标记就行了。
还需要注意的是,不需要回溯!因为对于每个start来说,从它出发达不到终点就是达不到,无论开始从哪条路径到达该start,然后继续往下走都会失败的。所以不需要回溯。
class Solution {
public static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
return dfs(maze, start, destination, new HashSet<>());
}
private boolean dfs(int[][] maze, int[] start, int[] dest, Set visited) {
if (start[0] == dest[0] && start[1] == dest[1]) { // meet destination
return true;
}
int index = start[0] * maze[0].length + start[1]; // convert 2D to 1D
if (!visited.add(index)) { // decides if start[] has already been set as start and failed
return false;
}
for (int[] d : DIRECTIONS) { // try each direction
int x = start[0];
int y = start[1];
while (isEmpty(maze, x + d[0], y + d[1])) {
x += d[0];
y += d[1];
}
if (dfs(maze, new int[] {x, y}, dest, visited)) {
return true;
}
}
// important: no need to backtrack!!!
return false;
}
public boolean isEmpty(int[][] maze, int i, int j) {
return isValid(maze, i, j) && maze[i][j] != 1;
}
public boolean isValid(int[][] maze, int i, int j) {
return i >= 0 && i < maze.length && j >= 0 && j < maze[0].length;
}
}
由于数组中只有0或1,可以用flag标记visited,省略掉额外的HashSet:
class Solution {
public static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
return dfs(maze, start, destination);
}
private boolean dfs(int[][] maze, int[] start, int[] dest) {
if (start[0] == dest[0] && start[1] == dest[1]) { // meet destination
return true;
}
if (maze[start[0]][start[1]] == -1) { // decide if already visited as start and failed
return false;
}
maze[start[0]][start[1]] = -1; // mark visited as start
for (int[] d : DIRECTIONS) { // try each direction
int x = start[0];
int y = start[1];
while (isEmpty(maze, x + d[0], y + d[1])) {
x += d[0];
y += d[1];
}
if (dfs(maze, new int[] {x, y}, dest)) {
return true;
}
}
// important: no need to backtrack!!!
return false;
}
public boolean isEmpty(int[][] maze, int i, int j) {
return isValid(maze, i, j) && maze[i][j] != 1;
}
public boolean isValid(int[][] maze, int i, int j) {
return i >= 0 && i < maze.length && j >= 0 && j < maze[0].length;
}
}
BFS
根据DFS的思路,可以轻松改成BFS。
class Solution {
public static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
int m = maze.length;
int n = maze[0].length;
Queue queue = new LinkedList<>();
boolean[][] visited = new boolean[m][n];
queue.offer(start);
visited[start[0]][start[1]] = true;
while (!queue.isEmpty()) {
int[] pos = queue.poll();
if (pos[0] == destination[0] && pos[1] == destination[1]) {
return true;
}
for (int[] direction : DIRECTIONS) {
int x = pos[0];
int y = pos[1];
while (isEmpty(maze, x + direction[0], y + direction[1])) {
x += direction[0];
y += direction[1];
}
if (!visited[x][y]) {
queue.offer(new int[] {x, y});
visited[x][y] = true;
}
}
}
return false;
}
public boolean isEmpty(int[][] maze, int i, int j) {
return isValid(maze, i, j) && maze[i][j] != 1;
}
public boolean isValid(int[][] maze, int i, int j) {
return i >= 0 && i < maze.length && j >= 0 && j < maze[0].length;
}
}
可以省略掉visited[][],直接在maze上加flag:
class Solution {
public static final int[][] DIRECTIONS = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
int m = maze.length;
int n = maze[0].length;
Queue queue = new LinkedList<>();
queue.offer(start);
maze[start[0]][start[1]] = -1;
while (!queue.isEmpty()) {
int[] curr = queue.poll();
if (isEqual(curr, destination)) {
return true;
}
for (int[] d : DIRECTIONS) {
int x = curr[0];
int y = curr[1];
while (canMoveTo(maze, x + d[0], y + d[1])) {
x += d[0];
y += d[1];
}
if (maze[x][y] != 0) {
continue;
}
queue.offer(new int[] {x, y});
maze[x][y] = -1;
}
}
return false;
}
private boolean isEqual(int[] a, int[] b) {
for (int i = 0; i < a.length; ++i) {
if (a[i] != b[i]) {
return false;
}
}
return true;
}
private boolean canMoveTo(int[][] maze, int i, int j) {
return i >= 0 && i < maze.length && j >= 0 && j < maze[0].length
&& maze[i][j] != 1;
}
}