本文是对论文《The Z1: Architecture and Algorithms of Konrad Zuse’s First Computer》的中文翻译,已征得原作者Raul Rojas的同意。感谢Rojas教授的支持与帮助,感谢在美留学的好友——锁在英语方面的指导。本人英文和专业水平有限,不妥之处还请批评指正。
This is a translation of "The Z1: Architecture and Algorithms of Konrad Zuse's First Computer" with the permission of its author Raul Rojas. Many thanks for the kind support and help from Prof. Rojas. And thanks to my friend Suo, who's currently in the US, for helping me with my English. The translation is completed to the best of my knowledge and ability. Any comments or suggestions would be greatly appreciated.
摘要
本文首次给出了对Z1的综合介绍,它是由德国发明家康拉德·祖思(Konrad Zuse)1936~1938年期间在柏林建造的机械式计算机。文中对该计算机的主要结构零件、高层架构,及其组件之间的数据交互进行了描述。Z1能用浮点数进行四则运算。从穿孔带读入指令。一段程序由一系列算术运算、内存读写、输入输出的指令构成。使用机械式内存存储数据。其指令集没有实现条件分支。
虽然,Z1的架构与祖思在1941年实现的继电器计算机Z3十分相似,它们之间仍然存在着明显的差异。Z1和Z3都通过一系列的微指令实现各类操作,但前者用的不是旋转式开关。Z1用的是数字增量器(digital incrementer)和一套状态位,它们可以转换成作用于指数和尾数单元以及内存块的微指令。计算机里的二进制零件有着立体的机械结构,微指令每次要在12个层片(layer)中指定一个使用。在浮点数规格化方面,没有考虑尾数为零的异常处理,直到Z3才弥补了这一点。
文中的知识源自对祖思为Z1复制品(位于柏林德国技术博物馆)所画的设计图、一些信件、笔记本中草图的仔细研究。尽管这台计算机从1989年展出至今(停运状态),始终没有关于其体系结构详细的、高层面的阐述可寻。本文填补了这一空白。
1 康拉德·祖思与Z1
德国发明家康拉德·祖思在1936~1938年期间建造了他的第一台计算机注1(1934~1935年期间做过一些小型机械线路的实验)。在德国,祖思被视为计算机之父,尽管他在第二次世界大战期间建造的计算机在毁于火灾之后才为人所知。祖思的专业是夏洛腾堡工学院(Technische Hochschule Charlottenburg)(现今的柏林工业大学)的土木工程。他的第一份工作在亨舍尔公司(Henschel Flugzeugwerke),这家公司恰巧从1933年开始建造军用飞机[1]。这位25岁的小年轻,负责完成生产飞机部件所需的一大串结构计算。而他在学生时代,就早已开始考虑机械化计算的可能性[2]。所以他在亨舍尔才干了几个月就辞职,建造机械计算机去了,还开了自己的公司,事实也正是世界上第一家计算机公司。
注1:康拉德·祖思建造计算机的精确年表,来自于他从1946年3月起手记的小本子。本子里记载着,V1建造于1936~1938年间。
在1936~1945年期间,祖思根本停不下来,哪怕被两次短期地召去前线。每一次都最终被召回柏林,继续从事在亨舍尔和自己公司的工作。在这九年间,他建造了如今我们所知的6台计算机,分别是Z1、Z2、Z3、Z4,以及专业领域的S1和S2。后四台建造于第二次世界大战开始之后。Z4是在世界大战结束前的几个月里建好的。祖思一开始给它们的简称是V1、V2、V3、V4(取自实验模型或者说原型(Versuchsmodell)的首字母)。战争结束之后,他把V改成了Z,原因很明显译者注。V1(也就是后来的Z1)是项迷人的黑科技:它是台全机械的计算机,却没有用齿轮表示十进制(前个世纪的巴贝奇这么干,正在做霍尔瑞斯制表机的IBM也这么干),祖思要建的是一台全二进制计算机。机器基于的部件里用小杆或金属板的直线移动表示1,不移动表示0(或者相反,因部件而异)。祖思开发了新型的机械逻辑门,并在他父母家的客厅里做出第一台原型。他在自传里提到了发明Z1及后续计算机背后的故事[2]。
译者注:祖思把V改成Z,是为了避免与韦纳·冯·布劳恩(Wernher von Braun)研制的火箭的型号名相混淆。
Z1身为机械,却竟也是台现代计算机:基于二进制,使用浮点型表示数据,并能进行四则运算。从穿孔带读入程序(虽然没有条件分支),计算结果可以写入(16字大小的)内存,也可以从内存读出。机器周期在4Hz左右。
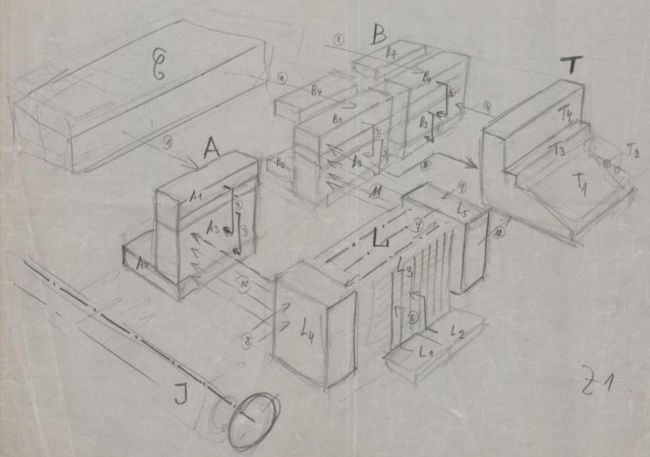
Z1与1941年建成的Z3十分相像,Z3的体系结构在《Annals of the History of Computing》中已有描述[3]。然而,迄今仍没有对Z1高层架构细节上的阐述。最初那台原型机毁于1943年的一场空袭。只幸存了一些机械部件的草图和照片。20世纪80年代,康拉德·祖思在退休多年之后,在西门子和其他一些德国赞助商的赞助之下,建造了一台完整的Z1复制品,今藏于柏林的技术博物馆(如图1所示)。有两名做工程的学生帮着他完成:那几年间,在德国欣费尔德的自家里,他备好全套图纸,精心绘制每一个(要从钢板上切割出来的)机械部件,并亲自监工。Z1复制品的第一套图纸绘制于1984年。1986年4月,祖思画了张时间表,预期能在1987年12月完成机器的建造。1989年,机器移交给柏林博物馆的时候,做了不少次运行和算术运算的演示。然而,Z1复制品和之前的原型机一样,从来都不够可靠,无法在无人值守的情况下长时间运行。甚至在揭幕仪式上就挂了,祖思花了几个月才修好。1995年祖思去世之后,这台机器就再没有启动过。
尽管我们有了柏林的Z1复制品,命运却第二次同我们开了玩笑。除了绘制Z1复制品的图纸,祖思并没有正儿八经地把有关它从头至尾的详尽描述写出来(他本意想交给当地的大学来写)。这事儿本是相当必要的,因为拿复制品和1938年的Z1照片对比,前者明显地「现代化」了。80年代高精密的机械仪器使祖思得以在建造机器时,把钢板制成的层片排布得更加紧密。新Z1很明显比它的前身要小得多。而且有没有在逻辑和机械上与前身一一对应也不好说,祖思有可能吸收了Z3及其他后续机器的经验,对复制品做了改进。在1984~1989年间所画的那套机械图纸中,光加法单元就出现了至少6种不同的设计方案,散布于5~8个、最终乃至12个机械层片之间注2。祖思没有留下详细的书面记录,我们也就莫名其妙。更糟糕的是,祖思既然第二次建造了Z1,却还是没有留下关于它综合性的逻辑描述。他就像那些著名的钟表匠,只画出表的部件,不做过多阐释——一流的钟表匠确实也不需要过多的说明。他那两个学生只帮忙写了内存和穿孔带读取器的文档,已经是老天有眼[4]。柏林博物馆的参观者只能看着机器里头成千上万的部件惊叹。惊叹之余就是绝望,即使专业的计算机科学家,也难以设想这头机械怪物内部的工作机理。机器就在这儿,但很不幸,只是尸体。
注2:你可以在我们的网页「Konrad Zuse Internet Archive」上找到Z1复制品的所有图纸。
为写这篇论文,我们仔细研究了Z1的图纸和祖思记事本里零散的笔记,并在现场对机器做了大量的观察。这么多年来,Z1复制品都没有运行,因为里头的钢板被压弯了。我们查阅了超过1100张机器部件的放大图纸,以及15000页的笔记本内容(尽管里头只有一小点有关Z1的信息)。我只能看到一段计算机一部分运作的短视频(于几近20年前录制)。慕尼黑的德意志博物馆收藏了祖思论文里出现的1079张图纸,柏林的技术博物馆则收藏了314张。幸运的是,一些图纸里包含着Z1中部分微指令的定义和时序,以及一些祖思一位一位手写出来的例子。这些例子可能是祖思用以检验机器内部运算、发现bug的。这些信息犹如罗塞塔石碑,有了它们,我们得以将Z1的微指令和图纸联系起来,和我们充分理解的继电器计算机Z3(有全套线路信息[5])联系起来。Z3基于与Z1一样的高层架构,但仍存在一些重要差异。
本文由浅入深:首先,了解一下Z1的分块结构、机械部件的布局,以及祖思用到的一些机械门的例子。而后,进一步深入Z1的核心零件:时钟控制的指数和尾数加法单元、内存、算术运算的微序列器。介绍了机械零件之间如何相互作用,「三明治」式的钢板布局如何组织计算。研究了乘除法和输入输出的过程。最后简要总结了Z1的历史地位。
2 分块结构
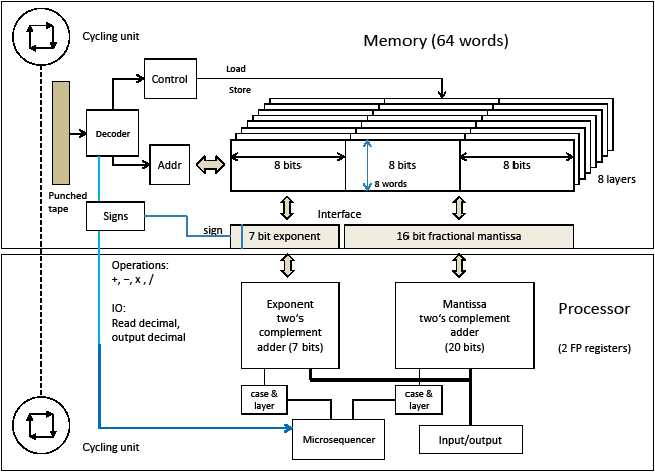
Z1是一台时钟控制的机器。作为机械设备,其时钟被细分为4个子周期,以机械部件在4个相互垂直的方向上的移动来表示,如图3所示(左侧「Cycling unit」)。祖思将一次移动称为一次「衔接(engagement)」。他计划实现4Hz的时钟周期,但柏林的复制品始终连1Hz(4衔接/秒)都超不过。以这速度,一次乘法运算要耗时20秒左右。
Z1的诸多特性被后来的Z3所采用。以现在的眼光来看,Z1(见图3)中最重要的革新如有:
基于完全的二进制架构实现内存和处理器。
内存与处理器分离。在复制品中,机器大约一半由内存和穿孔带读取器构成。另一半由处理器、I/O控制台和微控制单元构成。原Z1的内存容量是16字,复制品是64字。
可编程:从穿孔带读入8比特长的指令(其中2位表示操作码译者注、6位表示内存地址,或者以3位表示四则运算和I/O操作的操作码)。因此指令只有8种:四则运算、内存读写、从十进制面板读入数据、将结果寄存器里的内容显示到十进制展板。
译者注:应是指内存读写的操作码。
内存和处理器中的内部数据以浮点型表示。于是,处理器分为两个部分:一部分处理指数,另一部分处理尾数。位于二进制小数点后面的尾数占16个比特。(规格化的浮点数)小数点左边那位永远是1,不需要存。指数占7位,以2的补数形式表示(-64~+63)。用额外的1个比特来存储浮点数的符号位。所以,存储器中的字长为24位(16位尾数、7位指数、1位符号位)。
参数或结果为0的特殊情况(规格化的尾数无法表示,它的第一位永远是1)由浮点型中特殊的指数值来处理。这一点到了Z3才实现,Z1及其复制品都没有实现。因此,Z1及其复制品都处理不了中间结果有0的情况。祖思知道这一短板,但他留到更易接线的继电器计算机上去解决。
CPU是微代码结构的:操作被分解成一系列微指令,一个机器周期一条微指令。微指令在算术逻辑单元(ALU)之间产生具体的数据流,ALU不停地运作,每个周期都将两个输入寄存器里的数加一遍。
神奇的是,内存和处理器可以分别独立运行:只要穿孔带给出命令,内存就在通信接口写入或读取数据。处理器也将在执行存取操作时在通信接口写入或读取。可以关闭内存而只运行处理器,此时原本来自内存的数据将变为0。也可以关了处理器而只运行内存。祖思因而可以单独调试机器的两个部分。同时运作时,有一根连接两者周期单元的轴将它们同步起来。
Z1的其他革新与后来Z3中体现出来的想法相似。Z1的指令集与Z3几乎一样,但它算不了平方根。Z1利用废弃的35毫米电影胶卷作为穿孔带。
图3展示了Z1复制品的抽象图。注意机器的两个主要部分:上半部分是内存,下半部分是处理器。每部分都有其自己的周期单元,每个周期进一步分为4个方向上(由箭头标识)的机械移动。这些移动可以靠分布在计算部件下的杠杆带动机器的任何部分。一次读入一条穿孔带上的指令。指令的持续时间各不相同。存取操作耗时一个周期,其他操作则需要多个周期。内存地址位于8位操作码的低6位比特中,允许程序员寻址64个地址。
如图3所示译者注,内存和处理器通过彼此各单元之间的缓存进行通信。在CPU中,尾数的内部表示扩到了20位:二进制小数点前加两位(以表示二进制幂21和20),还有两位表示最低的二进制幂(2-17和2-18),旨在提高CPU中间结果的精度。处理器中20位的尾数可以表示21~2-18的二进制幂。
译者注:原文写的是「图1」,我觉得是作者笔误,应为「图3」。
解码器从穿孔带读取器获得指令,判断好操作之后开始按需控制内存单元和处理器。(根据加载指令)将数从内存读到CPU两个浮点数寄存器之一。再根据另一条加载指令将数从内存读到另一个CPU寄存器中。这两个寄存器在处理器里可以相加、相减、相乘或相除。这类操作既涉及尾数的相加,也涉及指数的加减(用2的补码加法器)。乘除结果的符号位由与解码器直接相连的「符号单元」处理。
穿孔带上的输入指令会使机器停止,以便操作人员通过拨动机械面板上的4个十进制位输入数据,同时通过一根小杆输入指数和符号。而后操作员可以重启机器。输出指令也会使机器停止,将结果寄存器中的内容显示到十进制机械面板上,待操作员按下某根小杆,机器重新运行。
图3中的微序列器和指数尾数加法单元共同组成了Z1计算能力的核心。每项算术或I/O操作都被细分为多个「阶段(phases)」。而后微序列器开始计数,并在加法单元的12层机械部件中选择相应层片上合适的微操作。
所以举例来说,穿孔带上最小的程序可以是这样的:1) 从地址1(即第1个CPU寄存器)加载数字;2) 从地址2(即第2个CPU寄存器)加载数字;3) 相加;4) 以十进制显示结果。这个程序因而允许操作员预先定义好一坨运算,把Z1当做简单的机械计算器来用。当然,这一系列运算可能长得多:可以把内存当做存放常量和中间结果的仓库,编写自动化的系列运算(在后来的Z4计算机中,做数学计算的穿孔带能有两米长)。
Z1的体系结构可以用如下的现代术语来总结:这是一台可编程的通用浮点型冯·诺依曼机(处理器和内存分离),有着只读的外部程序,和24位、16字的存储空间。可以接收4位数的十进制数(以及指数和符号)作为输入,然后将转换为二进制。可以对数据进行四则运算。二进制浮点型结果可以转换回科学记数法表示的十进制数,方便用户读取。指令中不包含条件或无条件分支。也没有对结果为0的异常处理。每条指令拆解为机器里「硬接线」的微指令。微序列器规划着微指令的执行。在一个仅存的机器运行的视频中,它宛若一台织布机。但它编织的是数字。
3 机械部件的布局
柏林的Z1复制品布局非常清晰。所有机械部件似乎都以完美的方式布放。我们先前提过,对于处理器,祖思至少设计了6个版本。但是主要部件的相对位置一开始就确定了,大致能反映原Z1的机械布局。主要有两个部分:分别是的内存和处理器,由缝隙隔开(如图3所示)。事实上,它们分别安装在带滚轮的桌子上,可以扯开了进行调试。在水平方向上,可以进一步把机器细分为包含计算部件的上半部分和包含所有同步杠杆的下半部分。参观者只有弯腰往计算部件下头看才能看到Z1的「地下世界」。图4是设计图里的一张绘稿,展示了处理器中部分计算和同步的层片。请看那12层计算部件和下侧区域的3层杠杆。要理解那些绘稿是有多难,这张图纸就是个绝好的例子。上面尽管有不少关于各部件尺寸的细节,但几乎没有其功用方面的注解。
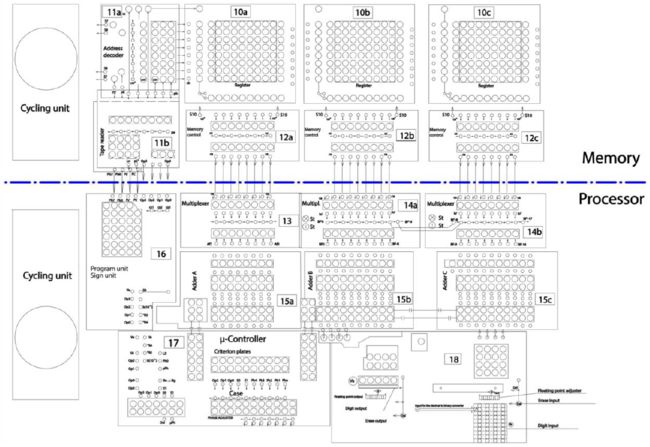
图5是祖思画的Z1复制品俯视图,展示了逻辑部件的分布,并标注了每个区域的逻辑功能(这幅草图在20世纪90年代公开)。在上半部分,我们可以看到3个存储仓。每个仓在一个层片上可以存储8个8比特长的字。一个仓有8个机械层片,所以总共能存64字。第一个存储仓(10a)用来存指数和符号,后两个(10b、10c)存低16位的尾数。用这样的比特分布存放指数和尾数,只需构建3个完全一样的8位存储仓,简化了机械结构。
内存和处理器之间设有「缓存」(12abc),用于与处理器进行数据交互。不能在穿孔带上直接设常数。所有的数据,要么由用户从十进制输入面板(图右侧18)输入,要么是计算机自己算得的中间结果。
图中的所有单元都仅仅展示了最顶上的一层。切记Z1可是建得犹如一坨机械「三明治」。每一个计算层片都与其上下层片严格分离(每一层都有金属的地板和天花板)。层间的通信靠垂直的小杆实现,它们可以把移动传递到上层或下层去。画在表示计算层片的矩形之间的小圆圈就是这些小杆。矩形里那些稍大一点的圆圈代表逻辑操作。我们可以在每个圆圈里找见一个二进制门(纵贯层片,每个圆圈最多有12个门)。根据此图,我们可以估算出Z1中逻辑门的数量。不是所有单元都一样高,也不是所有层片都布满着机械部件。保守估计,共有6000个二进制零件组成的门。
祖思在图5中给机器的不同模块标上号。各模块的作用如下:
内存区域
- 11a:6位内存地址的解码器
- 11b:穿孔带读取器和操作码解码器
- 10a:7位指数和符号的存储仓
- 10b、10b:尾数小数部分的存储仓
- 12abc:加载或存储操作下与处理器交互的接口
处理器区域
- 16:控制和符号单元
- 13:指数部分中两个ALU寄存器的多路复用器
- 14ab:ALU寄存器的多路复用器,乘除法的1比特双向移位器
- 15a:指数的ALU
- 15bc:规格化尾数的20位ALU(18位用于小数部分)
- 17:微代码控制
- 18:右侧是十进制输入面板,左侧是输出面板
不难想象这幅示意图中从上至下的计算流程:数据从内存出来,进入两个可寻址的寄存器(我们称为F和G)。这两个寄存器是沿着区域13和14ab分布的。再把它们传给ALU(15abc)。结果回传给寄存器F或G(作为结果寄存器),或回传到内存。可以使用「反译」(从二进制转换为十进制)指令将结果显示为十进制。
下面我们来看看各个模块更多的细节,集中讨论主要的计算部件。
4 机械门
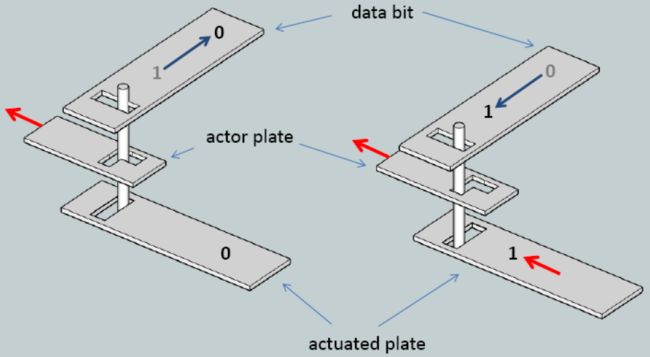
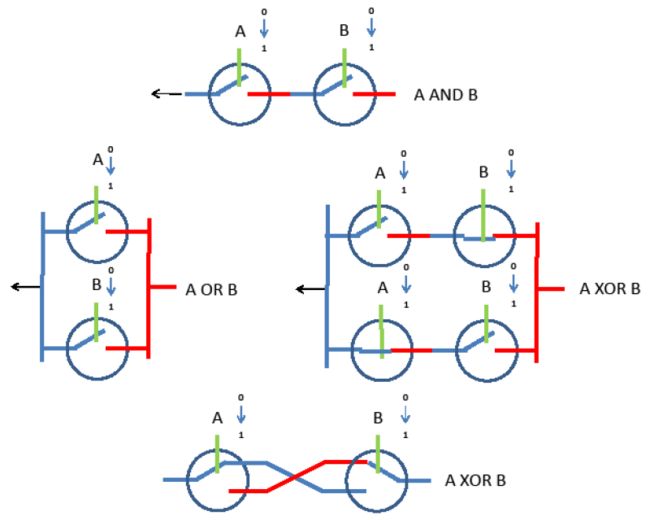
理解Z1机械结构的最好办法,莫过于搞懂那几个祖思所用的二进制逻辑门的简单例子。表示十进制数的经典方式一向是旋钮表盘。把一个齿轮分为10个扇区——旋转齿轮可以从0数到9。而祖思早在1934年就决定使用二进制系统(他跟着莱布尼兹称之为「the dyadic system」)。在祖思的技术中,一块平板有两个位置(0或1)。可以通过线性移动从一个状态转移到另一个状态。逻辑门根据所要表示的比特值,将移动从一块板传递到另一块板。这一结构是立体的:由堆叠的平板组成,板间的移动通过垂直放置在平板直角处的圆柱形小杆或者说销钉实现。
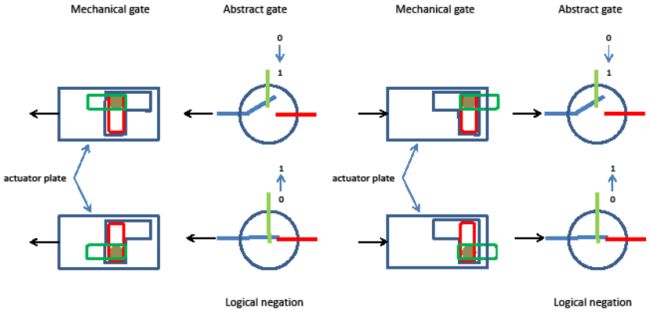
我们来看看三种基本门的例子:合取、析取、否定。其主要思想可以有多种机械实现,而有创意如祖思总能画出适应机器立体结构的最佳方案。图6译者注展示了祖思口中的「基本门(elementary gate)」。「使动板(actor plate)」可以视作机器周期。这块板循环地从右向左再向后移动。上面一块板含着一个数据位,起着控制作用。它有1和0两个位置。贯穿板洞的小杆随着平板水平移动(自身保持垂直)。如果上面的板处于0位置,使动板的移动就无法传递给受动板(actuated plate)(见图6左)。如果数据位处于1位置,使动板的移动就可以传递给受动板。这就是康拉德·祖思所谓的「机械继电器」,就是一个可以闭合机械「电流」的开关。该基本门以此将数据位拷贝到受动板,这个数据位的移动方向转了90度。
译者注:原文「Fig. 5」应为笔误。
图7展示了这种平板布局的俯视图。可以看到使动板上的洞口。绿色的控制板可以将圆圈(小杆)拉上拉下。当小杆处于能被使动板扯动的位置时,受动板(红色)才可以左右移动。每一张机械俯视图右侧都画有等效的逻辑开关。数据位能开闭逻辑门,推拉使动板(如箭头所示)。祖思总是习惯把开关画在0位置,如图7所示。他习惯让受动板被使动板推动(图7右),而不是拉动(图7左)。至此,要构建一个非门就很简单了,只需数据位处于0时闭合、1时断开的开关(如图7底部两张图所示)译者注。
译者注:相当于与图6的逻辑相反。
有了机械继电器,现在可以直接构建余下的逻辑操作了。图8用抽象符号展示了机器中的必备线路。等效的机械装置应该不难设想。
现在谁都可以构建自己的祖思机械计算机了。基础零件就是机械继电器。可以设计更复杂的连接(比如包含两块受动板的继电器),只是相应的机械结构只能用平板和小杆构建。
构建一台完整的计算机的关键难题是把所有部件相互连接起来。注意数据位的移动方向总是与结果位的移动方向正交。每一次完整的逻辑操作都会将机械移动旋转90度。下一次逻辑操作又把移动旋转90度,以此类推。四门之后,回到最初的移动方向。这就是为什么祖思用东南西北作为周期单位。在一个机器周期内,可以运行4层逻辑计算。逻辑门既可简单如非门,也可复杂如包含两块受动板(如XOR)。Z1的时钟表现为,4次衔接内完成一次加法:衔接IV加载参数,衔接I和II计算部分和与进位,衔接III计算最终结果。
输入的数据位在某层上移动,而结果的数据位传到了别层上去。意即,小杆可以在机器的层片之间上下传递比特。我们将在加法线路中看到这一点。
至此,图5的内涵就更丰富了:各单元里的圆圈正是祖思抽象符号里的圆圈,并反映着逻辑门的状态。现在,我们可以从机械层面拔高,站在更逻辑的高度探讨Z1。
Z1的内存
内存是目前我们对Z1理解最透彻的部分。Schweier和Saupe曾于20世纪90年代对其有过介绍[4]。Z4——康拉德·祖思于1945年完成的继电器计算机——使用了一种非常类似的内存。Z4的处理器由电话继电器构建,但其内存仍是机械式的,与Z1相似。如今,Z4的机械式内存收藏于德意志博物馆。在一名学生的辅助下,我们在计算机中仿真出了它的运作。
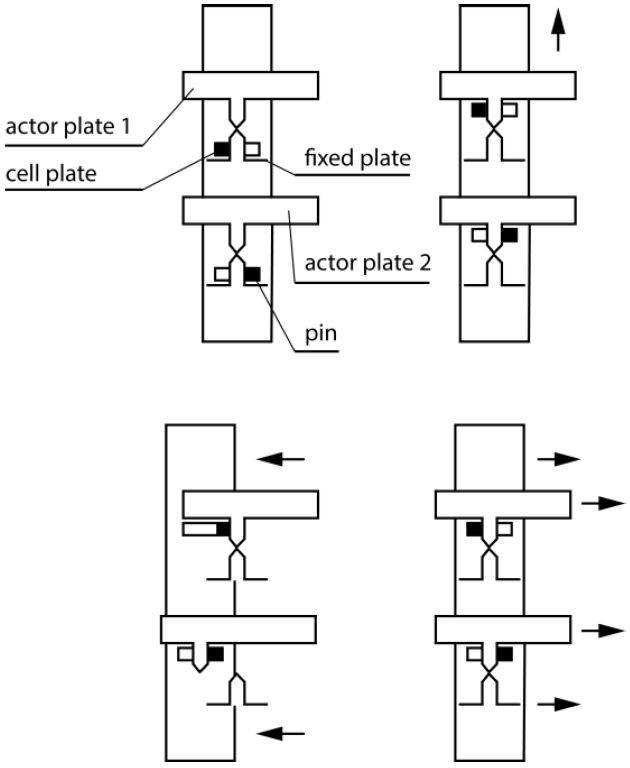
Z1中数据存储的主要概念,就是用垂直的销钉的两个位置来表示比特。一个位置表示0,另一个位置表示1。下图展示了如何通过在两个位置之间来回移动销钉来设置比特值。
图9(a)译者注展示了内存中的两个比特。在步骤9(b)中,纵向的控制板带着销钉上移。步骤9(c)中,两块横向的使动板中,下侧那块被销钉和控制板推动,上侧那块没被推动。步骤9(d)中,比特位移回到初始位置,而后控制板将它们移到9(a)的位置。从这样的内存中读取比特的过程具有破坏性。读取一位之后,必须靠9(d)的回移还原比特。
译者注:作者没有在图中标出abcd,左上为(a),右上为(b),左下为(c),右下为(d)。另,这组插图有点抽象,我也是盯了好久才看懂,它是俯视图,黑色的小正方形是销钉,纵向的长方形是控制板,销钉在控制板上的长方形洞里移动(两个位置表示0和1),横向的两块带尖齿的长方形是使动板。
通过解码6位地址,寻址字。3位标识8个层片,另外3位标识8个字。每一层的解码线路是一棵典型的三层继电器二进制树,这和Z3中一样(只是树的层数不同)。
我们不再深究机械式内存的结构。更多细节可参见文献[4]。
Z1的加法单元
战后,康拉德·祖思在一份文档里介绍过加法单元,但Z1复制品中的加法单元与之不同。那份文档[6]中,使用OR、AND和恒等(NOT-XOR)逻辑门处理二进制位。而Z1复制品中,加法单元使用两个XOR和一个AND。
前两步计算是:a) 待相加的两个寄存器按位XOR,保存结果;b) 待相加的两个寄存器按位AND,保存结果。第三步就是根据前两步计算进位。进位设好之后,最后一步就是对进位和第一步XOR的结果进行按位XOR运算。
下面的例子展示了如何用上述步骤完成两数的二进制相加。
康拉德·祖思发明的计算机都使用了「预进位」。比起在各二进制位之间串行地传递进位,所有位上的进位可以一步完成。上面的例子就说明了这一过程。第一次XOR产生不考虑进位情况下两个寄存器之和的中间结果。AND运算产生进位比特:进位要传到左边的比特上去,只要这个比特在前一步XOR运算结果是1,进位将继续向左传递。在示例中,AND运算产生的最低位上的进位造成了三次进位,最后和第一次XOR的结果进行XOR。XOR运算产生的一列连续的1犹如火车头,牵引着AND所产生的进位,直到1的链条断裂。
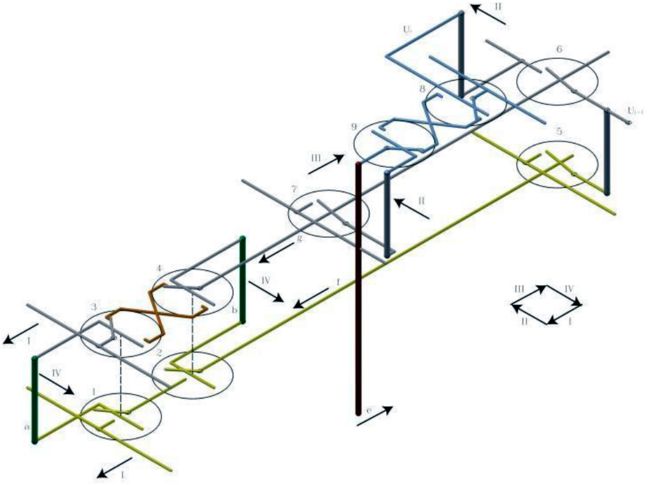
图10所示就是Z1复制品中的加法线路。图中展示了a杆和b杆这两个比特的相加(假设a是寄存器Aa中的第i个比特,b是寄存器Ab中的第i个比特)。使用二进制门1、2、3、4并行进行XOR和AND运算。AND运算作用于5,产生进位ui+1,与此同时,XOR运算用6闭合XOR的比特「链」,或让它保持断开。7是将XOR的结果传给上层的辅助门。8和9计算最后一步XOR,完成整个加法。
箭头标明了各部件的移动。4个方向都上阵了,意即,一次加法运算,从操作数的加载到结果的生成,需要一整个周期。结果传递到e杆——寄存器Ae的第i位。
加法线路位于加法区域的第1、2、3个层片(如后头的图13所示)。康拉德·祖思在没有正式受过二进制逻辑学培训的情况下,就整出了预进位,实在了不得。连第一台大型电子计算机ENIAC采用的都只是十进制累加器的串行进位。哈佛的Mark I用了预进位,但是十进制。
5 Z1的序列器
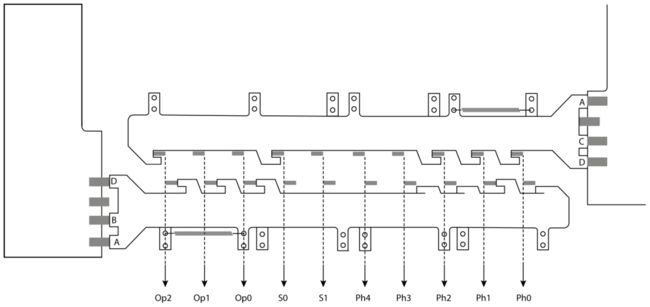
Z1中的每一项操作都可以分解为一系列微指令。其过程根据一种叫做「准则(criteria)」的表格实现,如图11所示,表格由成对放置的108块金属板组成(在此我们只能看到最顶上——即层片12——的一对板。剩下的位于这两块板下面,合共12层)。用10个比特编排表格中的条目(金属板本身):
- 比特Op0、Op1和Op2是指令的二进制操作码
- 比特S0和S1是条件位,由机器的其他部分设置。举个例子,当S0=1时,加法就转换成了减法。
- 比特Ph0、Ph1、Ph2、Ph3、Ph4用于对一条指令中的微周期(或者说「阶段」)计数。比如,乘法运算消耗20个阶段,于是Ph0~Ph4这五个比特在运算过程中从0增长到19。
这10个比特意味着,理论上我们可以定义多达1024种不同的条件或者说情况。一条指令最多可占32个阶段。这10个比特(操作码、条件位、阶段)推动金属销(图11中涂灰者),这些金属销hold住微控制板以防它们弹到左边或右边(如图所示,每块板都连着弹簧)。微控制板上分布着各异的齿,这些齿决定着以当前10根控制销的位置,是否可以阻止板的弹动。每块控制板都有个「地址」。当这10位控制比特指定了某块板的地址,它便可以弹到右边(针对图11中上侧的板)或左边(针对图11中下侧的板)。
控制板弹到右侧会按到4个条件位(A、B、C、D)。金属板根据相应准则切割,从而按下A、B、C、D不同的组合。
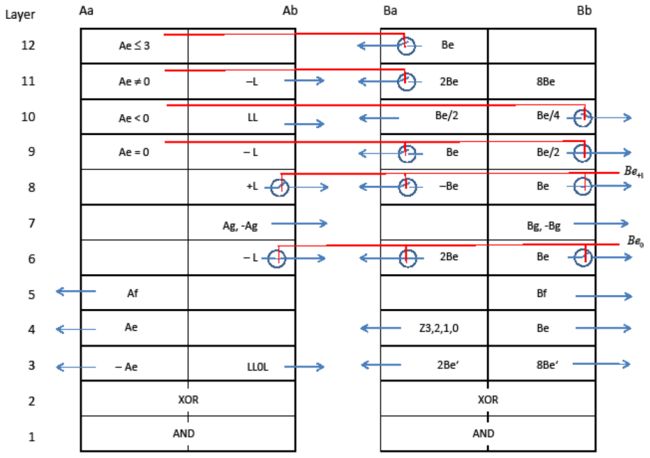
由于这些板分布于机器的12个层片上, 激活一块控制板自然也意味着为下一步的操作选好了相应的层片。指数单元中的微操作可以和尾数单元的微操作并行开始,毕竟两块板可以同时弹动:一块向左,一块向右。其实也可以让两个不同层片上的板同时朝右弹(右侧对应尾数控制),但机械上的局限限制了这样的「并行」。
因此控制Z1,就相当于调整金属板上的齿,以使它们可以响应具体的10比特组合,去作用到左右侧的单元上。左侧控制着处理器的指数部分。右侧控制着尾数部分。选项A、B、C、D是互斥的,意即,微控制板只选其一(就是唯一不被按下的那个)。
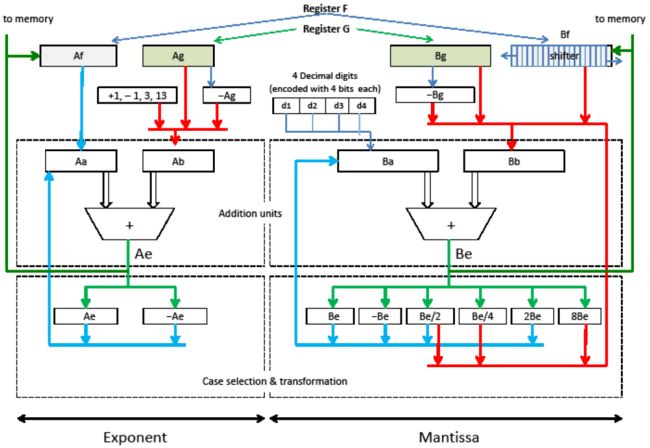
6 处理器的数据通路
图12展示了Z1的浮点数处理器。处理器分别有一条处理指数(图左)和一条处理尾数(图右)的数据通路。浮点型寄存器F和G均由记录指数的7个比特和记录尾数的17个比特构成。指数-尾数对(Af,Bf)是浮点寄存器F,(Ag,Bg)是浮点寄存器G。参数的符号由外部的一个符号单元处理。乘除结果的符号在计算前得出。加减结果的符号在计算后得出。
我们可以从图12中看到寄存器F和G,以及它们与处理器其他部分的关系。ALU(算术逻辑单元)包含着两个浮点寄存器:(Aa,Ba)和(Ab,Bb)。它们直接就是ALU的输入,用于加载数值,还可以根据ALU的输出Ae和Be的总线反馈,保存迭代过程中的中间结果。
Z1中的数据总线使用「三态」模式,意即,诸多输入都可以推到同一根数据线(也是个机械部件)上。不需要「用电」把数据线和输入分离开来,因为根本也没有电。因着机械部件没有移动(没有推动)就代表输入0,移动(推动)了就代表输入1,部件之间不存在冲突。如果有两个部件同时往一根数据线上输入,唯一重要的是确保它们能根据机器周期按序执行(推动只在一个方向上生效)。
程序员能接触到的寄存器只有(Af,Bf)和(Ag,Bg)。它们没有地址:加载指令第一个加载的寄存器是(Af,Bf),第二个加载的是(Ag,Bg)。加载完两个寄存器,就可以开始算术运算了。(Af,Bf)同时还是算术运算的结果寄存器。(Ag,Bg)在一次算术运算之后可以隐式加载,并继续担当新一轮算术运算的第二个参数。这种寄存器的使用方案和Z3相同。但Z3中少了(Ag,Bg)。其主寄存器和辅寄存器之间的协作比Z1更复杂。
从处理器的数据通路可见,独立的寄存器Aa、Ab、Ba和Bb可以加载不同类型的数据:来自其他寄存器的值、常数(+1、-1、3、13)、其他寄存器的取负值、ALU反馈回来的值。可以对ALU的输出进行取负值或移位操作。以代表与2n相乘的矩形框表示左移n位;以与2n相除表示右移n位。这些矩形框代表具有相应的移位或求补逻辑的机械线路。举个例子,寄存器Ba和Bb相加的结果存于Be,可以对其进行多种转换:可以取反(-Be)、可以右移一或两位(Be/2、Be/4)、或可以左移一或三位(2Be、8Be)。每一种转换都在组成ALU的机械层片中有着各自对应的层片。有效计算的相关结果将传回给寄存器Ba或Bb。具体是哪个寄存器,由微控制器指定的、激活相应层片的小杆来指定。计算结果Be也可以直接传至内存单元(图12没有画出相应总线)。
ALU在每个周期内都进行一次加法。ALU算完后,擦除各寄存器Aa、Ab、Ba、Bb,可载入反馈值。
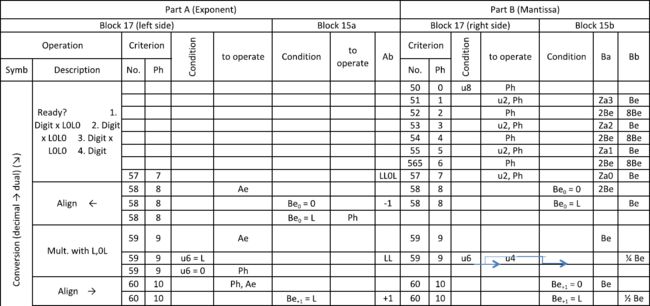
寄存器Ba有一项特殊使命,就是将四位十进制的数转换成二进制。十进制数从机械面板输入,每一位都转换成4个比特。把这些4比特的组合直接传进Ba(2-13的位置),将第一组4比特与10相乘,下一组与这个中间结果相加,再与10相乘,以此类推。举个例子,假设我们想转换8743这个数,先输入8并乘以10。然后7与这个结果相加,所得总数(87)乘以10。4再与结果(870)相加,以此类推。如此实现了一种将十进制输入转换为二进制数的简单算法。在这一过程中,处理器的指数部分不断调整最终浮点结果的指数。(指数ALU中常数13对应213,后文还有对十-二进制转换算法的详述。)
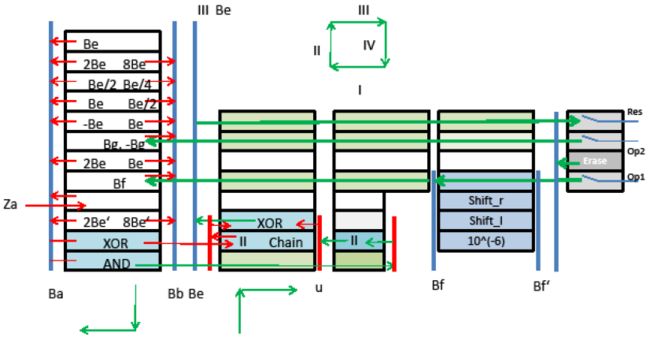
图13还展示了处理器中,尾数部分数据通路各零件的空间分布。机器最左侧的模块由分布在12个层片上的移位器构成。寄存器Bf和Bg(层片5和层片7)直接从右边的内存获得数据。寄存器Be中的结果横穿层片8回传至内存。寄存器Ba、Bb和Be靠垂直的小杆存储比特值(在上面这幅处理器的横截面图中只能看到一个比特)。ALU分布在两摞机械上。层片1和层片2完成对Ba和Bb的AND运算和XOR运算。所得结果往右传,右边负责完成进位以及最后一步XOR运算,并把结果存储于Be。结果Be可以回传、存进内存,也可以以图中的各方式进行移位,并根据要求回传给Ba或Bb。有些线路看起来多余(比如将Be载入Ba有两种方式),但它们是在提供更多的选择。层片12无条件地将Be载入Ba,层片9则仅在指数Ae为0时才这么做。图中,标成绿色的矩形框表示空层片,不承担计算任务,任由机械部件穿堂而过。Bf和Bf'之间的矩形框包含了Bf做乘法运算时所需的移位器(处理时Bf中的比特从最低一位开始逐位读入)。
现在你可以想象出这台机器里的计算流程了:数据从寄存器F和G流入机器,填入寄存器A和B。执行一次加法或一系列的加减(以实现乘除)运算。在A和B中不断迭代中间结果直至得到最终结果。最终结果载入寄存器F,而后开始新一轮的计算。
7 算术指令
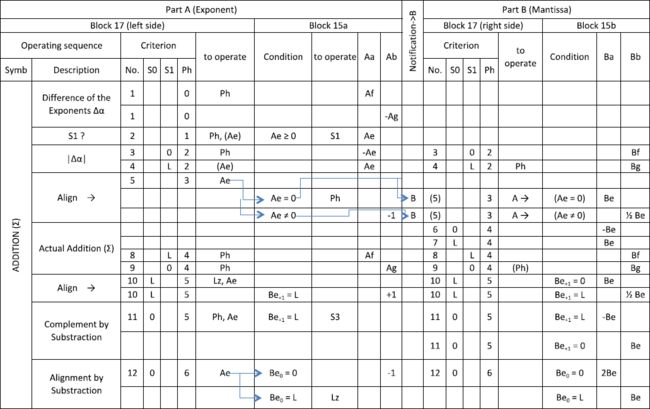
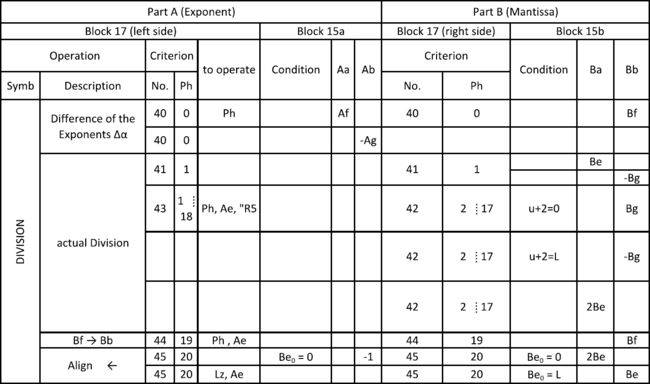
前文提过,Z1可以进行四则运算。在下面将要讨论的表格中,约定用字母「L」表示二进制的1。表格给出了每一项操作所需的一系列微指令,以及在它们的作用下处理器中寄存器之间的数据流。一张表总结了加法和减法(用2的补数),一张表总结了乘法,还有一张表总结了除法。关于两种I/O操作,也有一张表:十-二进制转换和二-十进制转换。表格分为负责指数的A部分和负责尾数的B部分。表中各行显示了寄存器Aa、Ab、Ba、Bb的加载。操作所对应的阶段,在标「Ph」的列中给出。条件(Condition)可以在开始时触发或禁用某操作。某一行在执行时,增量器会设置条件位,或者计算下一个阶段(Ph)。
加法/减法
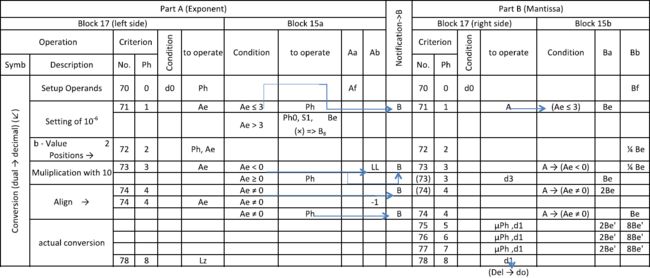
下面的微指令表,既涵盖了加法的情况,也涵盖了减法。这两种操作的关键在于,将参与加减的两个数进行缩放,以使其二进制指数相等。假设相加的两个数为m1×2a和m2×2b。如果a=b,两个尾数就可以直接相加。如果a>b,则较小的那个数就得重写为m2×2b-a×2a。第一次相乘,相当于将尾数m2右移(a-b)位(使尾数缩小)。让我们就设m2'=m2×2b-a。相加的两个数就变成了m1和m2'。共同的二进制指数为2a。a 译者注:原文写的是「cycle」,即周期,下文也有用「phase」(阶段)的,根据表中信息,统一用「Ph」更直观,下同。 表中(图15),先找出两数中较大的二进制指数,而后,较小数的尾数右移一定位数,至两者的二进制指数相等。真正的相加从Ph4开始,由ALU在一个Ph内完成。Ph5中,检测这一结果尾数是否是规格化的,如果不是,则通过移位将其规格化。(在进行减法之后)有可能出现结果尾数为负的情况,就将该结果取负,负负得正。条件位S3记录着这一符号的改变,以便于为最终结果进行必要的符号调整。最后,得到规格化的结果。 穿孔带读取器附近的符号单元(见图5,区域16)会预先计算结果的符号以及运算的类型。如果我们假设尾数x和y都是正的,那么对于加减法,(在分配好符号之后)就有如下四种情况。设结果为z: 加法执行如下步骤: 译者注:原文写的是左移,根据上下文,应为右移,暂且视为作者笔误,下文减法步骤中同。 译者注:原文写的是「D」,但表中用的是「∆α」,遂纠正,下同。我猜作者在输了一遍「∆α」之后觉得麻烦,打算完稿之后统一替换,结果忘了……全文有不少此类不够严谨的细节,大抵是由于没有正式发表的缘故。 减法执行如下步骤: 符号单元预先算得了符号,最终结果的符号需要与它结合得出。 乘法 对于乘法,首先在Ph0,两数的指数相加(准则21,指数部分)。而后耗时17个Ph,从Bf中二进制尾数的最低位检查到最高位(从-16到0)。每一步,寄存器Bf都右移一位。比特位mm记录着之前从-16的位置被移出来的那一位。如果移出来的是1,把Bg加到(之前刚右移了一位的)中间结果上,否则就把0加上去。这一算法如此计算结果: Be = Bf0×20×Bg + Bf-1×2-1×Bg + ··· + Bf-16×2-16×Bg 做完乘法之后,如果尾数大于等于2,就在Ph18中将结果右移一位,使其规格化。Ph19负责将最终结果写到数据总线上。 除法 除法基于所谓的「不恢复余数法」,耗时21个Ph。从最高位到最低位,逐位算得商的各个比特。首先,在Ph0计算指数之差,而后计算尾数的除法。除数的尾数存放在寄存器Bg里,被除数的尾数存放在Bf。Ph0期间,将余数初始化至Bf。而后的每个Ph里,在余数上减去除数。若结果为正,置结果尾数的相应位为1。若结果为负,置结果尾数的相应位为0。如此逐位计算结果的各个位,从位0到位-16。Z1中有一种机制,可以按需对寄存器Bf进行逐位设置。 如果余数为负,有两种对付策略。在「恢复余数法」中,把除数D加回到余数(R-D)上,从而重新得到正的余数R。而后余数左移一位(相当于除数右移一位),算法继续。在「不恢复余数法」中,余数R-D左移一位,加上除数D。由于前一步中的R-D是负的,左移使他扩大到2R-2D。此时加上除数,得2R-D,相当于R左移之后与D的差,算法得以继续。重复这一步骤直至余数为正,之后我们就又可以减去除数D了。在下表中,u+2表示二进制幂中,位置2那儿的进位。若此位为1,说明加法的结果为负(2的补数算法)。 不恢复余数法是一种计算两个浮点型尾数之商的优雅算法,它省去了存储的步骤(一个加法Ph的时耗)。 译者注:原文写的是除数在Bf、被除数在Bg,又是一处明显的笔误。 奇怪的是,Z3在做除法时,会先测试Ba和Bb之差是否可能为负,若为负,就走Ba到Be的一条捷径总线使减去的除数无效(丢弃这一结果)。复制品没有使用这一方法,不恢复余数法比它优雅得多。 输入控制台由4列、每列10块小盘构成。操作员可以在每一列(从左至右分别为Za3、Za2、Za1、Za0)上拨出数字0~9。意即,能输入任意的四位十进制数。每拨一位数,便相应生成等效的、4比特长的二进制值。因而,该输入控制台相当于一张4×10的表,存着10个0~9的二进制值。 而后Z1的处理器负责将各十进制位Za3、Za2、Za1、Za0通过寄存器Ba(在Ba-13的位置,对应幂2-13)传到数据通路上。先输入Za3(到寄存器Ba),乘以10。再输入Za2,再乘以10。四个位,皆如是重复。Ph7过后,4位十进制数的二进制等效值就在Be中诞生了。Ph8,如有需要,将尾数规格化。Ph7将常数13(二进制是LL0L)加到指数上,以确保在尾数-13的位置上输入数。 用一根小杆设置十进制的指数。Ph9中,这根小杆所处的位置代表了输入时要乘多少次10。 图19中的表展示了如何将寄存器Bf中的二进制数转换成在输出面板上显示的十进制数。 为免遇到要处理负十进制指数的情况,先给寄存器Bf中的数乘上10-6(祖思限制了机器只能操作大于10-6的结果,即便ALU中的中间结果可以更小些)。这在Ph1完成。这一乘法由Z1的乘法运算完成,整个过程中,二-十进制译者注转换保持「挂起」。 译者注:原文写的十-二进制,目测笔误。 此后,尾数右移两位(以使二进制小数点的左边有4个比特)。尾数持续位移,直到指数为正,乘3次10。每乘一次,把尾数的整数部分拷贝出来(4个比特),把它从尾数里删去,并根据一张表(Ph4~7中的2Be'-8Be'操作)转换成十进制的形式。各个十进制位(从最高位开始)显示到输出面板上。每乘一次10,十进制显示中的指数箭头就左移一格位置。译者注 译者注:说实话这一段没完全看懂,翻译可能与原意有出入。 Z1的原型机毁于1943年12月柏林一场盟军的空袭中。如今已不可能判定Z1的复制品是否和原型一样。从幸存的那些照片上看,原型机是个大块头,而且不那么「规则」。此处我们只能相信祖思本人所言。但我觉得,尽管他没什么理由要在重建的过程中有意识地去「润色」Z1,记忆却可能悄悄动着手脚。祖思在1935~1938年间记下的那些笔记看起来与后来的复制品一致。据他所言,1941建成的Z3和Z1在设计上十分相似。 20世纪80年代,西门子(收购了祖思的计算机公司)为重建Z1提供了资金。在两名学生的辅助下,祖思在自己家中完成了所有的建造工作。建成之后,为方便起重机把机器吊起来,运送至柏林,结果祖思家楼上拆掉了一部分墙。 重建的Z1是台优雅的计算机,由成千上万的部件组成,但并没有多余。比如尾数ALU的输出可以仅由两个移位器实现,但祖思设置的那些移位器明显以较低的代价提升了算术运算的速率。我甚至发现,Z1的处理器比Z3的更优雅,它更简洁,更「原始」。祖思似乎是在采用了更简单、更可靠的电话继电器之后,反而在CPU的尺寸上「铺张浪费」。同样的事也发生在Z3若干年后的Z4身上。Z4根本就是大版的Z3,有着大版的指令集,而计算机架构是基本一样的,就算它的指令更多。机械式的Z1从未能一直正常运行,祖思本人后来也称之为「一条死胡同」。他曾开玩笑说,1989年Z1的复制品那是相当精确,因为原型机其实不可靠,虽然复制品也可靠不到哪去。可神奇的是,Z4为了节省继电器而使用的机械式内存却非常可靠。1950~1955年间,Z4在瑞士的苏黎世联邦理工学院(ETH Zürich)服役,其机械内存运行良好[7]。 最令我惊讶的是,康拉德·祖思是何等年轻,就对计算机引擎给出了如此优雅的设计。在美国,ENIAC或MARK I团队都是由经验丰富的科学家和电子专家组成的,与此相反,祖思的工作孤立无援,他还没有什么实际经验。从架构上看,我们今天的计算机进与1938年的祖思机一致,反而与1945年的ENIAC不同。直到后来的EDVAC报告草案,以及冯·诺依曼和图灵开发的位串行机中,才引进了更优雅的体系结构。约翰·冯·诺依曼(John von Neumann)1926~1929年间居于柏林,是柏林大学最年轻的讲师(报酬直接来自学生学费的无薪大学教师)。那些年,康拉德·祖思和冯·诺依曼许能在不经意间相遇相知。在那疯狂席卷、那黑夜笼罩德国之前,柏林本该有着许多的可能。 [1] Horst Materna, Die Geschichte der Henschel Flugzeug-Werke in Schönefeld bei Berlin 1933-1945, Verlag Rockstuhl, Bad Langensalza, 2010.
对于情况(1)和(4),可由ALU中的加法来处理。情况(1)中,结果为正。情况(4),结果为负。情况(2)和(3)需要做减法。减法的符号在Ph5(图15)中算得。
8 输入和输出
9 总结
参考文献
[2] Zuse, K., Der Computer – Mein Lebenswerk, Springer-Verlag, Berlin, 3rd Edition, 1993.
[3] Rojas, R., "Konrad Zuse's legacy: the architecture of the Z1 and Z3", Annals of the History of Computing, Vol. 19, N. 2, 1997, pp. 5–16.
[4] Ursula Schweier, Dietmar Saupe, "Funktions- und Konstruktionsprinzipien der programmgesteuerten mechanischen Rechenmaschine Z1", Arbeitspapiere der GMD 321, GMD, Sankt Augustin, August 1998.
[5] Rojas, R. (ed.), Die Rechenmaschinen von Konrad Zuse, Springer-Verlag, Berlin, 1998.
[5] Website: Architecture and Simulation of the Z1 Computer, http: http://zuse-z1.zib.de/, last access: July 21st, 2013.
[6] Konrad Zuse, "Rechenvorrichtung aus mechanischen Schaltglieder", Zuse Papers, GMD 019/003 (undated), http://zuse.zib.de/, last access July 21st, 2013.
[7] Bruderer, H.: Konrad Zuse und die Schweiz: Wer hat den Computer erfunden?, Oldenbourg Wissenschaftsverlag, Munich, 2012.
[8] Goldstine, H.: "The Electronic Numerical Integrator and Computer (ENIAC)", Annals of the History of Computing, Vol. 18 , N. 1, 1996, S. 10–16.